基于陀螺仪转角传感器的动态信号测量及物理参数时域识别
周云,曾雅丽思,赵瑜,易伟建1,
(1.工程结构损伤诊断湖南省重点实验室,湖南 长沙 410082;2.湖南大学 土木工程学院,湖南 长沙 410082;3.绿色先进土木工程材料及应用技术湖南省重点实验室,湖南 长沙 410082)
系统识别方法始于20 世纪70 年代,引入土木工程领域已有近40 余年的发展历史[1].该方法是工程结构损伤诊断和状态评估的重要手段,它可以从建筑物动力响应中识别出结构的当前状态.结构的性态通常用结构模态参数(主要为自振频率和振型)和结构物理参数(主要为刚度参数)来描述.结构物理参数的变化相比模态参数的变化更为直观地反映了结构状态的改变[2].进行结构物理参数识别的方法,主要分为频域识别和时域识别两种,与频域识别方法相比,时域识别更加直接,实测的时程数据中的结构信息更加丰富,且增加时程响应采样点数可以有效增加时域识别方程的个数[3].目前制约时域识别应用于实际工程中的一个主要原因是结构响应信息不完备,通常时域方程中主要使用位移类信息,转角类信息很难测试得到,往往只能测量结构的一个状态量,加速度、速度或位移响应的一种,而且转角信息难以准确测量.如何在测量信息有限的情况下识别参数以及如何进行信息不完备情况下的识别问题是研究重点之一[4].
为了解决这些问题,众多学者展开了相关研究.扩展卡尔曼滤波[5]方法可以求解响应信息不完备下的结构参数识别问题,但结构参数的识别精度低,甚至会出现参数发散现象.传统方法主要通过重构技术解决时域识别时测量信息的不完备问题.平动信息不完备的处理方法如下:Li 等[6]在获得系统的位移响应后,通过采用微分算子变换方法求得速度与加速度响应,完成系统的参数识别.李国强等[2]采用积分算子变换方法,实现了在无需初速度信息的情况下,由加速度响应重建位移、速度响应.转动信息的计算问题主要采用静力凝聚法[2]和广义逆方法[7]通过水平位移测量值重构转动信息,前者需要预先知道结构的参数信息,而后者不需要,但是两种方法计算效果近似,因此广义逆方法更具适用性.此外,赵昕等[8]采用一组正交基函数对梁式构件的平动反应曲线进行拟合,从而获得其转角响应信息.
关于测量动态旋转角度的研究不多,主要是因为转动响应的最大振幅通常在毫弧度范围以内,所以要求仪器必须非常灵敏,而且需对测量的运动以外的其他运动非常不敏感[9].通过文献调研发现,Ewins 等[10]在文献中对转角自由度间接测量方法进行了详细的分类介绍.包括采用附加T 模块法[11]、激光多普勒测振仪[12]、激光位移计[13]等测量转角,但这些测量方法和设备过于复杂,难以运用于自由度较多的情况.Lee 等[14]采用商用相机和低成本的帧捕获器,利用事先标定参数的图像处理技术,测量了五层试验塔在激振器下的角度响应.然而,摄像机的方法需要额外的计算图像处理,如像素扫描、目标识别和轮廓定义,实际应用并不方便.也有学者尝试采用应变推算转角,Xia 等[15]通过在广州塔上安装振动应变仪,利用实时监测的应变数据计算弯曲梁型结构顶部的倾斜角度,Dimsdale[9]采用在杆件两端粘贴应变片的方式间接计算杆件两端的弯曲转角,该方法的应用前提是与其他杆件的连接方式不影响杆件的相对转动.测量转角自由度的传感器技术远不如测量位移自由度的传感器成熟,目前采用较多的是倾角仪和陀螺仪,Hou 等[16]利用MEMS 倾角仪监测钢筋混凝土柱在地震荷载作用下的结构旋转角,该传感器对被测物体的振动频率非常敏感,仅适用于1 Hz以内的外激励频率.倾角仪适合低频的振动,而陀螺仪在高频振动下的性能更为稳定,是测量动态角度的理想传感器.
由于转角响应难以获得,目前结构识别算法的研究主要集中于剪切型结构和桁架结构[17-18],而以弯剪变形为主的结构研究较少.弯剪型结构在正问题分析中通常利用静力凝聚的方法缩聚掉转角自由度,在反问题求解过程中,主要利用平动响应重构转动响应.目前关于如何通过直接测量得到动态角度信息的研究十分有限,测量转角自由度的传感器价格也普遍较高,不适合大量应用于工程结构中.在时域识别方面,传统算法在重构状态信息以及广义逆求转角时,计算模型所使用的方程式存在对冲效应,需要应用超定方程组修正结果,方法过于复杂且精度不能完全满足要求.因此本文以一座4 层框架结构为例,在对该结构进行转动信息重构的前提下,基于最小二乘递推算法由结构的平动响应数据在时域内识别了结构的物理参数.对比运用转动响应真实值的情形下所识别的物理参数,研究使用转角重构值对结构物理参数时域识别的影响.为获得准确的转角测量值,本文利用MEMS 陀螺仪传感器,依据由平动响应信息拟合转动响应的原理,对其在受到冲击振动下的动态精度进行了试验验证.在此基础上,通过一个3 层2 跨的钢框架模型的动力试验,比较了采用广义逆方法重构转角和直接测量转角两种情况下,阻尼参数和刚度参数的识别效果.
1 MEMS 陀螺仪传感器简介
陀螺仪是一种可以用来测量被测物体相对于惯性空间的角速度和角位移的惯性器件.其基本的工作原理为,高速旋转刚体的旋转轴在不受外力影响时,其所指方向不改变.陀螺仪在载体姿态测量方面具有稳定性好、精度高、对环境的适应能力极强等诸多优点,被广泛应用于航空飞行器姿态测量、军事轨迹测量、车辆驾驶控制、数码产品如相机防抖、手机体感操作功能等领域.
MEMS 陀螺仪使用现代的微机电技术,具有体积小、质量轻、成本低、集成度高和精度较高的特点,具有良好的应用前景[19].本文的研究选用的是商业级的MEMS 陀螺仪传感器,深圳维特智能科技的HWT901B 姿态测量传感器,它集成了高精度的陀螺仪、加速度计、地磁场传感器等模块.MEMS 陀螺仪传感器通过采集加速度、角速度以及磁场信号的原始数据,使用高性能的微处理器与卡尔曼动态滤波算法,通过四元数方法解算得到围绕X、Y、Z 轴旋转的俯仰角、偏航角和翻滚角.因此,陀螺仪传感器实际采集的是角速度响应,通过解算才能获得角位移.HWT901B 陀螺仪传感器的性能参数如表1 所示,其采集数据后,通过TTL 电平串口进行数据传输,支持串口数字接口.考虑到实际测量时距离较远,研究团队对其进行改造加入了HC-12 无线收发传输串口通讯模块,整套动态角度测量系统的连接方法如图1 所示.
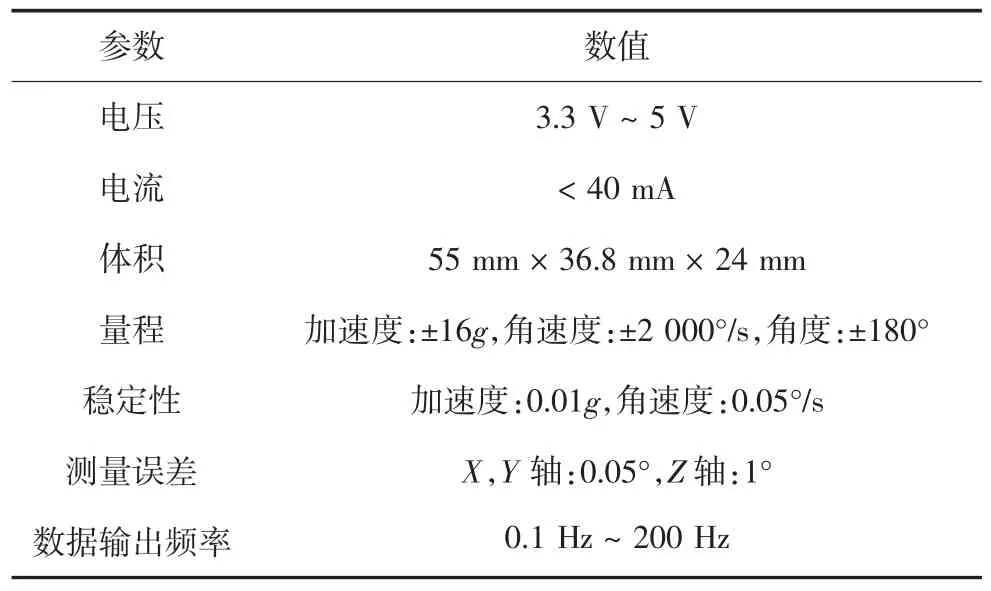
表1 HWT901B 陀螺仪传感器主要参数Tab.1 Main parameters of HWT901B gyroscope sensor

图1 动态角度测量系统Fig.1 Dynamic rotational angle measurement system
2 基于转角拟合的角度测量精度校验
MEMS 陀螺仪传感器体积微小,内部含有多个运动单元,因此其性能对工作环境变化较为敏感.测量过程中的外界冲击振动,环境干扰和自身漂移率都会影响陀螺仪的精度.目前,可通过提高微加工工艺消除尺寸偏差[20]、合理设计优化陀螺仪结构降低耦合误差[21]、建立相应误差模型进行对准[22]、采用数字信号处理技术减小随机噪声的影响[23]等方法来有效提高其精度,HWT901B 正是采用卡尔曼动态滤波算法减少了其漂移误差.考虑到动力试验时,结构将产生高频的往复振动,有必要对MEMS 陀螺仪传感器在受到外界冲击振动下的动态精度进行校验,一般采用陀螺测试转台来检验和评定陀螺仪性能,转台为精密测试设备,一般土木工程应用很少,考虑购买转台或对陀螺仪的精度进行检测的送检价格都过高,受实验条件所限制,故采用了一种角度拟合方法[8]对MEMS 陀螺仪传感器的精度进行了验证,通过对激光位移计实测的结构平动响应曲线拟合得到结构的转动响应曲线.
如图2 所示的等截面梁单元,它联结着两个节点,一般不考虑轴向变形的影响,则该单元在平面内有4 个自由度,包含2 个平动自由度和2 个转动自由度.设有如图3 所示的受到脉冲激励F,跨度为L的欧拉-伯努利梁,其挠度曲线上横坐标为x 的任一点的纵坐标为y,已知t 时刻该梁上n 个测点的平动反应测量值为
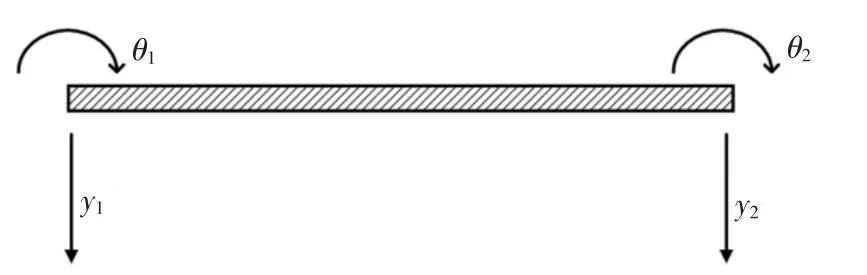
图2 梁单元模型Fig.2 Beam element model

则该时刻n 个测点上的转动变形为平动变形曲线对测点坐标的一阶导数[8]:
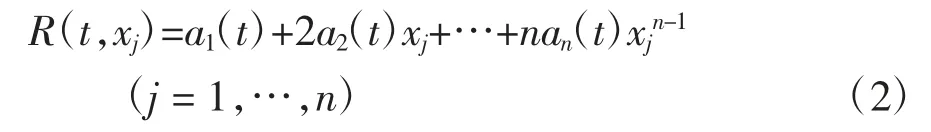
在有限单元法中,梁单元变形曲线为三次多项式,对于荷载作用下的欧拉梁,应当取不低于三次的多项式拟合梁的挠曲线.为求解三次多项式中的4个参数,应至少在梁上布置4 个测点.
根据以上方程可知,只要通过激光位移计测试得到t 时刻4 个测点的位移y1、y2、y3、y4,基于梁单元变形曲线为三次多项式的假定,且已知4 个测点的位置x1、x2、x3、x4,可以拟合得到梁在t 时刻的挠曲线方程(1),求解出a1、a2、a3,将其代入式(2)可求得梁在t 时刻的转角反应,即可计算出t 时刻横坐标为xk处的转角θ.
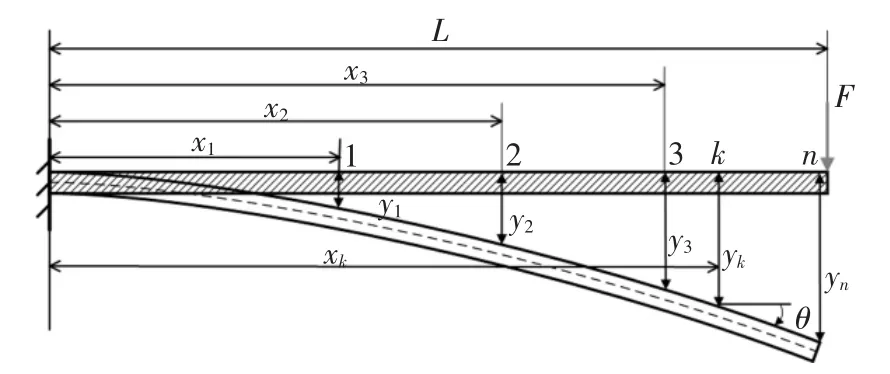
图3 欧拉-伯努利梁模型Fig.3 Euler-Bernoulli beam model
3 基于最小二乘递推算法的结构物理参数时域识别
框架结构是由梁、柱构件组成的结构,可根据横梁与柱的线刚度比值划分为剪切型框架和一般框架结构.若线刚度比值大于5,则在结构分析中,可假定横梁刚度无穷大,忽略梁的变形,视为剪切型结构[24].若框架梁柱的线刚度比值较小,则为一般框架结构.剪切型框架的参数识别已经比较成熟,本文研究对象为一般框架结构,在水平荷载作用下,其框架节点将发生转动,因此需要考虑框架节点转动的影响.
如图4(a)所示的完整自由度模型一,对于钢框架结构的梁柱连接节点,节点的轴向变形和剪切变形与它的转动变形相比,可以忽略不计,因此框架结构计算模型采用梁单元的刚度矩阵为4×4 阶矩阵.对于单跨框架结构,由于结构对称,左右两侧的转动响应一致,可将模型一简化为如图4(b)所示的含N 个平动自由度和N 个转动自由度的模型二.对于多跨框架结构,同一层梁柱节点的转角响应并不完全相同,根据实际情况,可将模型一简化为如图4(c)所示的含N 个平动自由度和2 N 个转动自由度的模型三.
在外力f(t)作用下,对于需要考虑节点转动影响的框架结构,动力平衡方程为
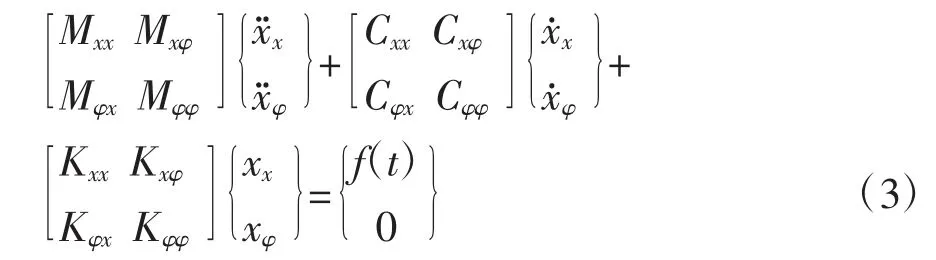
式中:xx、分别为结构的水平位移、速度、加速度响应;xφ、分别为结构的角位移、角速度、角加速度响应;f(t)为外部激励;]分别为协调质量矩阵、阻尼矩阵和刚度矩阵.根据瑞利阻尼假设:C=aM+bK,考虑刚度矩阵的数值的数量级远大于质量矩阵,取a=0,则阻尼矩阵具有与刚度矩阵相同的形式.
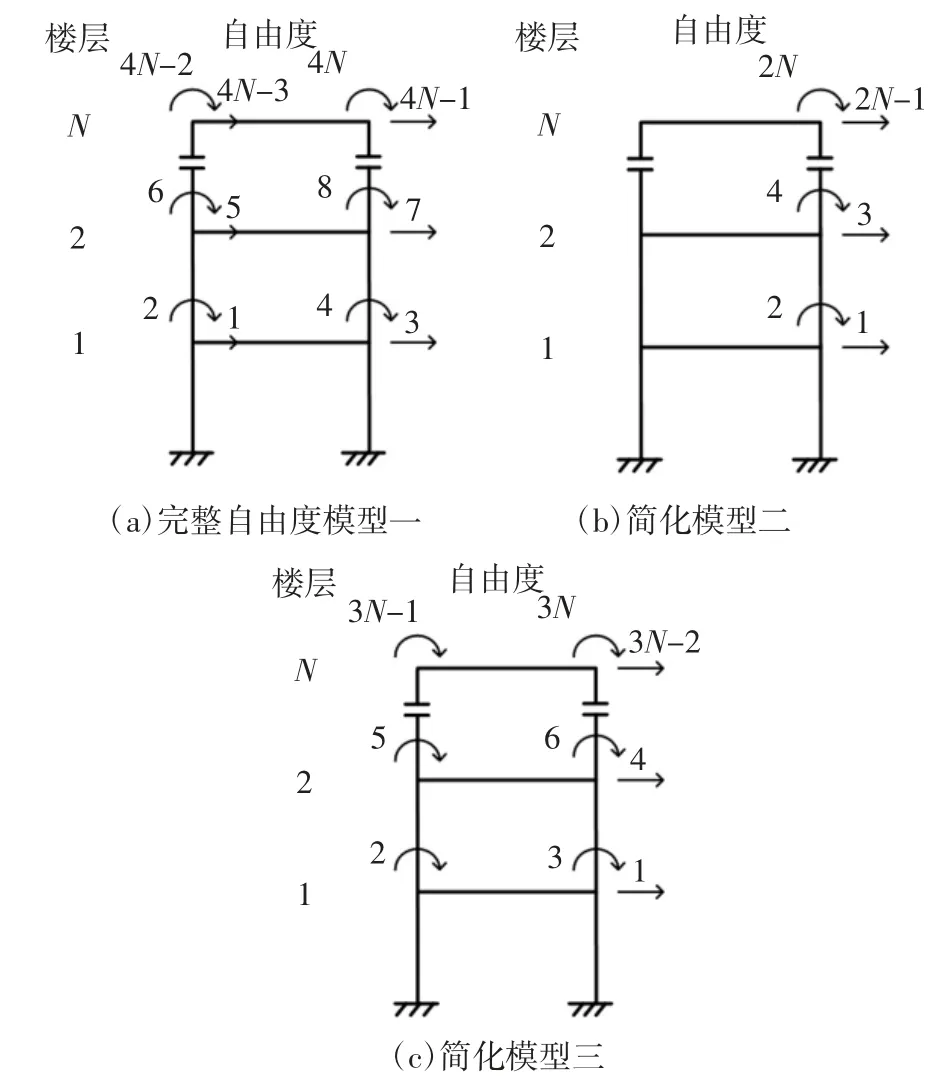
图4 框架结构的计算模型Fig.4 Calculation model of frame structure
假定质量矩阵已知,展开动力平衡方程后有

根据虚拟结构向量转换方法[2],可构造参数识别的标准方程.将式(4)简化为:
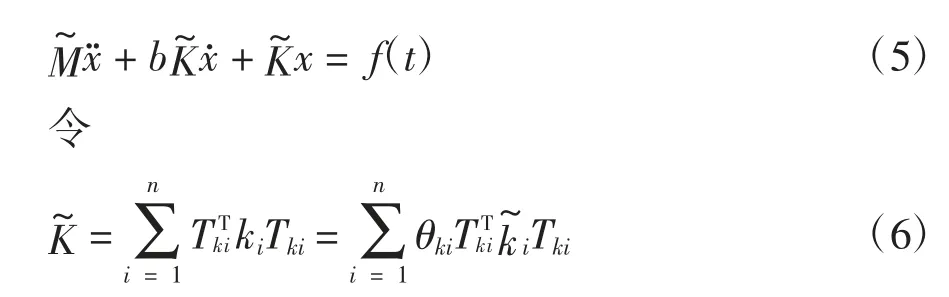
式(6)中,Tki为定位矩阵,ki为局部坐标下的单元刚度矩阵,θki为待识别的刚度参数,为提取公因子θki之后的单刚矩阵.
引入Rki=
则有

式中:
Hk=[Rk1,Rk2,…,Rkn],θk=[θk1,θk2,…,θkn]T
类似地,对于阻尼矩阵有

对于协调质量矩阵有

式中:
Hm=[Rm1,Rm2,…,Rmn],θm=[θm1,θm2,…,θmn]T
而Rmi=
以上所述表达式中,θmi为第i 个单元的质量,为标准化单元质量矩阵.
将式(7)、式(8)、式(9)代入式(5),并引入H=[Hm,Hc,Hk],θ=[θm,θc,θk]T,Z=f(t),即可写成如下的参数识别标准格式:

式中:H 为结构响应矩阵,θ 为待识别的参数向量,Z为系统输入.假定结构系统的输入及输出信息完备,基于最小二乘准则,可得式(10)中的结构参数θ 的估计值为

上述论述表明:利用系统的输入、输出响应信息可以得到结构的物理参数估计值.
3.1 无转角测量值的求解——结构的转角信息重构
以相对简单的单跨框架结构为例说明,在没有任何实测的转动信息的基础上,为了进行式(11)的计算,可采用广义逆理论由水平位移测量值计算转角,计算模型选取模型二.
将式(3)进一步展开后得

假设转角的方向上的惯性力和阻尼力的作用忽略不计,则由式(12)可得

解式(13)可得

由于该式中的Kφx和Kφφ包含有待求参数,因此无法直接用来计算转角响应.陈隽[7]在文献中给出了广义逆方法计算转角的公式:
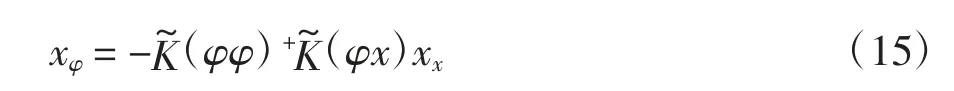
该公式避免了对结构参数的需求.其中:

式中:m=n2,为结构第i 个部分的刚度矩阵的第j 行k 列元素,同理可定义.方程(15)右边的各项均已知,对其两边求一阶导数得
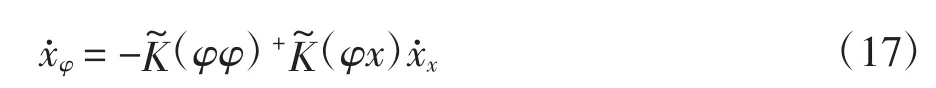
上式为位移-角速度关系式,同理可得位移-角加速度关系式
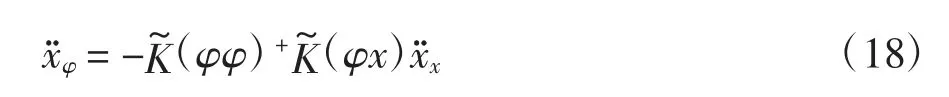
由平动信息重构角度、角速度、角加速度信息后,可进行结构的参数识别.
3.2 有转角测量值的求解
对于可以直接测量转角值的框架结构,同样以模型二为例说明,选取的待识别参数为各层的层抗弯刚度(EI)i和各层的阻尼参数b(EI)i.根据前述理论介绍,可构造如式(10)所示的方程,第i 层和第i+1 层的参数识别方程如下式:
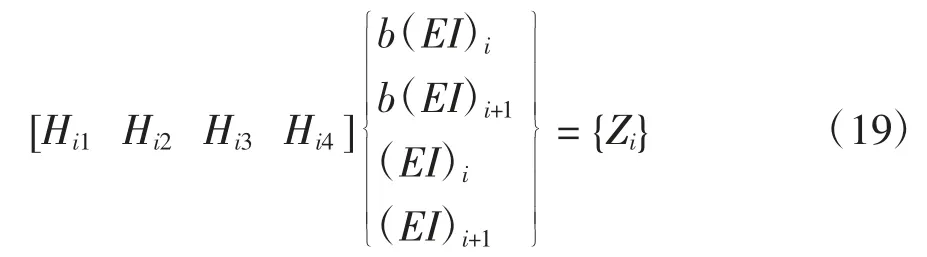
当i >1 时,式中:

式中:hi为第i 层层高.当识别第i=1 层时,
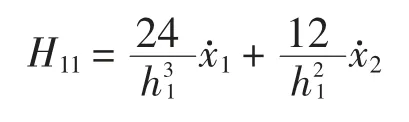
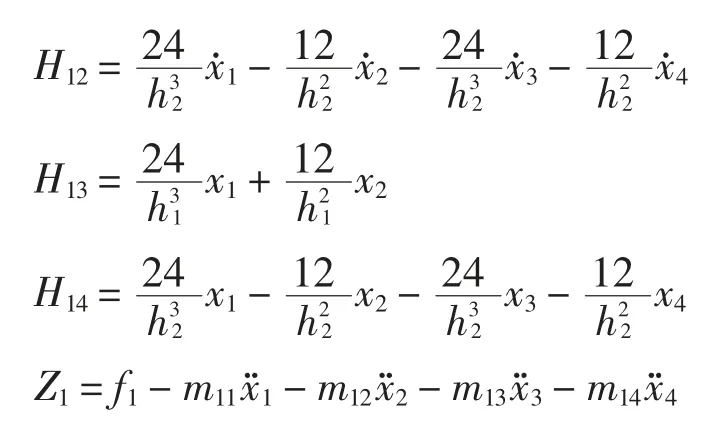
由式(19)可知,已知框架结构的各层层高、质量矩阵、所受外激励以及各节点的平动、转动时程响应,进而建立参数识别标准方程进行最小二乘递推法参数识别,即可求得结构的物理参数.有转角测量值即可省去采用广义逆方法重构转角信息的过程,更为方便.
4 算例分析
以一个4 层弯剪型框架结构为例,在结构左侧顶点水平施加一个大小为100 N 的脉冲力F,采样频率设为200 Hz,共采集12 000 个数据点.计算模型如图5 所示,假设参数如表2 所示.采用Newmark-β时程分析方法进行正问题计算得到结构的动力响应.动力方程中采用与刚度相关的比例阻尼矩阵和协调质量矩阵.采用忽略轴向变形和剪切变形的4×4 阶的杆系单元矩阵,组装成16×16 阶的总刚度矩阵.模型共16 个自由度,由于结构完全对称,可简化为含4个平动自由度和4 个转动自由度的框架模型,则总刚度矩阵变为8×8 阶的矩阵.为了验证算法的抗噪性能,在结构响应分析中分别加入1%、5%的白噪声,加入白噪声的水平由结构响应的均方根值和噪声均方根值的百分比确定.接着使用最小二乘递推算法对1~4 层的层间抗弯刚度K1、K2、K3、K4和各层的刚度阻尼参数C1、C2、C3、C4进行识别.
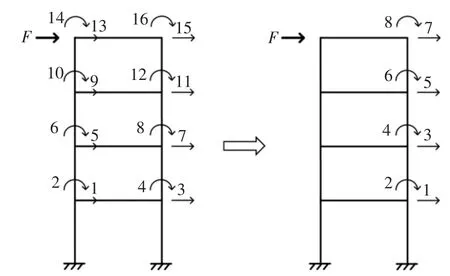
图5 弯剪型框架结构模型Fig.5 Model of shear-bending frame structure
根据实际观测输出信息,设置通过广义逆方法重构转角的工况1 和采用转角真实值的工况2.其中输出的加速度响应和角度、角速度响应都采用真实值.

表2 四层框架结构参数真实值Tab.2 Parameters'real values of four-story frame structure
工况1:采用Newmark-β 积分法计算结构上4个平动自由度的加速度响应,对加速度响应进行傅里叶变换,将信号从时域转换到频域,再通过将时域内的积分转换为频域计算,在频域内进行运算过后再通过傅里叶逆变换将信号从频域还原到时域,并取其实部就可以得到信号在时域的速度和位移响应[25],采用3.1 节所述广义逆方法,根据式(15)(17)和(18)由位移响应重构角度、角速度、角加速度响应.
工况2:基于图5 的计算模型,采用Newmark-β积分法计算结构上4 个平动自由度的加速度响应,4个转动自由度的角度、角速度响应.然后,同工况1 的方法由频域积分法获得速度和位移响应.对角速度响应利用向前差分的数值微分法重构角加速度的响应,初始角速度为0.
获得完备的输入和输出响应信息后,假设结构的待识别参数初值,将以上数据和结构的已知参数代入公式(19)构造结构参数识别方程,根据式(11)运用最小二乘递推算法可求出结构物理参数的识别值,参数识别结果列入表3,图6 为不考虑噪声下,工况1 和工况2 识别结构物理参数的收敛过程.
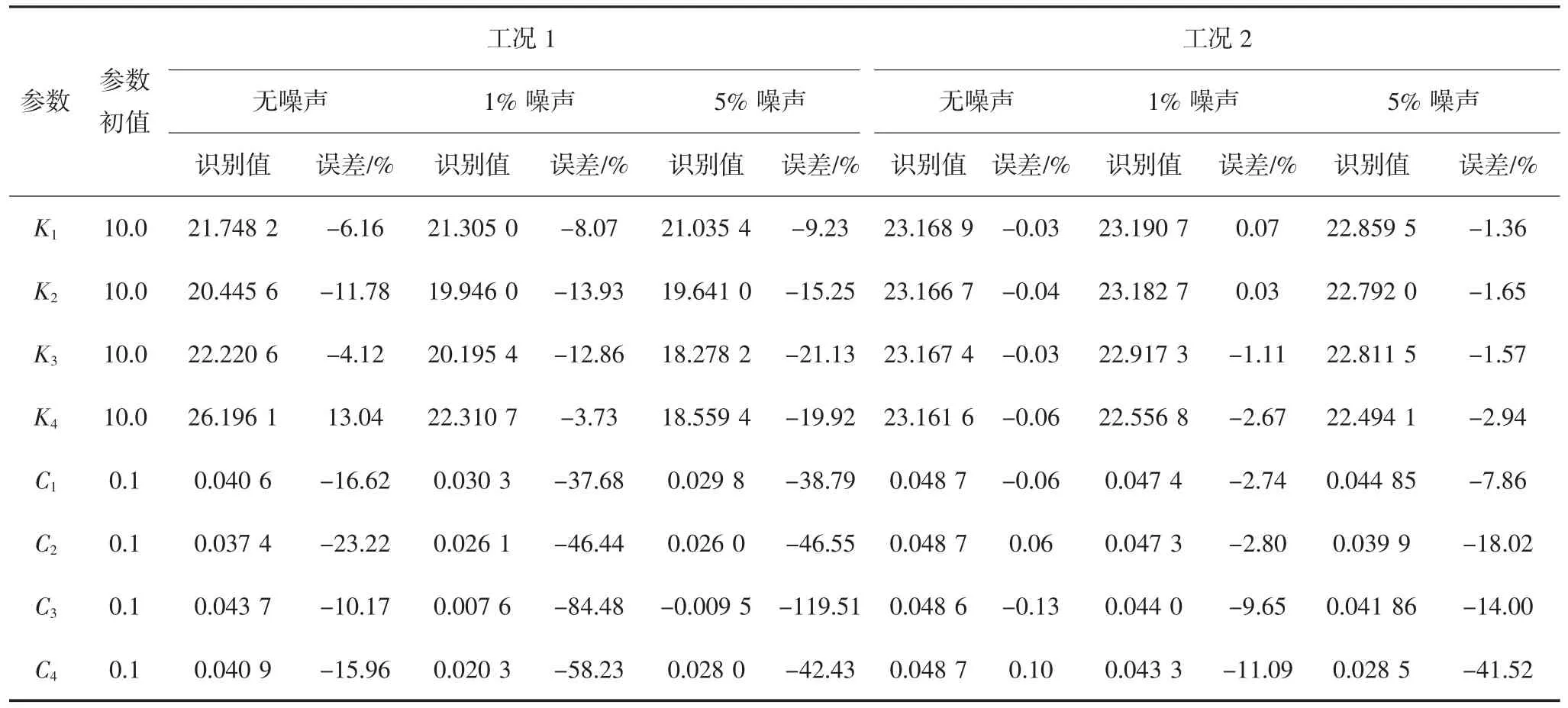
表3 工况1 与工况2 结构物理参数识别结果对比Tab.3 Comparison of identification results of structural physical parameters between case 1 and case 2
比较工况1 和工况2 在无噪声时的结构参数识别结果,可以发现工况1 重构转角响应时刚度参数识别的最大误差为13.04%;而工况2 采用角度和角速度响应真值,识别得到的刚度参数最大误差为0.06%.说明通过广义逆方法由平动响应重构出的角度,角速度和角加速度响应准确度不高,基于最小二乘递推算法进一步进行识别的刚度参数结果也不够理想.从识别的物理量来看,阻尼的识别效果整体要差于刚度参数,考虑噪声后误差更大,阻尼真值很容易被测试噪声所湮没.
考虑5%的噪声存在时,对转角进行重构的工况1 的刚度参数识别最大误差达到21.13%,分析其原因,主要是因为加速度积分成速度和位移产生的误差和广义逆方法本身的误差累积,使得误差进一步放大.考虑5%噪声时,采用角度、角速度真实值的工况2 刚度参数识别的最大误差为2.94%,说明了最小二乘递推算法具有一定的抗噪能力.整体来说,采用重构转角值的工况1 所识别的参数误差较大,因此可以考虑通过传感器直接测量转动响应.

图6 工况1 与工况2 的刚度参数与阻尼参数估计收敛过程Fig.6 Parameter estimation convergence of stiffness and damping parameters for case 1 and case 2
5 试验研究
5.1 MEMS 陀螺仪传感器的角度测量精度验证
有效识别物理参数的前提是保证测量的响应信息准确,因此需对动力试验条件下MEMS 陀螺仪传感器的角度测量精度进行验证.试验结构模型为如图7 所示的门式钢框架结构,选取其右侧柱构件为试验对象.柱尺寸为B×W×L=5 0 mm×3 mm×1 060 mm,角度信号由维特智能HWT901B 陀螺仪传感器采集,共布置2 个MEMS 陀螺仪传感器,位于门式框架右侧柱构件中间位置的传感器用来采集柱的转动响应,左侧柱构件上对称布置的传感器用来保持框架结构质量对称.位移信号由基恩士IL300+IL1000 激光位移计采集,其量程为280 mm,精度为0.7 mm.试验共布置5 个激光位移计,顶端布置1 个用于控制初位移,后4 个以23 cm 为间距等距离布置,用于测量柱的平动响应.试验时,通过左侧绞盘牵引施加2~10 mm 不等的初位移.然后剪断绳子瞬时释放,结构恢复自由振动状态.每隔2 mm 设置一次工况,共5 组试验.由第2 节所述的转动响应曲线拟合方法可以得到激光位移计测得的转动时程响应,与MEMS 陀螺仪传感器测得的转动时程响应结果对比如图8 和图9 所示.(篇幅所限,仅展示初位移分别为4 mm 和10 mm 时的测量结果.)

图7 动态角度验证试验模型Fig.7 Experimental model of dynamic angle verification
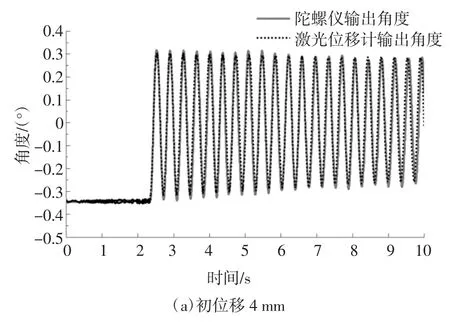

图8 初位移为4 mm 和10 mm 时激光位移计和MEMS 陀螺仪传感器测得的柱的转角响应对比Fig.8 Comparisons of the rotational responses of the column measured by the laser displacement meter and the MEMS gyroscope sensor with initial displacements of 4 mm and 10 mm
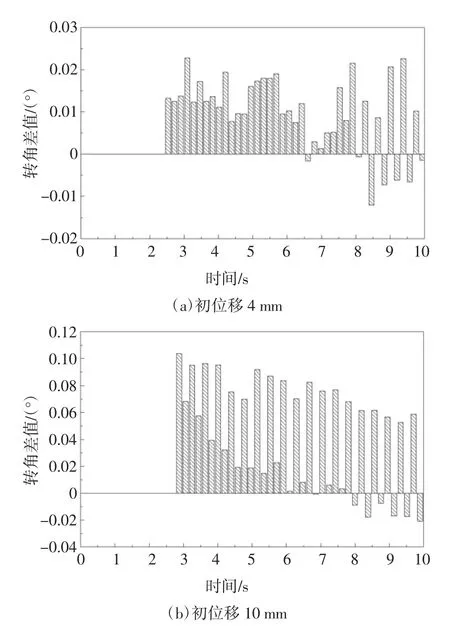
图9 初位移为4 mm 和10 mm 时柱的转角响应在波峰波谷处的相对差值Fig.9 The relative difference of the column's rotational response at the crest and trough of the wave with initial displacements of 4 mm and 10 mm
通过上述图片中MEMS 陀螺仪传感器与激光位移计输出的角度的对比,可以明显观察出:随着初位移的增大,MEMS 陀螺仪传感器与激光位移计输出的角度差值也随之增大.分析误差产生的原因主要为以下两点:1)根据动转角拟合原理,应保证激光位移计发射的激光,门式框架受激励后振动的二维平面,绞盘上绳子施加力的方向均在同一个平面内.由于现场试验条件限制,很容易产生误差.2)激光位移计所测量构件平面的表面不够平整.综合来看,在结构初位移为10 mm 以内,可以基本保证MEMS 陀螺仪传感器进行动态角度测量的精度在0.1°.
5.2 MEMS 陀螺仪传感器的时域识别
5.2.1 试验模型
试验结构模型为如图10 所示的一个3 层2 跨的钢框架结构,框架模型整体尺寸为1 m×1.6 m,首层层高为0.6 m,二、三层层高为0.5 m,框架柱的间距0.5 m,梁、柱均采用50 mm×3 mm 的截面尺寸的钢薄板.梁柱节点处采用尺寸为∟18 mm×18 mm×3 mm 的角钢加M6(螺纹直径6 mm)×16(螺纹长度16 mm)的螺栓连接,如图11 所示.框架模型构件采用Q235 钢,取0.5 m 长的钢梁构件做测试,实测质量密度为7 832.60 kg/m3,用脉冲锤击法识别梁的固有频率,然后利用固有频率识别梁的弹性模量,经过10 次测试平均得到钢梁的弹性模量为2.072×1011N/m2,基于弯剪型结构计算模型,可得钢框架结构的层间抗弯刚度参数EI 的计算值为22.622 1 N/m.

图10 框架试验的结构模型Fig.10 Structural model of frame test
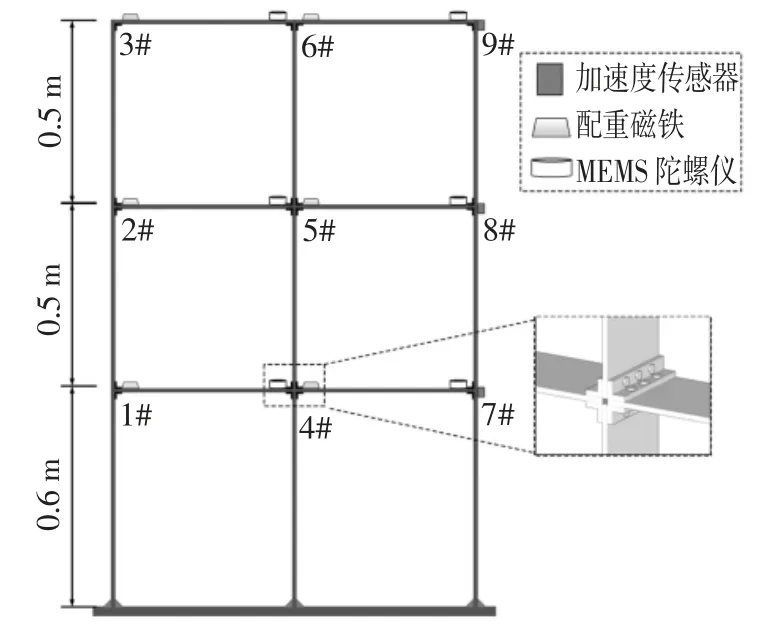
图11 传感器布置示意图及节点详图Fig.11 Details of the joint and sensor deployment
5.2.2 测试方法及结果
用脉冲锤击法对框架结构进行动力测试,由于结构完全对称,可将框架左侧与右侧梁柱连接节点的转动响应视为相等,仅在一侧布置MEMS 陀螺仪传感器.冲击激励使用美国PCB 力锤,加速度信号由PCB 系列压电式加速度传感器333B40 采集,角度及角速度信号由维特智能HWT901B 陀螺仪传感器采集,使用LMS Cadax-8 动态信号分析仪进行试验数据结果的采集.为保证框架结构质量对称,在每根梁上未布置MEMS 陀螺仪传感器的一侧,均放置了100 g 的配重磁铁用于模拟MEMS 陀螺仪传感器的质量.
试验中采用力锤在钢框架的3#节点位置水平从左至右激励一次,力锤的锤击力测量结果经放大后如图12(a)所示,采样频率为100 Hz,采样点数为12 000 个.
传感器测点布置如图11 所示,加速度传感器布置于7#、8#、9#测点,采集得到的加速度响应信号如图12(b)所示.MEMS 陀螺仪传感器布置在4#至9#测点,采集的框架中间4#、5#、6#测点的角度和角速度响应信号分别如图12(c)和图12(d)所示.(篇幅所限,未展示框架右边7#、8#、9#测点的角度和角速度信号).对测试得到的各层加速度响应分别进行傅里叶变换,对相应的各阶频率取平均值得到结构的前三阶模态频率,分别为2.073 Hz、6.704 Hz、11.773 Hz.利用采集得到的结构自由振动时的加速度时程曲线的峰值的对数衰减率求得阻尼比,并根据第1和第2 阶振型的频率,可以得到刚度阻尼系数b,乘以刚度参数EI 可以得到阻尼参数的计算值为0.024 4 N·s/m.
5.2.3 结构参数时域识别
框架模型的梁与柱构件等刚度,可视为一般框架结构.模型中所有梁柱构件具有相同的截面尺寸和材料特性,梁的跨度相等,整体结构对称,基于以下假定对其进行参数识别:1)框架模型的材料为线弹性;2)梁与柱连接节点处采用角钢加螺栓连接,假设梁与柱的连接有足够的刚度,如图13 所示,当框架发生弹性变形时,能保持相交的梁柱杆件之间原有的角度不变[26].3)框架底层用膨胀螺丝固定于地面,在结构分析中忽略框架的平面外变形.4)梁与柱的轴向变形和剪切变形较之转动变形可以忽略,因此假设框架同一层内的各梁柱连接节点的水平位移均相等.
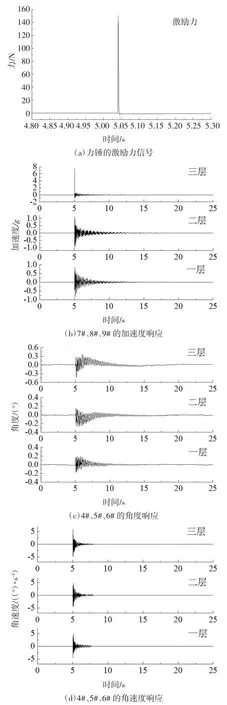
图12 动力测试的响应信号Fig.12 Response signal of dynamic test
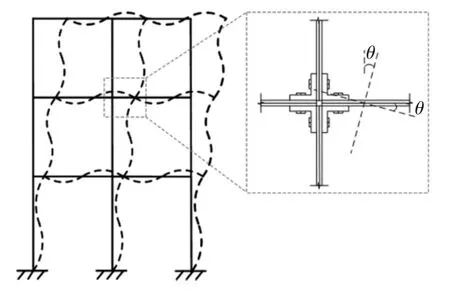
图13 考虑梁柱弯曲变形的框架结构模型Fig.13 Frame structure model considering bending deformation of beams and columns
试验结构模型共18 个自由度,包含9 个平动自由度和9 个转动自由度.基于同一层内节点的水平位移均相等的假设,可将上部结构的平动自由度简化成3 个.考虑转角重构和转角实测两种工况,由于前者将由平动响应重构转动响应,所以将9 个转动自由度简化为3 个,后者则考虑所有的转动自由度.最终两个工况的计算模型如图14 所示.
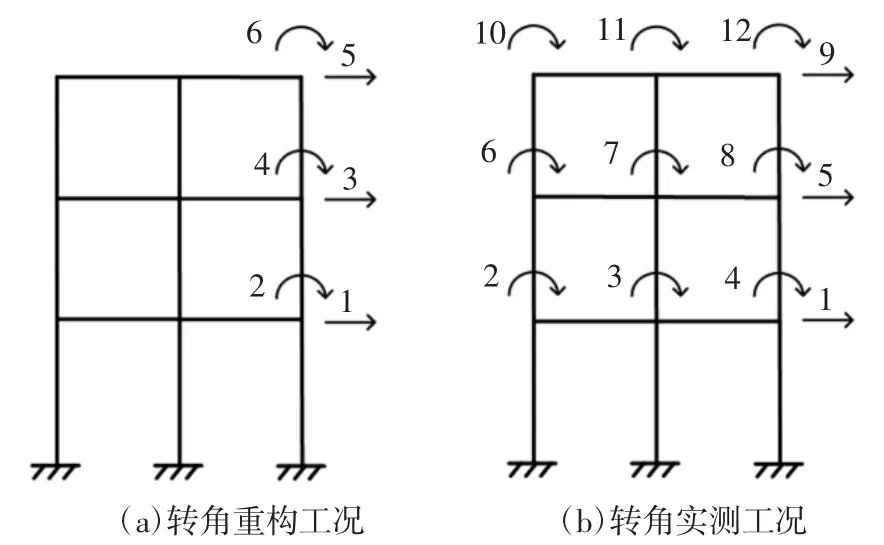
图14 框架试验的结构计算模型Fig.14 Structural calculation model for frame test
已知MEMS 陀螺仪传感器和配重磁铁的质量均为100 g,根据钢梁构件的尺寸和质量密度,可求出梁单元的质量,同理可求出柱单元的质量,进而可求得4×4 阶的单元质量矩阵.将单元质量矩阵组装后可获得框架结构最终协调质量矩阵,转角重构和转角实测工况分别采用6×6 阶和12×12 阶的协调质量矩阵.根据第3 节所述方法,可以构造参数识别的方程式(19),转角重构工况下直接采用3.2 节的公式,转角实测工况下,当识别第1、2 层时,式(19)中:
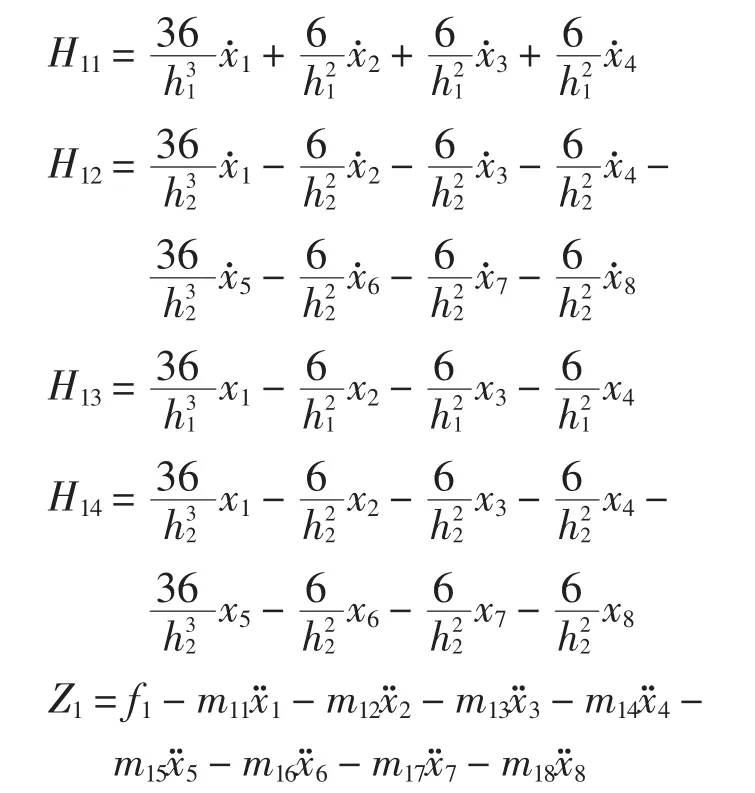
当识别第3 层时:
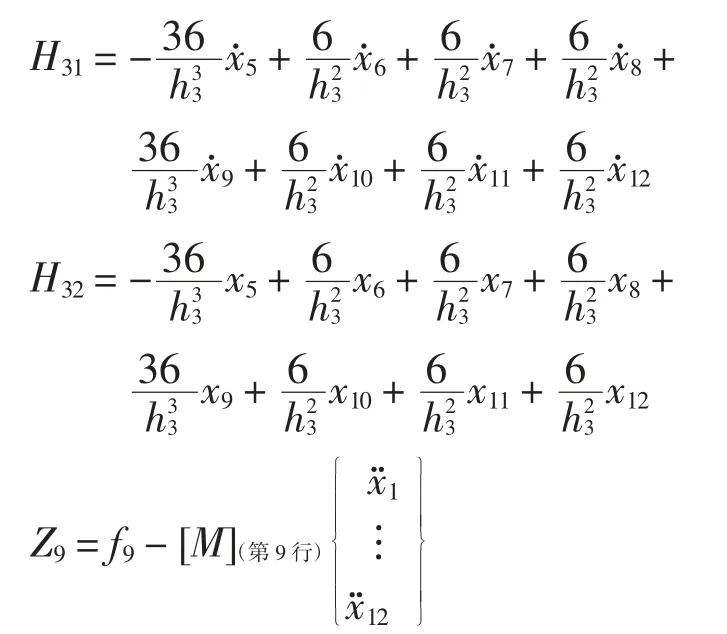
将响应信息、外激励、质量矩阵和层高代入上式,由最小二乘递推算法识别出结构的刚度和阻尼参数如表4 所示,刚度参数与阻尼参数的收敛曲线如图15 所示.
从识别结果可看出,转角实测工况下的刚度参数识别效果明显优于转角重构工况,转角重构工况下的最大和最小误差分别为20.36%和14.38%,转角实测工况下的最大和最小误差分别为13.92%和7.84%.阻尼参数的识别结果受噪声影响较大,失去参考价值.

表4 转角重构与转角实测工况下刚度、阻尼参数的识别结果对比Tab.4 Comparison of identification results of stiffness and damping parameters under angle reconstruction and measured conditions
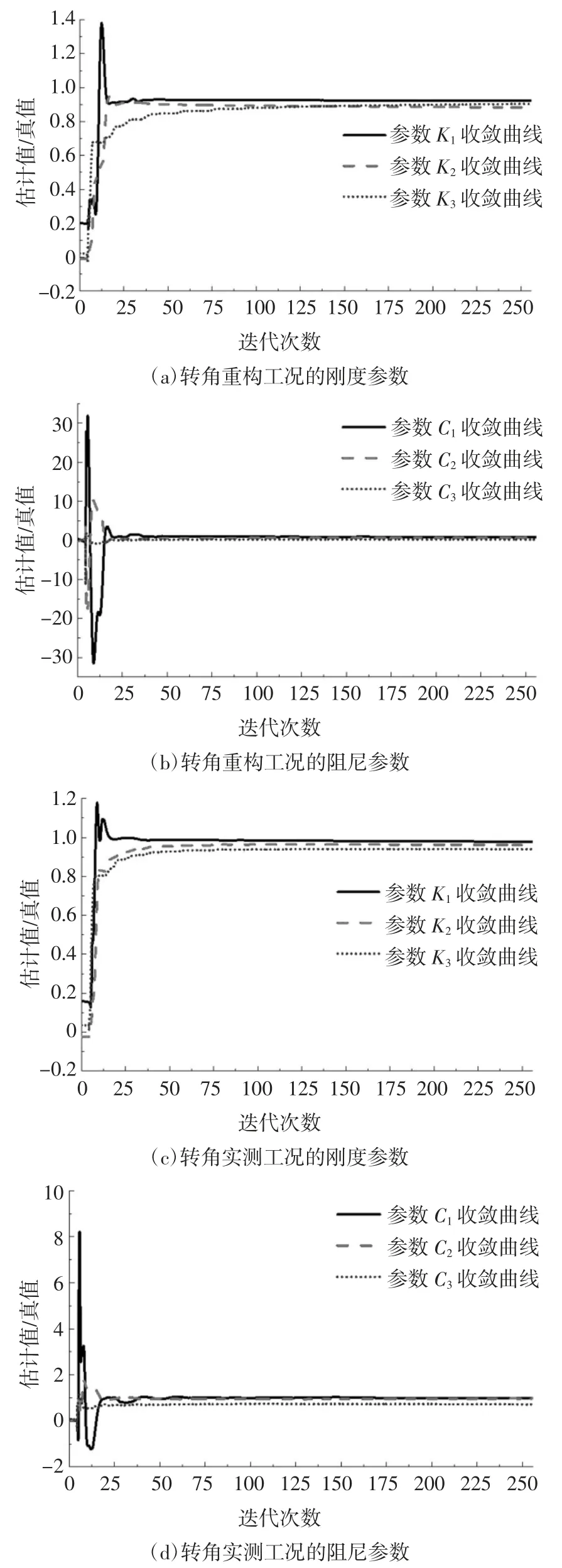
图15 转角重构与转角实测工况下刚度参数与阻尼参数估计收敛过程Fig.15 Parameter estimation convergence of stiffness and damping parameters for angle reconstruction and measured conditions
分析转角实测工况下刚度参数识别的误差产生的原因有以下可能;其一,由加速度响应重构速度、位移响应的过程中,由于存在趋势项和噪声,会使得积分结果产生误差.其二,由于该框架结构的转动变形较小,而MEMS 陀螺仪传感器的动态测量精度仅为0.1°,因此识别效果不够理想.其三,受实验条件限制,由于MEMS 陀螺仪传感器为接触式传感器,不能完全测得节点连接处的实际转动变形,只能以节点附近的转动变形近似替代.但使用MEMS 陀螺仪传感器测量的转角精度仍然高于用广义逆方法重构出的转角,这为转动信息的准确测量提供了新的思路.
6 结论
基于广义逆方法重构转角信息和采用挠曲线拟合的方式重构转角信息,提出采用商业级的MEMS陀螺仪传感器测量角度和角速度响应,改变了传统的仅测试位移类响应的方法,对响应信息进行了直观补充.然后通过最小二乘递推算法识别弯剪型结构的刚度和阻尼参数,得出的结论如下:
1)基于挠曲线拟合方法对MEMS 陀螺仪传感器的角度测量精度校验,主要用来验证动力试验条件下测量的角度是否准确.本文采用的陀螺仪传感器HWT901B 在初位移为10 mm 内可保证动态角度精度为0.1°,试验时,测得钢框架结构的最大位移为4 mm 左右,受到力锤激励后的最大角位移为0.3°左右,其动态角度精度约为0.02°,精度误差约为6.67%,该传感器基本可以满足实验要求.
2)实际工程中的结构形式更复杂,刚度也更大,相应的转动响应的振幅更小,因此对使用的传感器灵敏度要求更高,花费也相对较高.部分位置如节点连接处的转角如何准确测量、如何采用信号处理算法及误差补偿技术提高MEMS 陀螺仪的性能,从而提高其精度仍是值得进一步研究的课题.
3)根据算例分析和试验研究发现,基于广义逆理论重构转动信息的方法需要使用位移、速度、加速度响应分别来重构角位移、角速度、角加速度响应.试验时,通常只测量位移类响应中的加速度响应,加速度响应积分成速度、位移响应的过程中会产生误差.由位移类响应重构转角类响应的过程中,会将在位移类响应中累积的误差带入转角类响应.同时,广义逆方法本身也存在误差.以上原因,导致重构转角下的刚度参数识别效果不如直接测量转角理想.
4)采用MEMS 陀螺仪传感器直接测量转动响应在实测框架中的平均误差为11.13%.相比于由广义逆方法重构转动响应的平均误差17.07%,误差减少了5.94%.说明使用最小二乘递推算法对弯剪型结构进行刚度参数时域识别时,使用转角响应测量值的方法更好,而且与广义逆重构转动响应的方法相比,无需进行复杂计算也不受平动响应的影响.
本文在常规的仅测量平动信息的基础上补充了转动信息的实测数据,使时域识别的结构物理参数更为准确,对结构的健康监测具有一定参考价值.

