MTVMD 对结构减震参数优化及偏离性分析

陈政清，张继峰，牛华伟，朱洋

（湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙 410082）

我国地处环太平洋地震带和欧亚地震带之间，地震基本烈度6 度及6 度以上地区几乎遍布全国，地震造成的桥梁损坏非常严重[1].桥梁抗震方法主要有基础隔震、耗能减震和振动控制[2].李立峰等提出剪力键配合滑板式橡胶支座能起较好减震效果，但需确定合理的剪力键数量[3].李晓波指出大跨度连续梁Lock-up 装置可合理分配主梁地震惯性力，但不耗散地震能量，且改变了结构动力特性[4]；张文学等提出了加速度锁死销装置并通过数值模拟其对连续梁桥具有良好的减震效果，但减震效果取决于锁死球运动轨迹[5]；李勇等以加装了黏滞阻尼器的连续梁桥进行振动台试验，试验表明黏滞阻尼器能减小固定墩墩顶及活动支座的纵向位移[6].

近年来，土木工程领域发展了利用惯质元件产生的惯性力进行结构抗震的新方法，其通过滚珠丝杠、齿轮齿条及杠杆摆等力学放大机制可获得的表观质量远大于实际质量.Watanabe、Nakamura 和陈政清等分别把惯质元件与不同形式的阻尼元件联合形成黏滞质量阻尼器、电磁质量阻尼器和电涡流质量阻尼器，产生的大量级抵抗力达到了结构减震需求[7-9].Ikago 等提出先将惯质元件和黏滞阻尼元件并联，再与弹簧串联，形成调谐黏性质量阻尼器（TVMD），并详细推导了无阻尼单自由度结构在简谐荷载作用下TVMD 最优参数解析式[10].新城季樹等研究了多质点系TVMD 的布置方式及其减震效果，采用数值法和解析法获取阻尼器的最佳参数[11].文永奎等详细阐述了TVMD 用于单自由度时的减振机理，分析了附加刚度和附加阻尼效应，通过基于H2 性能的梯度优化法完成MTVMD 的参数优化[12].阎武通等建立了地震作用下安装了MTVMD 的多自由度结构的状态空间控制模型与传递函数模型，提出了分步参数扫描法进行MTVMD 的参数优化[13].裴星洙等建立了安装TVMD 的钢框架结构在地震作用下的能量方程，提出了质量阻尼和黏性阻尼能量分散系数的简化计算公式，并利用时程分析法验证了其准确性[14].中南滋樹等采用定点理论优化了两重调谐黏性质量阻尼器参数，通过试验验证了两重调谐质量阻尼器减震效果远胜于单重调谐黏性质量阻尼器[15].

以往研究提出的TVMD 参数优化方法多针对单调谐频率黏性质量阻尼器，对多调谐频率黏性质量阻尼器研究甚少，且尚未考虑实际工程中MTVMD系统自身参数的随机偏离，没有对参数偏离后MTVMD 的减震效果做出有效评估.针对以上不足，本文研究了多调谐频率黏性质量阻尼器的减震性能，分析了单自由度结构在简谐激励作用下的动力响应，给出了基于位移及加速度响应为控制目标的MTVMD 参数优化方法，探究了服从正态分布的MTVMD 参数在最不利偏离状态时，结构阻尼比、质量比、调谐频率个数和参数最大偏离率对减震性能的影响，对MTVMD 的设计具有一定的参考价值.

1 MTVMD 减震机理与参数优化方法

MTVMD 附加系由多个子TVMD 并联而成，假定各子TVMD 阻尼均为线性黏滞阻尼，可将被控结构和安装了MTVMD 的系统简化为图1 所示的力学模型，mp、kp和cp分别为主结构的质量、刚度和阻尼系数，固有频率，阻尼比ξp=cp/2mpωp.mi、ki和ci分别为MTVMD 系统中第i 个子TVMD 的质量、弹簧刚度和阻尼系数，固有频率，阻尼比分别为主结构相对基础的位移、速度和加速度，xi为第i 个子TVMD 惯质两端的相对位移.

图1 结构-MTVMD 系统力学模型图Fig.1 Structure-MTVMD system mechanics model

根据结构-MTVMD 系统的力学计算模型可得其运动方程为：

式中：fi为第i 个子TVMD 对主结构的抵抗力，为地震波加速度，改写成矩阵形式为：

当地震波xg为一简谐荷载时，其复数形式为：

式中：δ 为简谐荷载的振幅，ω 为简谐荷载的圆频率，j 为虚数单位.

则式（3）具有相同形式的解如下：

式中：μi=mi/mp，fi=ωi/ωp，h=ω/ωp.

假定各子TVMD 质量mi相等，当k1=k2=…=kn，c1=c2=…=cn时，式（11）（12）为STVMD 控制下的动力放大系数，系统只具有一个调谐频率；当k1≠k2≠… ≠kn，c1≠c2≠… ≠cn时，式（11）（12）为MTVMD 控制下的动力放大系数，系统具有n 个调谐频率.

MTVMD 参数优化，即是找到一组（k1，c1，…，kn，cn），使得目标函数式（11）或式（12）在变量h 定义域内的峰值最小，数学表达式如下：

模式搜索法是一种不需要对目标函数求导的直接优化方法，具有迭代简单，编程容易的特点.对于式（11）（12），不易求得对各参数的偏导数，因此采用模式搜索法具有极大的优势.传统模式搜索法求解含n个变量的函数f（x1x2… xn）最小值的计算流程如图2（a）所示[16].

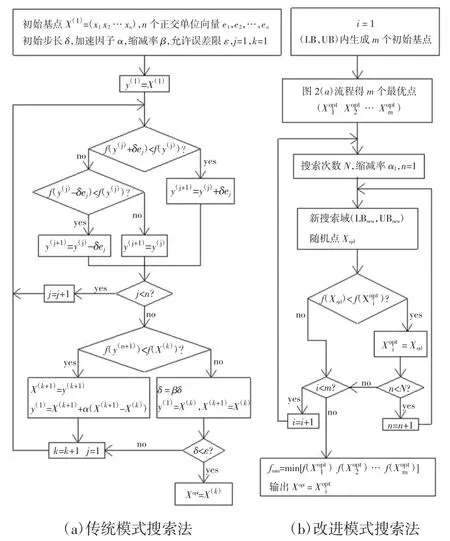
图2 模式搜索法计算流程图Fig.2 Pattern search method calculation flow chart

传统模式搜索法求得的最优解与初始基点和允许误差ε 大小有关，可能陷入局部最优解.为了改善传统模式搜索法的全局寻优能力，在搜索范围（LB，UB）内随机生成m 个初始基点（），其中第i个初始基点的计算如式（15），式中LB 和UB 分别为搜索上、下边界，rand（0，1）为0 到1 之间的随机数，利用传统模式搜索法求得与各个初始基点相对应的最优解（）.

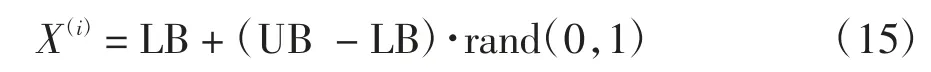
为了提高该算法的局部寻优能力，首先根据式（16）生成各最优解的邻域（LBnew，UBnew），式中α1为搜索范围收缩率，再根据式（17）在邻域内随机生成初值Xsjd，对已得到的m 个最优点进行N 次局部寻优，计算流程如图2（b）所示[17]：

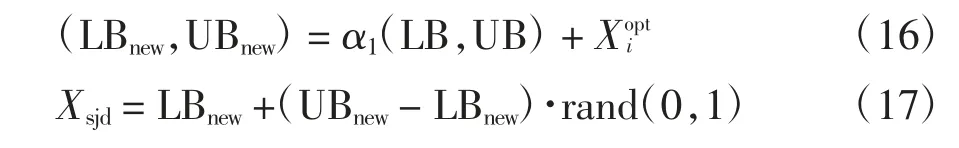
2 MTVMD 参数优化后系统动力响应

2.1 调谐频率个数效应

为研究调谐频率个数对系统响应的影响，取主结构阻尼比ξp=2%，MTVMD 总质量比μ=1%，分别以式（11）和式（12）为目标函数，按改进模式搜索法求得不同调谐频率个数下位移和加速度最优频响曲线，及其对应的最优参数组合分别如图3 和图4 所示.

由图3（a）和图4（a）可知，具有n 个调谐频率的MTVMD 系统，其最优频响曲线有n+1 个等高波峰；调谐频率个数相同时，加速度频响曲线峰值略大于位移，但不超过1%；随着调谐频率个数增多，位移和加速度放大系数峰值都降低，当调谐频率个数大于5 时，峰值降低速率减缓.主结构未加装TVMD 时，其位移和加速度动力放大系数峰值分别为25.00 和25.02，加装STVMD 的减震效果分别为62.47%和62.29%，与文献[12]利用稳态谐振扫频分析所得结果几乎一致，MTVMD 的减震效果更加明显.由图3（b）和4（b）可知，STVMD 的最优调谐频率大于主结构的基频，位移响应最优时的调谐频率略高于加速度，随着调谐频率个数增加，MTVMD 控制的频带宽增大，更有利于结构减震；各子TVMD 的最优频率比近似线性分布；由图3（c）和图4（c）易知，各子TVMD 的最优阻尼比近乎相等，与调谐频率个数呈负相关.考虑位移和加速度得到的最优参数不同，但差距不大，特别是在质量比较小时.工程中如要同时考虑两者，最优参数可取为两者的平均值，也可根据侧重点的不同，可赋予位移和加速度权重后求加权作为目标函数寻找最优解.

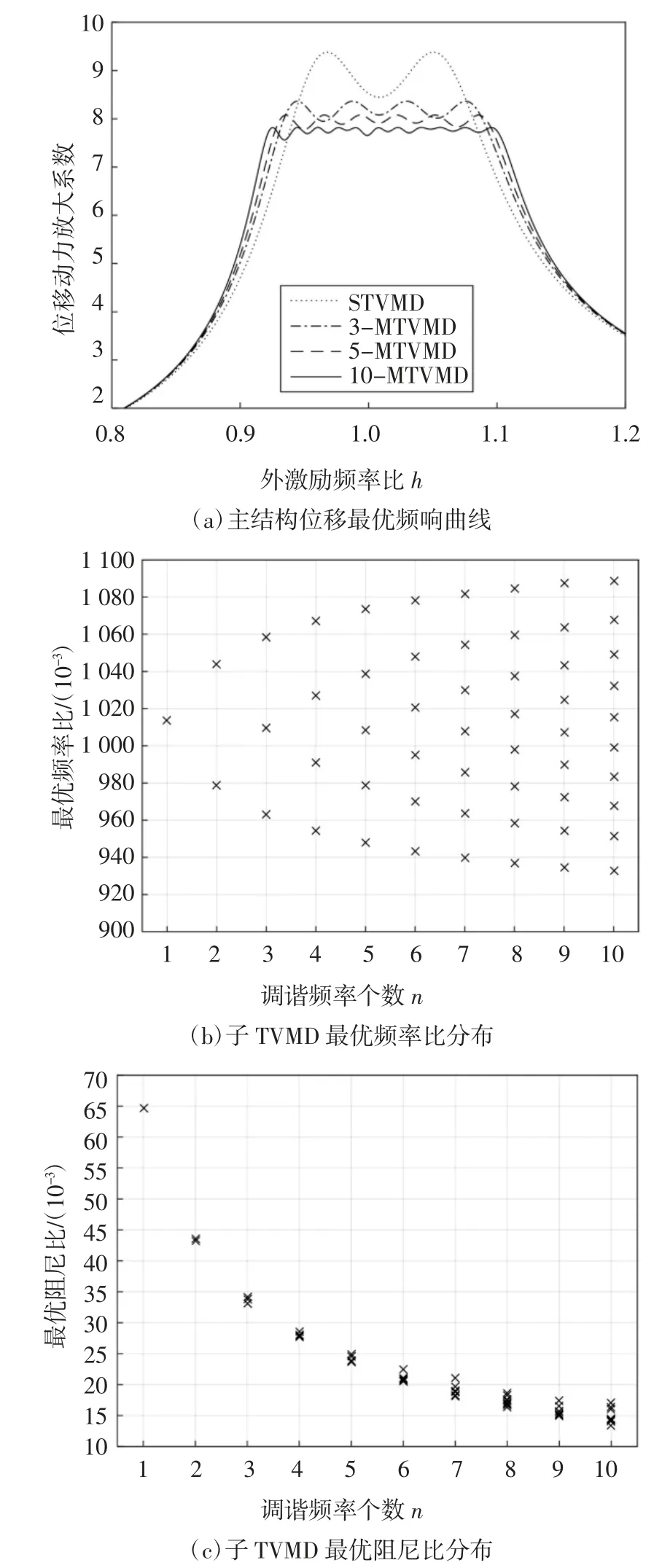
图3 位移动力放大系数最优频响曲线及最优参数分布（ξp=2%，μ=1%）Fig.3 Optimal frequency response curve and optimal parameter distribution of displacement dynamic amplification factor（ξp=2%，μ=1%）

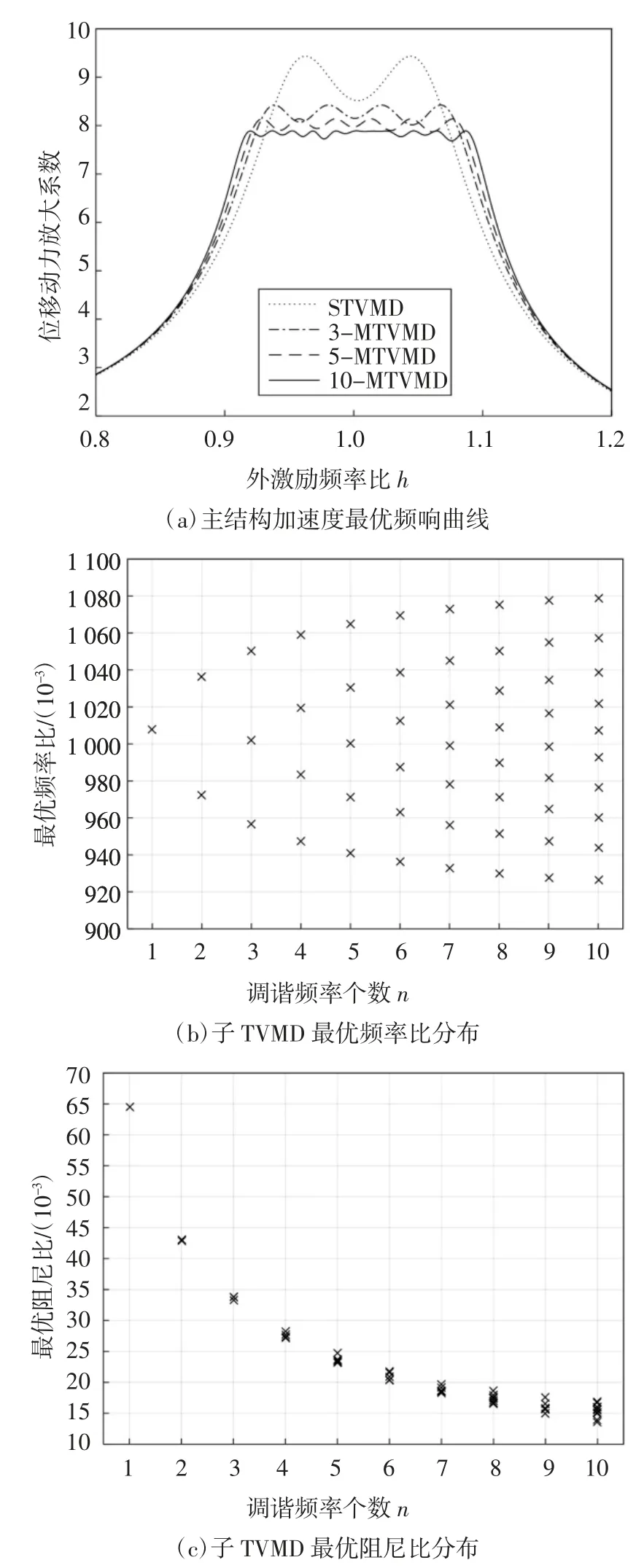
图4 加速度动力放大系数最优频响曲线及最优参数分布（ξp=2%，μ=1%）Fig.4 Optimal frequency response curve and optimal parameter distribution of acceleration dynamic amplification factor（ξp=2%，μ=1%）

2.2 主结构参数变化后的鲁棒性

使用MTVMD 进行减震控制时，主结构参数变化必然导致MTVMD 的频率比和阻尼比偏离最优值，减震效果减弱.主结构的质量通常不会发生改变，仅考虑刚度和阻尼系数的变化.定义评估系统鲁棒性指标为，即主结构参数偏离后动力放大系数曲线峰值，R 越大，表示结构参数变化后减震能力越弱，系统鲁棒性越差.图5～图7 分别是主结构质量、刚度和阻尼系数发生偏离，位移放大系数最优时系统的鲁棒性指标.由图5 及图6 可知，结构质量或刚度发生偏离时，鲁棒性指标曲线呈“V”型，子TVMD 个数相同时，质量比增大，鲁棒性增强；质量比相同，刚度负向偏离时，MTVMD 的放大系数峰值变化幅度大于STVMD，但其鲁棒性仍然优于STVMD，且子TVMD 个数越多，鲁棒性越好.由图7 可知，系统阻尼系数偏离时，鲁棒性指标曲线呈单边下降，结构阻尼系数增大，鲁棒性增强；阻尼系数偏离对MTVMD 带来的影响远不及质量和刚度偏离.结构-TVMD 系统耗能来自结构阻尼和TVMD 提供的阻尼；质量和刚度的变化都会改变结构自身频率，导致按原结构计算得到的TVMD 最优频率比和阻尼比不再最优，使阻尼器的减震作用减弱，系统耗能取决于TVMD，所以鲁棒性指标曲线呈“V”型；而结构阻尼系数变化对结构的频率影响甚微，但对振幅有较大影响.结构阻尼系数变化，程序寻得的TVMD 最优参数变化甚微，减震作用削弱小，结构耗能取决于自身阻尼，阻尼系数增大，耗能增加，鲁棒性增强，所以鲁棒性指标单边下降.

图5 结构在mp 偏离时的鲁棒性Fig.5 Robustness of structure when mp deviates

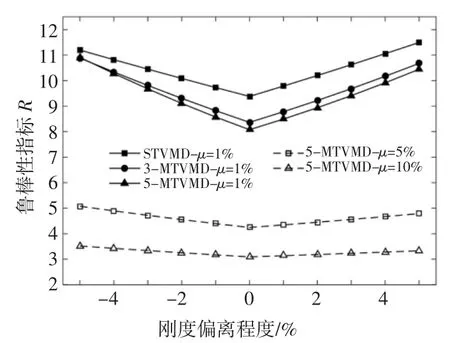
图6 结构在kp 偏离时的鲁棒性Fig.6 Robustness of structure when kp deviates

图7 结构在cp 偏离时的鲁棒性Fig.7 Robustness of structure when cp deviates

3 MTVMD 自身参数偏离可靠性分析

3.1 MTVMD 系统自身参数偏离模型

MTVMD 在实际制作、运输、安装以及使用过程中参数均可能偏离最优值，假定各参数独立且服从正态分布，数学表达式如下：

记子TVMD 频率比和阻尼比的最大偏离率分别为ηf和ηξ，由概率论“3σ”法则可知，一个服从正态分布N（E，σ2）的数落在区间（E-3σ，E+3σ）内的概率为99.74%，几乎为必然事件，则第i 个子TVMD频率比和阻尼比的标准差σfi、σξi可由下式计算：

3.2 MTVMD 减震有效性和可靠性分析方法

为了分析各子TVMD 的频率比和阻尼比偏离最优值引起减震性能的改变，采用蒙特卡罗试验，对参数服从式（20）和式（21）分布的概率模型进行减震有效性和可靠性计算.定义MTVMD 系统减震有效性指标，即MTVMD 参数偏离最优值后动力放大系数曲线峰值.当MTVMD 参数发生随机波动时，通过N 次蒙特卡罗试验得N 个r 值并按降序排列，取前10%的平均值rmax来评估最不利偏离状态时的减震有效性，其表达式见式（24）.rmax越大，MTVMD 减震有效性越弱.

定义MTVMD 系统最不利偏离状态时的减震可靠性指标βmax如式（23），即参数偏离后与参数最优时减震有效性的波动程度.βmax越大，MTVMD 减震可靠性越弱.

式中：ropt为阻尼器处于理想工作状态时，即参数最优时的减震有效性.

3.3 数值模拟结果与分析

取子TVMD 频率比和阻尼比的最大偏离率ηf和ηξ分别为5%和25%，蒙特卡罗试验次数N=10 000，以位移放大系数曲线为目标函数，分别对STVMD 和MTVMD 系统进行分析.工程中考虑工作空间不足或避免因单个阻尼器质量过大而引起局部应力过大，会采用分布布置形式，将STVMD 分为参数均相同的n 个子TVMD，此时仍只具有单一调谐频率；MTVMD 各子TVMD 参数各不相同，具有n 个调谐频率.图8 和图10 是计算了5 种工况下STVMD 和MTVMD 两种系统在最不利偏离状态时的减震有效性指标，图9 和图11 为减震可靠性指标.

图8 不同结构阻尼比的有效性指标rmax（μ=5%）Fig.8 The validity index rmax of different structural damping ratio（μ=5%）

图8 和图10 表明在最不利偏离状态时，随着子TVMD 个数的增加，STVMD 的减震有效性越来越强，增强趋势先快后慢，减震有效性指标是反比状曲线，呈收敛状，可预测最终将趋于参数最优时的减震有效性；然而，MTVMD 的减震有效性是先增大后减小，减震有效性指标是凹形曲线，呈发散状，凹点对应的子TVMD 个数即为最佳调谐频率个数.一方面MTVMD 的减震有效性随着子TVMD 个数的增加而增强，另一方面，MTVMD 的子TVMD 参数互不相同，其参数组合复杂性随子TVMD 个数增加而增大，因此给予参数微小扰动便会引起减震有效性减弱.所以当子TVMD 个数较少时，前者为主导因素，子TVMD 个数达到一定量时，后者为主导因素，因而MTVMD 减震有效性指标成凹形曲线，存在最优调谐频率个数.

图9 不同结构阻尼比的可靠性指标βmax（μ=5%）Fig.9 The reliability index βmax of different structural damping ratio（μ=5%）

图10 不同质量比的有效性指标rmax（ξp=2%）Fig.10 The validity index rmax of different mass ratio（ξp=2%）

另外，随着主结构阻尼比和阻尼器质量比增大，STVMD 和MTVMD 系统的减震有效性均增强.数值结果表明，在自身参数偏离模型的最不利状态时，STVMD 的减震有效性会优于MTVMD，子TVMD 个数越多、结构阻尼比或质量比越小时表现越明显，图10 中，ξp=2%，μ=1%时，STVMD 的减震有效性始终优于MTVMD.

图9 和图11 表明，在自身参数偏离的最不利状况下，STVMD 的减震可靠性随着子TVMD 个数的增加而增强，MTVMD 则相反；STVMD 的减震可靠性明显优于MTVMD，子TVMD 个数越多，优势越明显.增大结构阻尼比和质量比均能提高STVMD 和MTVMD 的减震可靠性.减震可靠性是减震有效性的另一表现形式，所以变化规律与减震有效性相同.

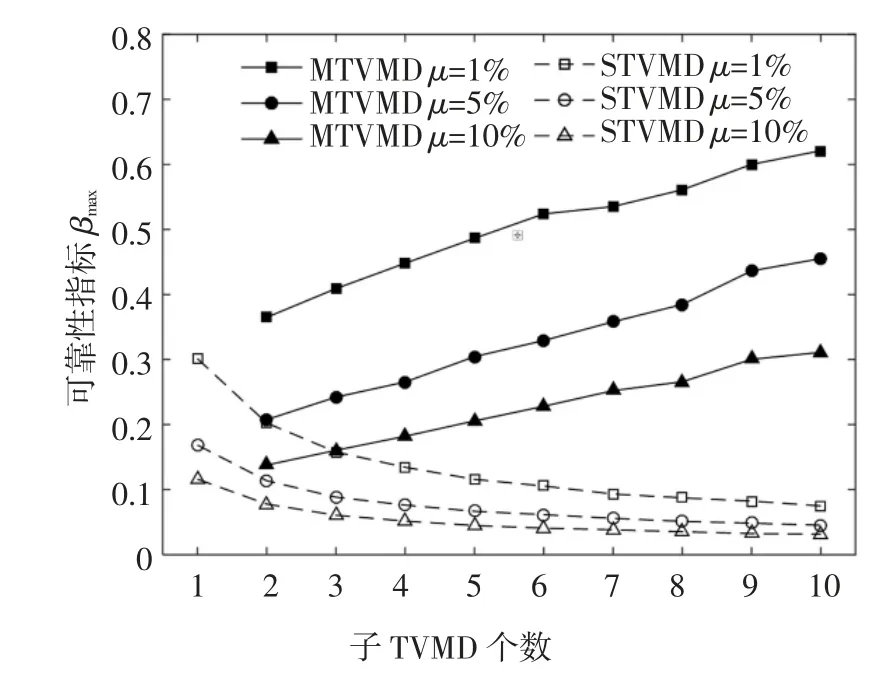
图11 不同质量比的可靠性指标βmax（ξp=2%）Fig.11 The reliability index βmax of different mass ratio（ξp=2%）

为了分析MTVMD 自身参数偏离模型的最大偏离率对减震性能的影响，取最大偏离率η=ηf=ηξ∈（0，0.6），间隔0.02 计算一次，STVMD 和MTVMD 的子TVMD 个数均为5，ξp=2%，蒙特卡罗数N=10 000进行数值计算.图12 与图13 描述了最不利偏离状态时，STVMD 和MTVMD 两种系统的减震有效性与可靠性.

由图12 和图13 可知，在各种质量比下，最大偏离率较小时，MTVMD 减震有效性和可靠性优于STVMD，随着最大偏离的增大，STVMD 和MTVMD的减震有效性和可靠性指标逐渐增大，呈发散状态，STVMD 减震性能优于MTVMD，说明MTVMD 自身参数发生较小波动时，各参数可能彼此靠近最优值；由图13 可知，当最大偏离率大于0.3 时，STVMD 和MTVMD 的减震可靠性下降速度加快，但质量比较小时（μ=1%）并不相符，原因在于小质量比MTVMD 系统自身参数发生较大偏离时，减震效果已经趋于无控结构，也说明了较大质量比的MTVMD 系统更能抵抗因自身参数偏离导致的减震性能变差.

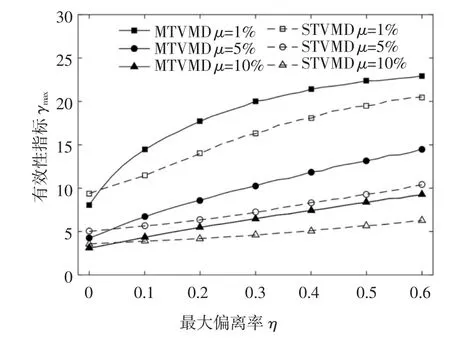
图12 不同最大偏离率的有效性指标rmax（ξp=2%）Fig.12 The validity index rmax of different maximum deviation ratio（ξp=2%）

图13 不同最大偏离率的可靠性指标βmax（ξp=2%）Fig.13 The reliability index βmax of different maximum deviation ratio（ξp=2%）

4 结论

1）改进模式搜索法能较准确搜寻以位移或加速度响应为控制目标时的MTVMD 最优参数；系统参数最优时，MTVMD 的减震效果优于STVMD，调谐频率个数越多，减震效果越好.

2）主结构参数偏离会影响MTVMD 的减震性能，提高结构阻尼比和MTVMD 的质量比及子TVMD 个数，能够提高MTVMD 的减震性能，同时可以提高系统鲁棒性.

3）结构及MTVMD 系统参数不变或只有结构自身参数发生变化时，增加子TVMD 个数可增强减震性能和鲁棒性；MTVMD 自身参数发生偏离时，STVMD 的减震有效性和可靠性随着子TVMD 个数增加而增强；MTVMD 则存在一个最优子TVMD 个数使得减震有效性最佳；MTVMD 减震性能与参数最大偏离率呈负相关.

4）实际工程中，黏滞阻尼器多为油阻尼器，漏油现象严重，必然导致阻尼器自身参数发生变化而偏离理论工作状态，从而削弱了阻尼器的减震作用.所以，在设计MTVMD 时，当不能保证阻尼器性能稳定、质量绝对可靠时，不要盲目追求增加子TVMD 个数来增强鲁棒性.