锁脚锚管-钢拱架在软岩隧道中的力学稳定性研究

梁辉如，王永东，燕 新，刘俊锋, 彭 浩，郭旭东

(1．广东省路桥建设发展有限公司,广州 510507;2.长安大学 公路学院,西安 710064)

软弱围岩隧道的施工技术一直是隧道建设中的难点，软弱围岩隧道开挖后变形量大，变形速率快且持续时间长，有显著的软化、蠕变特性，容易造成了严重的隧道变形和支护结构失效等问题[1-3]，针对隧道现场出现的大变形问题，很多学者提出不同的控制措施[4-7]，保证了围岩的稳定性.

岩石作为一种特殊材料，结构复杂，内部受力不均匀，破坏模式不一，为了进一步研究岩石的力学破损行为，学者们提出了三种蠕变理论，即应变硬化理论[8]、疲劳理论[9]和裂隙扩展理论[10].在此基础上,Attewell[11]论述了支护结构与围岩应力、应变之间的关系，指出隧道围岩应力随支护结构刚度的增加而增大，而应变则随支护结构刚度的增加而减小，因此支护结构形式对围岩稳定性起着关键性的作用.随着支护形式的发展，锁脚锚杆-钢拱架支护理念在软弱围岩支护中的地位不断凸显，其已经逐渐取代了系统锚杆[12].锁脚锚杆(锚管)作为初期支护的重要措施之一，不仅可以提高围岩的整体性，还可以保证钢拱架的支护效果.Czarnecki等[13]根据锚杆试验，提出了剪切与张力、边缘距离、间距、开裂等之间存在相互作用，给出了锚杆的极限强度的平均值.杨双锁等[14]运用理论分析及数值计算的方法，总结出锚杆的力学本质，即提高锚固体的内聚力、弹性模量、减小锚固体的泊松比以及改善锚固体所处的应力状态.刘泉声等[15]给出了锚杆锚固的基本原理，即依靠岩体自身的抗剪力作为荷载传递的主要方式，并发挥岩体的自稳能力来保持地层开挖面的稳定.陈丽俊等[16]在分析了锁脚锚杆的受力特性后，得出以下结论:锁脚锚杆最不利受力位置位于与钢拱架焊接的部位，该部位应焊接牢固，并且在计算模型中宜考虑焊接部位的弯矩传递；锁脚锚杆横向效应主要集中在端部附近区域，该区域围岩应重点加固，且锚杆过长对发挥其横向作用并无贡献.

为了解锚管-钢拱架对围岩的作用机理，国内外学者一直进行着不同的本构模型研究.Bernaud等[17]从锚固岩体中提出了一种基于均匀介质化技术的数值计算的方法.朱训国等[18-19]基于Mohr-Coulomb、Hoek-Borwn、Duncan-Chang理论以及锚杆、注浆和岩体耦合理论，给出了锚固的解析本构方程.陈丽俊等[20-21]给出了不同锁脚锚管的计算模型.在锁脚锚管力学研究的同时，曾仲毅等[22]得出了围岩的含水率和膨胀力值是造成隧道支护结构不良影响的关键.张晟斌等[23]通过理论分析，得出随着围岩膨胀率的增大，松动围岩压力也逐渐增大，即膨胀土隧道松动压力计算公式中的修正系数的大小与围岩膨胀率成正比.在以上的研究中，锁脚锚管稳定性的理论公式分析都较为复杂，同时未考虑软岩湿化和膨胀性对锚管-钢拱架的力学影响.

本文作者基于锁脚锚管和钢拱架的力学特征，考虑软岩湿化和膨胀对锚管力学的影响，提出锁脚锚管和钢拱架连接处的破坏判断条件，为隧道设计、施工提供有效的判断依据.

1 锁脚锚管-钢拱架力学模型

首先建立锁脚锚管-钢拱架力学模型，如图1所示.对锁脚锚管和钢拱架连接A点进行受力分析.其中,钢拱架在连接处的弯矩为M1，竖向力为Y1和法向力为X1，锚管端部在连接处的弯矩为M0，剪力为Y0和轴向力为X0，锁脚锚管与水平夹角为β.

2 锁脚锚管力学分析

若要发挥锁脚的作用，不仅要保证锚管不发生轴向滑移，也要保证钢拱架与锚管连接处的稳定性.锁脚锚管稳定性主要从两个方面进行分析：①锚杆轴向滑移稳定性；②锁脚锚管连接处稳定性.

根据锚管与围岩的耦合作用，锚管与围岩耦合模型可分两种[24]：①全灌浆型锚管模型；②摩擦型锚管模型.

2.1 全灌浆型锚管剪应力分布

全灌浆型锚杆剪应力函数分布如图2所示，其中:x0，x1，x2为锚管剪力突变的分界点坐标.

1)在锚管0≤x≤x0段，锚段的锚管不受剪应力作用，其锚管界面上剪应力τb(x)为零，轴管与围岩界面完全开裂，导致此向正应力σb(x)恒定，大小为σ0，表达式如下

τb(x)=0

(1)

σb(x)=σ0

(2)

2)在锚管x0≤x≤x1段，锚管与围岩界面部分开裂，剪应力保持不变，大小为sr.其锚管界面的剪应力和轴向正应力表达式

τb(x)=sr

(3)

(4)

式中：db为锚管直径.

3)在锚管x1≤x≤x2段，锚管与围岩界面部分开裂，剪应力呈线性增长，其锚管界面的剪应力和轴向正应力表达式

(5)

(6)

4)在锚管x2≤x段，其锚管与注浆体界面完全耦合，锚管界面的剪应力和轴向正应力表达式为

(7)

(8)

(9)

(10)

式中：Er、νr、Gr分别为岩体的弹性模量、泊松比、刚度;Eg、νg、Gg分别为注浆材料的弹性模量、泊松比、刚度;dg为钻孔直径，d0为注浆的半径.

根据应力变化连续性，当x=x2时，可得

(11)

式中：P0为锚管的拉拔力.

全灌浆性锚管的拉拔力P0max为

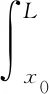
(12)

式中：L为锚管长度.

2.2 全摩擦型锚管型

对于摩擦型锚管，当截面发生开裂后，界面剪切强度和峰值剪切强度几乎相等，剪应力函数分布如图3所示，即sr=sp=s，s为注浆岩体与锚管完全耦合时，锚管界面剪应力的大小.

1)当0≤x≤x2时，截面剪切强度达到岩体的剪切强度，此时岩体发生部分开裂，其剪应力和轴向正应力表达式

τb(x)=sr

(13)

(14)

式中：A0为锚管的横截面积.

2)当x2≤x时,注浆岩体与锚管完全耦合，其剪应力和轴向正应力表达式

(15)

(16)

根据应力变化的连续性，当x=x2时，可得

(17)

全摩擦型锚管的拉拔力为

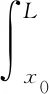
(18)

根据以上分析，可知全灌浆型锚管和摩擦型锚管最大的拉拔力与锚管长度有关，但锚管过长对锚管的抗剪性没有明显的增加作用，与文献[11]结论一致，因此锚管的长度设置不仅要考虑其加固效果，更要注重经济效应.

3 钢拱架力学模型

为了保证锁脚锚管沿着轴向不发生大变形，首先假设轴向位移为零.以隧道中线对称进行切开，采用结构荷载法对其进行分析，如图4所示.

考虑软岩遇水软化和膨胀的效应的影响，引入修正系数η(围岩软化、膨胀前后松动压力的比值)[16]，围岩压力为

(19)

e1=ηγK

(20)

e2=ηγ(H+f)K

(21)

式中：K为侧压力系数;f为上台阶或下台阶开挖高度，即钢拱架的高度;γ为岩体的重度;ε为岩石坚固性系数;a1为氏压力拱半跨宽度;H为隧道埋深;l为上台阶或下台阶的跨度.

钢拱架不仅要承受围岩施加的主动荷载，还要承受着围岩产生的弹性抗力，在两者的作用下，发生侧向变形.为了求解钢拱架与锚管之间的作用力，首先分别求出主动荷载和弹性抗力对钢拱架拱顶的弯矩M2和X2水平力，钢拱架在拱顶出处的弯矩和水平力为

M2=M2p+M2σ

(22)

X2=X2p+X2σ

(23)

式中：M2p、X2p分别为拱顶在主动荷载下求得的弯矩和水平力；M2σ、X2σ分别为在弹性抗力下求解的弯矩和水平力.

3.1 主动荷载

根据拱顶的位移连续条件和边界条件，可求得钢拱架在主动荷载下的弯矩M2p和水平力X2p为

(24)

(25)

3.2 弹性抗力

在弹性抗力的作用下，求解过程与主动荷载求解的过程一致，弯矩和水平力大小为

(26)

(27)

式中：σh为最大抗力系数;aik(i,k=1,2)为钢拱架拱顶处的单位位移，ai0为钢拱架拱顶处的荷载位移，具体系数计算见文献[18].

将(24)～(27)式带入(22)～(23)式可求得钢拱架拱顶处的弯矩M2和水平力X2.

4 锚管连接处受力分析

锚管一端打入岩体，一端留在岩体之外，并与钢拱架进行焊接相连，限制钢拱架的变形与下沉.锚管与钢拱架的焊接处距离围岩表面一般为l0=5～10 cm；针对围岩大变形处，预留变形为l0=12～20 cm左右；在某些超挖地方，超挖距离为l0=50 cm左右，因此对锚管端部的抗弯稳定性需要进一步分析.

将锚固于岩体中的锚管假设为悬臂梁，锚管与围岩交于m截面，m截面不会发生竖向移动，如图5所示.

根据材料力学知识[25]可知，与围岩接触面的弯矩最大值弯矩在m截面，最大值为

Mm=M0+l0Y0

(28)

式中：l0为钢拱架与锚管的连接点到m截面的距离;M0为锚管端部承受的弯矩;Y0为锚管端部的法向应力.

4.1 端部接触力分析

根据钢拱架顶部的边界条件，即转角与水平位移为零，根据结构力学方法可求得连接处的水平力X1、弯矩M1和竖向力H1为

(29)

锚管端部的轴力X0、弯矩M0、剪力Y0大小为

(30)

4.2 锚管稳定性条件

锁脚锚管若要充分发挥其锁脚作用，锚固段不能发生轴向滑移破坏，悬臂端不能发生弯曲破坏.根据材料力学可以给出判断条件表达式

P0max≥X0

(31)

σmax≤[σ]

(32)

式中：σmax为工作截面最大正应力;[σ]为锚管允许最大的弯曲正应力.

外露出岩体的锚管强度计算表达式

(33)

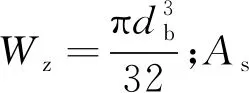
当σmax≤[σ]时，则m截面稳定.

若m截面稳定，则外露锚管的任何截面都保持稳定.

5 试验验证

以梅州东环高速线其古顶隧道为例进行验证，取隧道设计速度为80 km/h，双向四车道.围岩主要由二叠系中统龙潭组全～强风化砂岩、上统文笔山组强风化～微风化炭质泥岩、砂岩等组成，局部侵入有花岗岩岩脉，岩体破碎，强度较低，围岩级别为Ⅳ～Ⅴ级.

隧道穿越此类泥岩地层时，变形量大，变形速度快、持续时间长、受开挖扰动大，后期具有蠕变特性而无明显减缓趋势的特点.岩体在遇水后，会产生软化和膨胀的现象，改变了支护结构的受力特点，因此可能会出现喷射混凝土开裂、钢架扭曲、断裂和净空侵限等施工问题，导致施工进度极其缓慢，如图6所示.

选取其古顶隧道中强风化炭质泥岩段进行计算.本段隧道采用三台阶开挖法，以人工或机械开挖为主，可配合少量的松动炸药进行掘进.隧道埋置深度36 m，锁脚锚管直径φ为42 mm，厚度为5 mm，长度为3.5 m，打入角度为15°，强度为205 Gpa，工字钢采用的型号为I20a，纵向间距60 cm，由于炭质泥岩破碎，局部最大超挖量为50 cm，其中预留变形量12 cm.上台阶宽度为12.6 m，上台阶至拱顶高度为3.2 m，软化和膨胀修正系数η取值1.3，侧压力系数K取值0.33，如图7所示.

5.1 数值计算

为了避免中、下台阶施工后对上台阶锁脚锚杆-钢拱架连接处的影响，仅仅计算上台阶开挖后锚管-钢拱架作用力大小.其中最大抗力系数取值为104.25，钢拱架截面弯矩M2=526.5 kN·m，水平力X2=205.6 kN.根据式(29)，可求得锚管与钢拱架连接处的弯矩M1=473.5 kN·m，水平力X1=318.3 kN，竖向力Y1=389.2 kN.可得锚管m截面处的弯矩Mm=755.66 kN·m，以及锚管轴向力X0=408.19 kN，剪力Y0= 458.32 kN.

5.2 数值模拟计算

采用ANSYS数值软件建立其古顶隧道模型并进行分析.由于隧道长度远大于隧道宽度，可将三维模型简化为二维平面模型，模型长×宽为200 m×140 m，二维模型如图8所示.围岩参数如下：密度为2 000 kg/m，内摩擦角为20°，黏聚力8×104Pa，体积模量18.5 MPa，剪切模量21.7 MPa.

钢拱架采用梁单元Beam模拟，锚杆采用Cable单元模拟，其中钢拱架折算混凝土模量的表达式为

(34)

式中：E0为等效弹性模量；Es为混凝土的弹性模量；Ec为钢拱架的弹性模量；A为总面积,Ac为钢拱架的横截面积.

计算参数如下：混凝土的弹性模量为205 Gpa；钢拱架的弹性模量为2.8×104MPa，总面积为35.578 cm2，钢拱架的横截面积为2.8 m2.

数值模拟流程如下：建立模型—划分网格—设置边界条件—开挖—求解.边界条件设置如下:当x=-100时，x方向位移为0；x=100时，x方向位移为0；当y=-100时，y方向位移为0.

为了避免中下台阶开挖后对上台阶锚管-钢拱架力学的影响，对上台阶开挖过程进行数值模拟.在模拟开挖支护稳定后，可以得出钢拱架的弯矩图、Y和X方向的应力云图，如图9～图11所示.

根据二维模型网格的划分，锚管与钢拱架连接节点为node11和node1，隧道为对称结构，两点取值大小一样，节点的弯矩M1为471.3 kN·m，Y1值为399.6 kN，X1值为325.2 kN.根据式(28)和式(30)，可得锚管m截面处的弯矩Mm、锚管轴向力X0以及剪力Y0.

通过对模拟数值和理论公式计算的数值对比，可知两者锚管端部的弯矩、轴向力和剪力大小基本一致，同时根据锚管的轴力云图可以看出锚管在端部的轴力大小与计算值基本一致，表明了理论公式的合理性.

5.3 稳定性判断计算

根据稳定性判断条件可知，锁脚锚管-钢拱架要保持稳定须满足式(32)和式(33).从图12和图13中可以看出锁脚锚管与地层之间剪应力分布形态和大小.

对数值模拟中各个区段的剪应力进行累加求和，可以得出锚管剪力大小

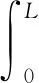
(35)

式中：τi为dx段内剪应力的大小.

根据式(35)求解，可得P0max=421.27 kN，剪力P0max与轴向力X0满足如下关系：P0max≥X0，此时锚管不会产生轴向滑移.

将X0、Mm带入(33)式，可得到σmax值为114.89 GPa.根据强度稳定性判断，σmax≤[σ]=205 GPa，则锚管不会发生弯曲破坏.

根据稳定性条件进行验算，表明锚管-钢拱架满足其稳定性条件.

6 结论

1)基于其古顶隧道现场出现的问题，引入软岩遇水软化和膨胀的效应修正系数η来分析钢拱架的受力性，建立锁脚锚管-钢拱架力学模型，考虑了开挖岩体后产生的松散压力(主动荷载)和支护后产生的弹性抗力影响，给出了锁脚锚管-钢拱架的稳定性判定条件.

2)将稳定性判断依据应用于梅州其古顶隧道工程进行理论计算和模拟验证.根据理论计算，可得锚管与钢拱架连接处的弯矩M1=473.5 kN·m，水平力X1=318.3 kN，竖向力Y1=389.2 kN；根据数值模拟的结果可知，锚管与钢拱架连接点的弯矩M1为471.3 kN·m，Y1值为399.6 kN，X1值为325.2 kN.通过数值模拟验证，可知锁脚锚管-钢拱架稳定性判定条件理论的正确性.

3)通过对数值模拟得出锁脚锚管剪应力进行计算，可得锁脚锚管的最大拉拔力P0max=421.27 kN，进一步计算出锁脚锚管端部强度σmax=114.89 GPa.通过对比分析，锁脚锚管的最大拉拔力P0max≥X0，锁脚锚管不产生轴向滑移；σmax≤[σ]=205 GPa，锁脚锚管不发生弯曲破坏，证明了其古顶隧道采用锁脚锚管参数是合理的.

4)锁脚锚管-钢拱架力学分析过程中，仅考虑了围岩膨胀性对钢拱架的作用力，并未考虑围岩膨胀性对锚管与围岩耦合下锚管剪应力和正应力的影响，因此需要进一步研究.