缓和曲线线型对悬挂式单轨车辆动力响应的影响
寇峻瑜,余浩伟,谢 毅,罗 圆,肖 杰
(1.中铁二院工程集团有限责任公司,成都 610031;2.四川高新轨道交通产业技术研究院,成都 610031)
缓和曲线是连接直线和圆曲线的一段曲率渐变的过渡曲线,在该范围内,车辆所承受离心力逐渐增大,缓和曲线的存在可保证列车在直线和圆曲线之间平稳、安全、舒适地过渡.文献[1]介绍了一种采用S型或C型缓和曲线连接两个圆曲线的方法.通常曲率的变化使得不同缓和曲线线型下的动力变化规律会有差异[2-3].文献[4]采用车辆动态曲线通过理论,针对准高速和高速铁路的研究指出,高次缓和曲线相比三次螺旋缓和曲线对改善旅客舒适度的意义不大.
悬挂式单轨作为一种新型轨道交通制式,车辆吊挂于轨道梁下方行驶[5],近年来受到广大科研工作者的关注.文献[6]以日本千叶线悬挂式单轨车辆为研究对象,对不同速度、走行轮侧偏刚度下导向轮径向力的动态变化规律进行了研究.文献[7-8]建立悬挂式单轨车桥耦合动力学模型,探讨了不同通过速度下的桥梁振动加速度、模态和关键结构参数取值.关于线路技术条件的研究,文献[9]采用静态分析手段提出了线路平纵断面主要技术参数取值和计算方法,未涉及缓和曲线线型.文献[10]从旅客舒适度角度,采用行驶动力学理论计算得出了悬挂式单轨最小平曲线半径和圆曲线长度.总体来看,对悬挂式单轨的研究多集中于车辆曲线通过性能、车桥耦合振动等,且线路参数方面以理论计算为主,针对车辆与线路之间的匹配关系的研究还很匮乏.
本文作者以国内车辆为例,基于多体动力学理论建立悬挂式单轨车辆系统动力学模型,研究在不同缓和曲线线型条件下,车辆动力特性的变化规律,研究成果可为悬挂式单轨线路参数选型及工程设计提供参考.
1 悬挂式单轨车辆动力学模型
1.1 车辆结构
悬挂式单轨系统主要包括车体、转向架、悬挂装置和轨道梁等,转向架涵盖了构架、驱动电机、齿轮箱、走行轮、导向轮和制动装置等.构架是整个转向架的承重机构,置于下部开口的箱型轨道梁内,其下端通过一个可绕轨道梁左右摆动的中心销与摇枕连接,中心销两侧各安装有一个抗摇摆减振器,用于衰减车辆运动中产生的横向振动;摇枕两侧与车体之间安装有空气弹簧悬挂装置,同时还配置有垂向减振器、横向减振器和牵引拉杆等,分别用于衰减振动及传递载荷.走行轮和导向轮均采用实心橡胶轮胎,分别实现走行和导向功能.悬挂式单轨车辆-轨道结构简图如图1所示.
1.2 动力学模型
根据车辆系统结构特点,在动力学仿真软件Universal Mechanism(UM)中建立图2所示的悬挂式单轨车辆-轨道系统动力学模型.
该模型中车体、构架、摇枕、轮胎和轨道梁均视为刚体,不考虑其弹性变形,并合理简化处理了车辆系统各部件之间的连接关系,总共25个刚体,60个自由度,系统各自由度见表1,表中“√”表示有该自由度.横向减振器、垂向减振器、抗摇摆减振器的非线性力学行为采用阻尼力跟速度正相关的黏弹性力元模拟,空气弹簧和牵引拉杆则考虑为线性力元.
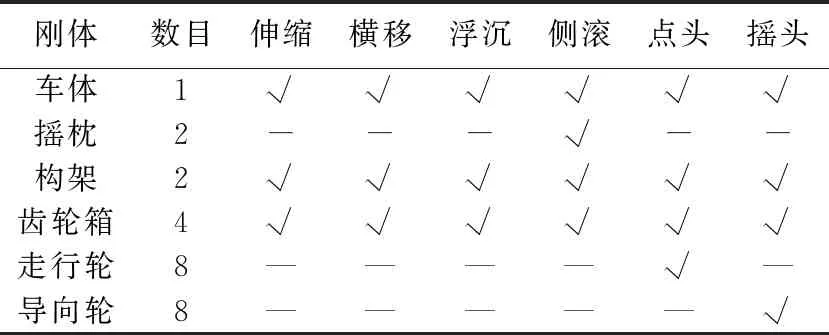
表1 悬挂式单轨车辆系统自由度
1.3 轮胎模型
由于走行轮和导向轮在轨道梁内运行时的侧倾角度较小,其与轨道梁之间的相互作用关系可采用Fiala轮胎模型描述.考虑到轮胎在走行过程中与轨道梁之间可能会产生间隙,故采取分段线性函数的方式来模拟轮胎与轨道间的径向力,可表示为
(1)
式中:kz、dz分别为实心橡胶轮胎径向刚度、阻尼;Δr为轮胎径向挠度;VΔr为轮胎的径向变形率.
车辆走行过程中轮胎的变形较小,轮胎各向刚度均考虑为线性,并忽略垂向载荷变化对走行轮胎各向刚度特性的影响,即忽略轮胎刚度非线性影响.
2 缓和曲线线型及施加方法
表2列出了目前世界上具有代表性的几种缓和曲线的方程式[11-12],如超高与曲率线性变化的三次抛物线;超高与曲率非线性变化的五次、七次和九次抛物线、半波和一波正弦.表中:y为纵坐标;k为曲率;l为缓和曲线上任意点距直缓点的长度,m;l0为缓和曲线全长,m;R为圆曲线半径,m;k0为圆曲线曲率,1/m.
由于三次抛物线具有线型简单、平立面有效长度长、现场运用、测试和维护容易等特点,在我国高铁、地铁等线路上得到广泛应用.理论计算表明,高次曲线型缓和曲线相比三次抛物线满足更多的几何和力学条件[11].但在实际施工过程中,由于轨道梁的加工制造精度,完全按照理论曲线施加的难度较大,多次样条曲线的实现存在一定困难.因此,采用动力学仿真手段对表2中各类缓和曲线线型工况下的舒适性指标和轮胎力进行研究,可为悬挂式单轨线路缓和曲线线型的选择提供数据支撑.

表2 铁路缓和曲线方程式
UM中默认的缓和曲线为三次抛物线,其他线型的实现需借助外部手段拟合.首先选取一定长度的缓和曲线,在横向上每隔0.5 m设置一个点,根据表2中各类线型的方程式可计算出点对应的纵坐标,将横、纵坐标取值导入AutoCAD即可绘出相应线型的缓和曲线,根据曲线半径绘制圆曲线,最后将设定曲线的离散点导入UM,即可完成不同线型的模拟.为验证该方法的可靠性,通过其模拟的三次抛物线与UM默认线型条件下的车体横向偏角对比如图3所示,两者基本吻合.
3 缓和曲线线型的影响
悬挂式单轨车辆通过曲线时,车体受到的作用力主要有中心销拉力、自身重力以及离心力.由于空气弹簧和减振阻尼的约束作用,车体的横向倾摆不能完全抵消产生的离心力,会存在部分未被平衡的离心加速度.通常舒适度的好坏,既能说明旅客的乘坐体验,也能反映出列车与线路之间的相互作用.在平面线路设计中,车体横向偏角及其时变率、车体未被平衡离心加速度及其时变率是乘客舒适度的评价指标[13].故主要基于此来探讨悬挂式单轨车辆通过不同缓和曲线线型工况时动力响应的变化规律.
首先设定线路条件:缓和曲线长150 m,圆曲线半径为600 m,圆曲线长900 m,运行速度按最高设计速度80 km/h考虑;轨道梁不设超高,曲线考虑为线路走行方向的左转弯,同时在导向轮与导向轨面之间施加一定数值的预压力.鉴于不平顺激励产生的随机振动会掩盖线路曲率转折点处的振动特性变化规律,不考虑轨道梁不平顺,主要研究车辆稳态通过曲线.
3.1 线型对旅客舒适性指标的影响
不同缓和曲线线型条件下车体横向偏角的时程曲线如图4所示,图中也示意了直线、缓和曲线和圆曲线的分布位置.在缓圆点和缓直点附近,不同线型下的车体偏角均存在一个显著的低频振动,其主要跟单轨车辆曲线通过特性有关,但振动起始点和幅值存在差异.三次、五次、七次和九次抛物线、半波和一波正弦条件下的偏角结果分别于18.93、17.87、17.55、17.09、17.84 s和17.41 s时刻开始出现波动,缓圆点对应时刻为18 s,因此,除了三次抛物线,其余线型下偏角起始振动点均出现在车辆驶入缓圆点前,其中九次抛物线最先产生该现象,缓直点附近的结果同理.由此表明,高次曲线型缓和曲线的阶次越高,缓和曲线的有效长度就越短.
三次、五次、七次和九次抛物线、半波和一波正弦条件下的横向最大偏角分别为5.40°、4.85°、5.38°、5.83°、4.92°和5.56°,九次抛物线的结果最大,相比三次和五次抛物线分别增大了7.96%和20.21%.当缓和曲线为五次抛物线和半波正弦时,车体偏角的振动衰减周期数最少,约2~3个,三次抛物线约5~6个,七次、九次抛物线和一波正弦约6~7个,表明五次抛物线和半波正弦工况下的车体横向晃动最快趋于平稳.由于车辆通过左曲线时,车体倾摆方向相反于横向正方向,偏角结果为负值,其中负号仅代表方向.
对图4中偏角数据求导后可绘出图5所示的偏角时变率结果.由于线路未设超高,偏角时变率可类比于传统轮轨铁路中的超高时变率.偏角的振动特性使得偏角时变率也会产生周期性的波动,其中三次抛物线的偏角时变率最大值出现在约1/4长的缓和曲线处,其他线型则靠近缓和曲线中点.虽然五次抛物线和半波正弦的最大偏角小于三次抛物线,但两者的偏角时变率最大值相较三次抛物线更大,主要原因是高次曲线型缓和曲线曲率导数的最大值一般在中点位置,由于其有效长度较短,未能有效降低曲率导数的最大值.三次、五次、七次和九次抛物线、半波和一波正弦条件下的偏角时变率最大值分别为1.28 °/s、1.53 °/s、1.95 °/s、2.35 °/s、1.58 °/s和2.10 °/s,九次抛物线的结果相比三次抛物线增大了83.59%.另五次抛物线和半波正弦型缓和曲线对应的偏角时变率的衰减速率明显快于其他线型,这与偏角结果相一致.
由线路条件决定的车体未被平衡离心加速度及其时变率也是重要评判指标.图6给出了不同线型下车体未被平衡离心加速度的时程曲线.三次抛物线的未被平衡加速度最大值出现在缓直点后,七次和九次抛物线、一波正弦的加速度最大值在缓直点前,而五次抛物线和半波正弦在缓圆点后.三次、五次、七次和九次抛物线、半波和一波正弦条件下的加速度最大值分别为0.053、0.054、0.069、0.093、0.055 m/s2和0.074 m/s2,九次抛物线的结果相比三次抛物线增大了75.47%.其中,三次和五次抛物线、半波正弦的加速度最大值相差很小,但三次抛物线条件下加速度的衰减周期数明显多于五次抛物线和半波正弦.因此五次抛物线和半波正弦型缓和曲线条件下的人体舒适度体验相比三次抛物线会更优.
若未被平衡离心加速度的变化率过快或者不连续,也将对旅客的乘坐舒适性产生较大影响.未被平衡离心加速度时变率不仅可以作为评价线路线型的指标,也可用于量化舒适性指标.对图6中未被平衡离心加速度求导后可得到相应加速度时变率的曲线如图7所示.三次、五次、七次和九次抛物线、半波和一波正弦条件下的加速度时变率最大值分别为0.069、0.037、0.080、0.122、0.039 m/s3和0.096 m/s3,九次抛物线的结果最大,相比三次抛物线增大了76.81%,五次抛物线和半波正弦的结果最小,相比三次抛物线分别减小了46.38%和43.48%.
结合图6和图7中未被平衡离心加速度及其时变率的变化趋势,同一振动衰减周期内,七次和九次抛物线、一波正弦3类工况下的横向晃动幅度最大,五次抛物线和半波正弦最小;同一时间段,五次抛物线和半波正弦对应的振动衰减速率最快,这与偏角时变率的变化规律一致.因此,一个时段内车体来回晃动的幅度过大或频率过快相比各舒适度指标的最大值会更不利于旅客舒适性,五次抛物线和半波正弦型缓和曲线要更优于三次抛物线和其他高次缓和曲线.
3.2 线型对轮胎力的影响
不同线型条件下的轮胎径向力如图8所示.根据图8(a)中走行轮垂向力数据,九次抛物线的垂向力最大值最大,五次抛物线和半波正弦最小;垂向力在缓圆点和缓直点附近也出现了低频波动,九次抛物线波动幅度最大,七次抛物线和一波正弦其次,然后是三次抛物线,五次抛物线和半波正弦条件下的波动最小且衰减最快.不同线型工况下的导向轮导向力如图8(b)所示,各线型对应的结果无较大差别.
基于走行轮垂向力,可得到图9中第一位轮对轮重减载率(所有轮对中结果最大)的时程曲线.九次抛物线的轮重减载率最大值为0.23,是所有线型中最大的,七次抛物线和一波正弦次之,为0.22,三次抛物线为0.20,五次抛物线和半波正弦最小,为0.19.
综上,悬挂式单轨车辆以速度80 km/h通过不同线型的缓和曲线时,高次缓和曲线工况的一些动力响应会大于三次抛物线,原因在于高次缓和曲线曲率导数的最大值在缓和曲线中点,使得缓和曲线有效长度更短,未能有效降低曲率导数的最大值.文献[11]中针对传统轮轨铁路缓和曲线线型的研究表明,当行车速度较低时,高次抛物线相比三次抛物线并没有太大优势,这与本文各动力响应的变化趋势一致.考虑到悬挂式单轨车辆的最高运行速度一般不大于80 km/h,三次抛物线相比高次缓和曲线更能发挥出有效长度更长的优势.由于缓和曲线长度对舒适性指标的影响较大,不同缓和曲线长度和速度下的动力响应变化规律,还需进一步深入研究.
4 结论
1)由于阶次越高的缓和曲线对应的有效长度越短,九次抛物线、一波正弦、七次抛物线、半波正弦、五次和三次抛物线会先后在缓圆点和缓直点附近产生低频振动现象.
2)理论上高次曲线型缓和曲线的力学性能更优,但对于速度较低的悬挂式单轨,高次缓和曲线相比三次抛物线并没有绝对优势,仿真与理论分析结果有一定差异.
3)相比车体横向偏角及其时变率、未被平衡离心加速度及其时变率等指标的最大值,其在同一振动衰减周期内的横向晃动幅度对旅客舒适性的影响更大,得益于较快的衰减周期数和较小的晃动幅度,五次抛物线和半波正弦型缓和曲线的动力特性更优于三次抛物线和其他高次曲线型缓和曲线.

