从齐次核向非齐次核发展的Hilbert 型积分不等式的研究进展

洪勇

（1.广东白云学院 数学教研室， 广东 广州510450； 2.广东财经大学 统计与数学学院， 广东 广州510320）

0 引言

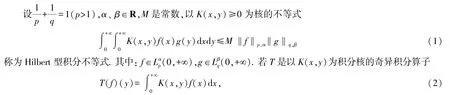
根据Hilbert 型积分不等式的基本理论，式（1）等价于

文［1］对近百年来，齐次核的Hilbert 型积分不等式的研究进展与现状进行了详细论述. 从中可以看到齐次核的Hilbert 型积分不等式研究由浅入深、由具体到抽象的发展历程和所取得的丰硕成果. 另一方面，伴随着齐次核情形的研究，各种非齐次核情形的讨论也同时展开，并也取得相应的研究成果（见［2－10］）. 本文对从齐次核到非齐次核Hilbert 型积分不等式理论的发展，论述其研究脉络.

1 两种重要的非齐次核

若函数K（x，y）满足条件：对t＞0，有K（tx，ty）＝tλK（x，y），则称是λ阶齐次函数.最早的Hilbert 积分不等式［11］

都是齐次核的情形，其中的常数因子都是最佳的.

齐次核情形的Hilbert 型积分不等式的讨论相对容易，非齐次核的情形，其研究难度则要大很多.多年的探讨，主要对下面的两类非齐次核取得较好的成果，形成了完整的理论体系.

一是设λ1λ2＞0，G（u，v）是λ阶齐次函数，令

一般地K（x，y）不是齐次函数，只有当λ1＝λ2＝λ0时，K（x，y）是λλ0阶齐次函数.我们称K（x，y）为具有参数（λ，λ1，λ2）的拟齐次函数.显然K（x，y）＝G（xλ1／yλ2）是具有参数（0，λ1，λ2）的拟齐次函数.拟齐次函数具有如下性质：t＞0 时，有

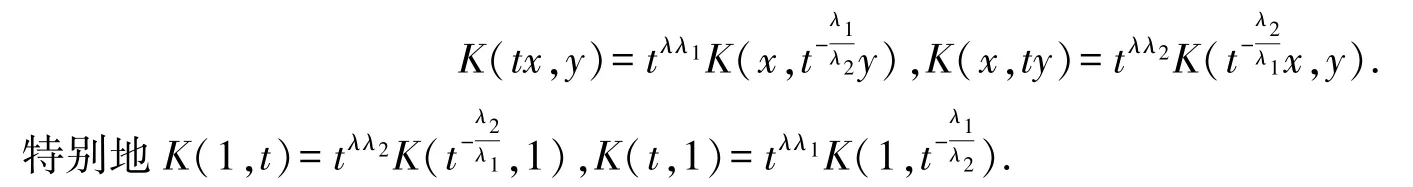
二是设λ1λ2＞0，若K（x，y）＝G（xλ1yλ2），则K（x，y）一般都是非齐次函数.对此类非齐次函数，显然它具有性质：t＞0 时，有

2 若干非齐次核情形的Hilbert 型积分不等式

随着权函数方法的创立，在研究齐次核的同时，人们也对一些具体的非齐次核Hilbert 型不等式进行探讨，通过选取适当的搭配参数a、b，获得许多优美的具有最佳常数因子的不等式.

以上这些不等式的常数因子之所以都是最佳的，其原因在于作者对搭配参数a、b进行了精心的选取.若随意选取搭配参数，则所得常数因子一般不会是最佳值.

作者根据自己丰富的经验选取了适当的搭配参数后，还需利用各种实分析技巧对权函数进行估算.因此每得到一个这种非齐次核的最佳Hilbert 型积分不等式往往都比较艰难.

3 最佳搭配参数的充要条件

选择搭配参数a、b，根据Hölder 不等式，利用权函数方法，可得

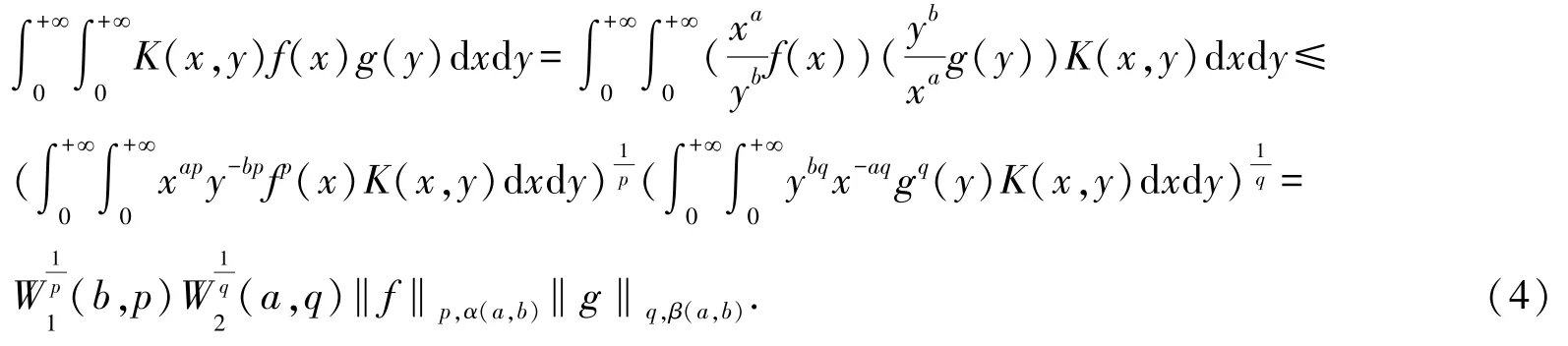
其中：α（a，b）及β（a，b）是与a，b相关的两个数，而

对于某种特征的核，讨论其最佳搭配参数a、b所满足的条件对于Hilbert 型积分不等式理论显然具有重要意义.例如当K（x，y）是拟齐次核或K（x，y）＝G（xλ1yλ2）（λ1λ2＞0）的非齐次核时，a和b为最佳搭配参数的条件是什么呢？ 若能找到其充要条件，就能够构造出无穷无尽的此类核的Hilbert 型不等式，从而对Hilbert型不等式的研究将进入一个新的阶段.通过对大量文献的分析，借鉴齐次核情形的讨论方法，我们得到了如下的两个定理.

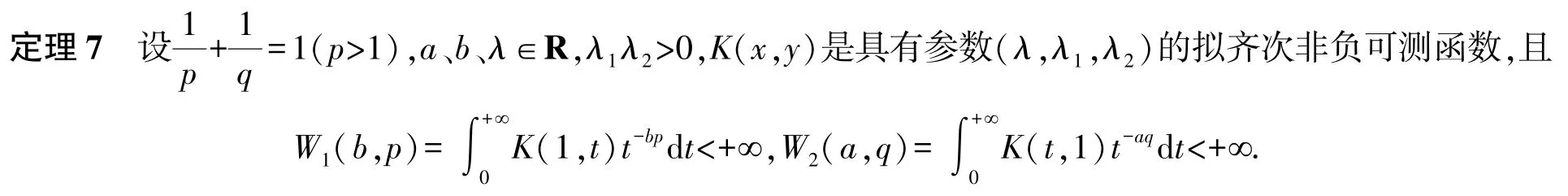
那么

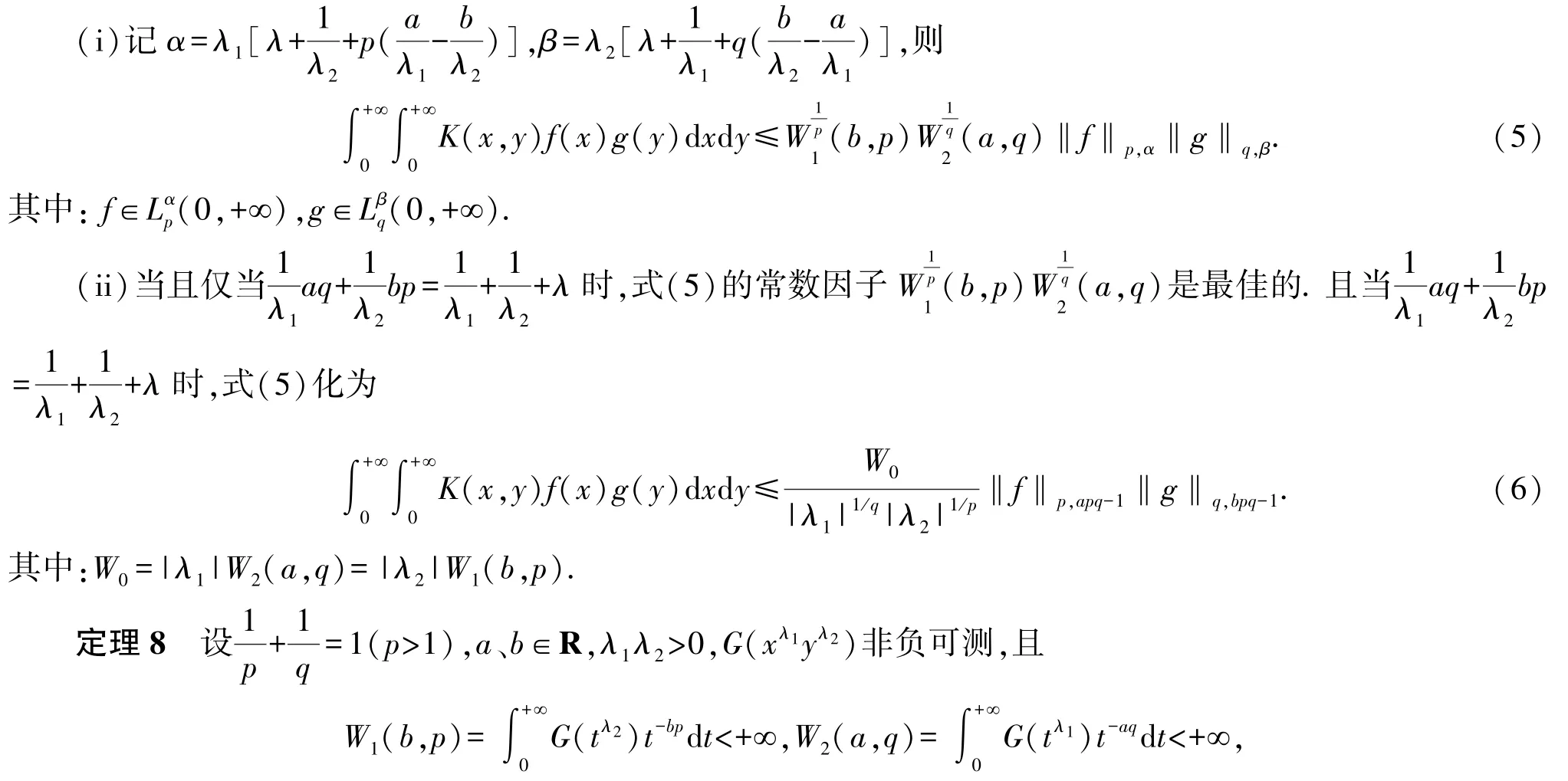
那么

其中：W0＝｜λ1｜W2（a，q）＝｜λ2｜W1（b，p）.

注：定理7 和定理8 的证明将在另文中给出，在此不祥述.

若是我们令

则式（5）的常数因子最佳的充要条件是Δ1＝0； 式（7）的常数因子最佳的充要条件是Δ2＝0.今后称Δ1是式（5）中a、b为最佳搭配参数的判别式； Δ2是式（7）中a、b为最佳搭配参数的判别式.其中的常数因子是最佳的.

根据定理7，式（9）成立，且其常数因子是最佳的.

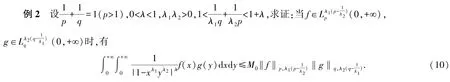
其中的常数因子

是最佳的.

故a、b是最佳搭配参数.又因为

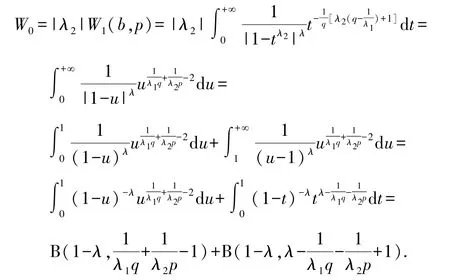
根据定理8，知式（10）成立，其常数因子是最佳的.

4 构建Hilbert 型积分不等式的参数条件

前面已经解决了选取最佳搭配参数的问题，将Hilbert 型不等式的研究推向一个新的阶段.进一步，我们应该考虑的是在什么参数条件下可以构建Hilbert 型不等式？ 例如当K（x，y）是具有参数（λ，λ1，λ2）的拟齐次核时，参数λ、λ1、λ2、p、q、α、β在什么情况下存在常数M＞0 使式（11）成立？

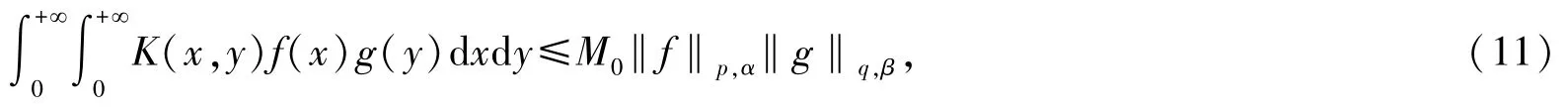
且当式（11）成立时，其最佳常数因子M0＝infM是什么？ 这样的问题实际上就是由式（2）定义的算子T何时有界及如何求算子范数的问题.

目前，这些问题得到较好的解决，详见定理9 和定理10.

收敛，那么

（ii）当式（12）成立时，其最佳常数因子为

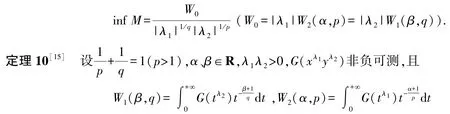
收敛，那么

（ii）当式（13）成立时，其最佳常数因子为

其中的常数因子

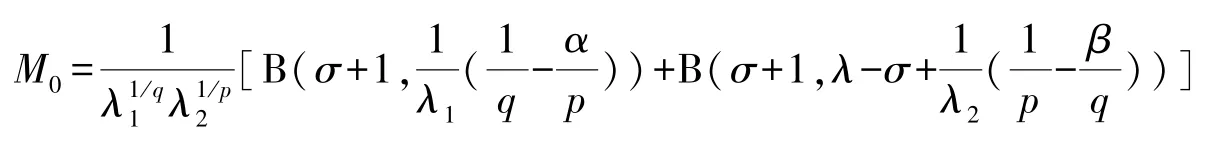
是最佳的.

根据定理10，知本例结论成立.