基于机器人操作系统和向量场直方图的自动导引车快速部署方案设计

李泽寰，肖美华

(华东交通大学软件学院，江西 南昌 330013)

随着机器人技术逐渐成熟且成本降低，越来越多公司开始使用工业机器人进行生产，以提高产能，首先就是对自动导引车(Automated Guided Vehicle，AGV)的使用。AGV属于一种移动运输机器人，在工业上应用广泛，但是普通AGV在应对环境改变时不能做出良好的反应，并且AGV产品在进入生产车间或其它工作场所后需要专业人员进行专业调试，极大影响了工厂产品生产，亟需增强AGV的环境适应能力以及缩短AGV进厂测试时间。在当前工厂环境下，AGV部署存在以下问题：1.AGV进厂工作后需要专业人员进行测试和调试；2.灵活性较差，如果工厂需要对生产环境进行改变,需要专业人员对AGV进行调整；3.市场上大规模使用的电磁导引和磁带导引AGV虽然可靠性高，但是需要对场地进行大规模改造，并且需要定时对场地进行维护；4.市场上普遍使用的AGV光学引导方法对场地的光学环境要求较高。上述问题终究是AGV自动化不足的问题，许多开发人员为了增强AGV自动控制能力，通常使用即时定位与建图算法(Simultaneous Localization And Mapping，SLAM)来实现智能AGV对环境的适应[1]。SLAM是如今常用的一种导航和建图方法，SLAM可以通过激光雷达或深度摄像头准确构建地图[2]，极大提高了机器人的环境感知能力，但是SLAM需要大量的硬件资源作为支撑，而且现实情况下的工厂环境相对简单，并不需要构建一张如此详细的地图，SLAM构建地图的速度也过于缓慢，这不利于AGV的快速部署。

工厂环境下需要的是一种低资源且高效可靠的运动规划和建图算法。向量直方图法(Vector Field Histogram，VFH)是Johann Borenstein和Yoram Koren提出的一种实时运动规划算法[3]。VFH算法的主要思想是量化机器人当前时刻各方向与障碍物的距离，根据量化出的障碍物强度值得出最优运动方向[4-6]。拓扑地图是一种描述点与线关系的地图，其忽略大量的环境细节，能紧凑地表示AGV所在的环境信息[7]，正因如此，建立拓扑地图所需要的硬件资源和计算力较小。

本文组织结构如下：第1节介绍AGV软件系统的总体设计，优化VFH算法用于计算最优行驶方向；第2节构建拓扑地图，应用于AGV运动控制中；第3节对VFH+拓扑地图的方案进行验证，分析AGV生成的节点信息，验证结果表明该方案可以满足AGV的快速部署；第4节为本文的结语。

1 基于VFH算法的运动规划

1.1 总体设计

本研究目标是使得AGV在室内可以自动规划路径并同时构建拓扑地图，从而实现快速部署。在室内，AGV面对地通常是相对固定的环境，所以使用激光雷达作为感知传感器；激光雷达与惯性测量单元(Inertial-Measurement Unit,IMU)结合为自动导引车提供最优路径与全场定位[8]。

AGV系统包含上位机和下位机两个部分。下位机由单片机(STM32F103)、IMU(MPU6050)、码盘组成 ，用来控制AGV的运动，其中IMU与STM32使用IIC进行通信；上位机由激光雷达和嵌入式开发板(Jetson Tk1)组成，用来规划AGV的运行方向。上位机是基于ROS开发的，上位机通过串口与下位机、激光雷达通信，如图1。AGV软件系统整体设计流程如图2。

1.2 动态路径规划

本文采用VFH算法对AGV进行动态路径规划。VFH算法的核心思想是以移动机器人为中心建立极坐标系，将障碍物对AGV的影响量化为AGV在每个极坐标方向上的障碍物强度，以此构建AGV在此位置的向量直方图[9-12]，如图3；向量直方图可以反映出AGV周围的环境情况，通过在向量直方图中设置阈值可以判断出AGV的可通行方向。在软件设计上，首先要做得是计算障碍强度值。障碍强度计算公式如式(1)。

(1)

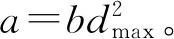
针对距离阈值dth计算出障碍强度阈值M，M的取值关系到AGV的运行方向；在VFH算法中，选择障碍强度值小于M值的方向作为备选方向，所以如果M值较大，可以较早的发现障碍物及时调整方向，如果M值较小可以提高备选方向的可靠性，使得AGV可以向着更安全的地方行驶，但是这样会容易导致AGV进入“死区”。因为AGV工作的环境相对稳定，所以为了得到合适的阈值， AGV在可能需要通过的最窄路径上测量四周的障碍强度值并观测向量直方图，在向量直方图中选取最佳阈值。障碍强度值二值化处理求得可通行扇区直方图，以此简化数据处理难度，如式(2)与图4。

(2)

经过二值化处理后，障碍强度值为0的方向为可行驶方向，把求出的所有可行驶方向称为集合A，但是集合A中的候选可行驶方向依然太多，不能指出最优行驶方向，为此引入代价函数[13-15]，求出各候选方向的代价值，代价最小的为行驶方向，如式(3)

g(c)=μ1Δ(c,kt)+μ2Δ(c,kr)+μ3Δ(c,kb_pre)

(3)

在式(3)中，c为候选行驶方向，Δ(c,kt)为候选方向与目标方向的夹角，Δ(c,kr)为候选方向与机器人当前方向的夹角，Δ(c,kb_pre)为候选方向与上一次运动方向的夹角。μ1、μ2、μ3为常数且满足μ1>μ2+μ3。比较各候选方向的代价值，代价值最小的为最优行驶方向。

上述方法求出的最优行驶方向有图5所示问题，图中箭头所指的AGV最优方向是没有障碍物的，但是因为AGV自身长宽影响，AGV无法通过这个路口，这是因为代价函数没有考虑候选方向、AGV自身长宽、障碍物三者间的关系。

为了避免在AGV长宽影响下得出错误的候选方向，本文提出一种关联相邻方向的方法来剔除无效方向。如图6，候选方向向左偏移θ得到左偏方向，同理得到右偏方向，计算候选方向与左右偏移方向之间存在的方向有多少存在于集合A中，如果左边(右边)存在于集合A中的方向小于3θ/5个，或者左偏方向(右偏方向)不在集合A中，那么此候选方向无效，不应该和其它候选方向进行代价比较，如式(4)。剔除集合A中的无效候选方向后，再进行代价值计算，代价值最小的方向为最优行驶方向，可以成功的避开障碍物，如图7。

(4)

&&fL(θ)=1&&fR(θ)=1⟹Valid

2 基于拓扑地图的建图方法

2.1 拓扑地图的建立

拓扑地图是一种保持点与线相对位置关系而不必保持图形形状的抽象地图[7,16]。

在本研究中，AGV在探索周围环境时自动生成拓扑节点，节点中包含此时AGV的全局坐标和下一时刻的运动方向，在AGV探索完成周围环境后产生的所有节点构成拓扑地图。AGV在起点调用拓扑地图，根据拓扑地图上的信息，AGV可以在相邻节点间移动。图8为实验场所示意图。

在图8所示环境中，AGV可以生成四个节点，设这四个节点为a、b、c、d，拓扑地图为图9所示。

节点中包含此点的全局坐标、此点与相邻节点的方位信息和此时速度，AGV正常工作时就检索储存的节点，根据节点信息AGV可以获取移动到下一点处需要的参数。拓扑地图符号化为G=(V,E)，其中节点集合表示为：

V={a,b,c,d}

连接节点的边的集合表示为：

E={(a,b),(b,a),(b,c),(c,b),(c,d),(d,c)}

拓扑节点的生成是通过判断AGV行驶方向突变程度的高低。如图7的拐角，AGV需要左拐进入一条新的通道；在此环境下，AGV偏左的方向必然比其它方向更加空旷，因此计算系统得出下一刻行驶角度将在此刻行驶方向上向左偏，环境中拐角越大，两个时刻间的偏移量就越大，根据以上规律得出生成拓扑节点的基本原理为：通过偏移量的大小判断是否到达关键节点。关键节点在存储到ROM前需要和已确定的节点进行模板匹配，确保存储的节点为新节点。如式(5)。

φ=vfh_aimR-vfh_aim_N

(5)

式(5)中，vfh_aimR是当前行驶方向，vfh_aimN为下一刻行驶方向，φ为偏移量，Q为一常量，point是采集到的节点，Points是拓扑节点集合，ma表示新得到的节点在节点集中进行匹配，ma(point)=1表示匹配成功，此节点为旧节点，ma(point)=0表示匹配失败，此节点为新节点。

2.2 拓扑地图的使用

为了便于控制，引入邻接矩阵来表示点与边的关系，当AGV需要从拓扑地图中的一个节点移动到另一个节点时，只需要改变邻接矩阵中的参数，邻接矩阵的行列由拓扑地图决定。在本研究环境里，取4×4邻接矩阵AG，通过给各条边赋予不同的权值来区分行驶方向和阻碍方向，这里将行驶方向的权值设为2，阻碍方向的权值设为1。

(6)

如式(6)所示的邻接矩阵表示了AGV从节点a移动到节点d的一个过程：AGV从a开始运动，先移动到b再从b移动到c，从c移动到d，在d停止运动。拓扑地图与邻接矩阵的结合使得AGV复杂的运动控制抽象为简单的参数修改，从而实现AGV在建立完成地图后，工作人员可以快速定义AGV的行驶路线。

邻接矩阵设置AGV可行驶方向，而在控制细节上，由复合PI控制器来实现AGV在极坐标上的行进和转向，具体流程为：邻接矩阵决定AGV行驶方向，复合PI控制器接收邻接矩阵对应的拓扑节点信息，在控制器收到节点信息后，AGV先转到命令角度，再向着这个角度前进。如此控制模式的好处就是，上位机只需修改此时邻接矩阵的信息，就可以控制AGV的运动，这种方法降低了上位机与下位机的通信成本和控制复杂度。控制器实现如式(7)。

(7)

BiasL=EncoderL-left

BiasR=EncoderR-right

left_pwm+=P×(BiasL-Last_biasL)+I×BiasL

right_pwm+=P×(BiasR-Last_biasR)+I×BiasR

式(8)中，left与right为左轮和右轮的目标转速，angle为当前航向角和目标角度的间隔，EncoderL与EncoderR为当前左轮和右轮的转速，BiasL与BiasR为当前电机转速和目标转速的差值，left_pwm与right_pwm为左右轮的pwm值。

3 实验与验证

3.1 节点坐标转换

节点坐标的精准度决定AGV是否能安全运行，VFH算法是通过激光雷达的数据来决定AGV的行驶方向，但是激光雷达的数据是以局部角度输出的[17-18]，如图10(a)，为此需要把激光雷达的角度信息与IMU测出的姿态参数进行转换，得出激光雷达对应的全局极坐标角度，也就是集合A里的候选行驶方向。IMU测出的姿态参数为航向角、横滚角、俯仰角，在这里只需要使用航向角，利用航向角建立极坐标如图10(b)所示。

激光雷达角度转换为全局极坐标角度的原理为：一组环形序列映射到极坐标上后，再加上IMU上的AGV偏移量，如式(8)。

Global=yaw+Lida

(8)

式(8)中，Lida为激光雷达的角度，yaw为IMU测出的航向角，Global为激光雷达转换后的角度。经过式(7)的计算，激光雷达的角度转换为了全局极坐标角度。

3.2 生成节点

本研究中使用Nvidia的Jetson TK1嵌入式开发板作为AGV的上位机，下位机使用了STM32F103ZET6开发板，激光雷达选用了HLS-LFCD2激光雷达，IMU使用的是MPU6050，串口模块使用了CP2102 USB转串口模块，电机为减数比30的带编码器电机，图11为团队开发的AGV。

实验环境为图8所示，此环境得到的节点数据为表1。表1中的数据为节点全局极坐标映射出的全局直角坐标，通过数据点可以获得AGV的运动轨迹和各节点时的运动状态。

表1 节点数据

表1的结果表示4个节点可以抽象出该环境，节点1为初始节点，它的方向没有被记录，一般来说，初始节点的方向为0或者通过节点2的位置求出；节点4为终止节点，因为AGV在节点4停止探索，所以节点4方向设为0。利用表中的节点数据，AGV在图8中的环境下可以快速移动到任意目标节点。

本文与文献[1]比较。文献[1]使用了基于3D Orbbe摄像机的视觉SLAM方法为机器人导航，构建的地图如图12所示。

此地图比较详细地展现出测试场地的环境，但是相对的，高精度往往伴随着建图的低速度和高资源消耗。文献[1]使用配置为i5 CPU、8GB RAM、GTX970显卡的个人电脑实现视觉SLAM，并且为了实现物体的识别，花费了7天的时间训练模型；所以和视觉SLAM相比，本文提出的AGV快速部署方案更能在低资源的情况下，把AGV快速部署到工厂。

4 结语

本文为解决AGV快速部署问题设计了一种新的建图方案。该方案以VFH算法为基础进行路径规划，在VFH算法中加入AGV自身大小约束，确保AGV可以通过各障碍物，AGV探索四周环境时生成拓扑节点形成拓扑地图，最终通过拓扑地图部署在固定场地。控制方面，建立极坐标系，以输出角度的方式控制AGV的行驶方向。实验结果表明该设计方案可行且高效，可以满足预期要求，但AGV建立节点的方式过于单一，节点只能表示环境中的岔口和拐点，未来的工作将把重点放在如何增加节点信息多样性方面。