基于傅里叶曲线拟合的水下目标运动要素解算方法∗

（91388部队41分队 湛江 524022）

1 引言

目前对水下目标的常见探测手段一般有磁异常探测法、声学探测法等，水面舰船平台对水下潜艇等目标进行探测跟踪时，多采用声纳设备。受限于水下声学探测设备的自身探测精度及复杂水声环境，对水下目标的探测跟踪数据往往具有误差大、易跳变等特点[1]。若直接使用探测数据进行目标运动要素解算，则会放大因探测手段、水声环境带来的误差，导致目标航向、航速解算值跳变。鉴于傅里叶展开式收敛性及对曲线数据的拟合度较好，本文提出利用基于傅里叶曲线拟合算法水下目标运动要素解算方法。

考虑到系统误差可以通过统计计算补偿，而随机误差一般均匀分布在真值两侧，利用基于傅里叶展开式的拟合算法，将测量值的离散点拟合至傅里叶展开式，进而求取更准确的目标运动要素。

2 傅里叶曲线拟合算法

曲线拟合就是根据测得的离散数据点，用解析表达式y=f(x,c)逼近离散数据点，用y=f(x,c)来反映变量x与y之间的依赖关系，即在某模型下“最佳”的逼近拟合已知的离散数据。一般是计算参数c使得拟合模型与实际观测值在各点的残差ek=yk-f(xk,c)的加权平方和达到最小。傅里叶曲线拟合算法就是建立基于傅里叶展开式的曲线拟合函数，利用拟合曲线上的点替代原始测量数据点，用于对目标的各运动参数进行分析计算。

图1 曲线拟合流程示意图

2.1 水下机动目标测量模型

机动目标在水下的运动测量轨迹往往是非线性的[4]，受限于水下探测手段的特点，测量值与实际值关系如下：

W与V分别代表过程噪声和测量误差，数学期望均为0，方差分别为Q、R，x、y代表观测值，且W与V非线性相关。

利用非线性函数的泰勒展开，将系统模型截断至二次项，忽略其余高阶项，相比一阶线性化截断可有效减少由于线性化引起的估计误差。

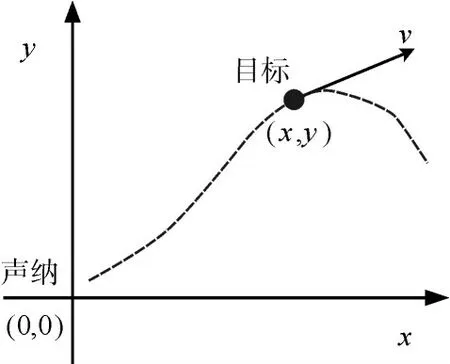
图2 目标运动示意图

2.2 运动轨迹傅里叶拟合算法及流程

通常目标运动状态是连续的或者相对稳定的，传感器对目标信息采样后形成离散点，利用目标时间、方位、距离、径向速度等元素构成目标运动状态矩阵。以声纳位置和时间为基准，对距离、方位构成的目标位置点进行坐标换算，使之成为高斯坐标点。将转换后的点按照傅里叶公式（本文选取3阶）进行拟合，拟合后得到连续的目标轨迹函数[7]。取任一时刻的轨迹函数的导数，则可得到此刻的目标运动参数。

傅里叶3阶拟合公式如下：

3 目标运动要素解算

水下目标的运动状态主要由位置、速度V、航向C、加速度a等决定，数据进行傅里叶拟合后的运动要素计算如下式：

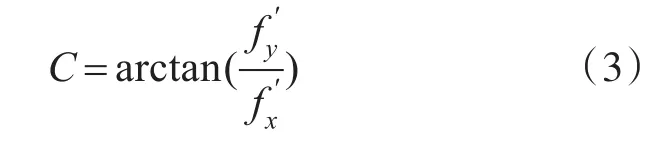
式中f'表示拟合函数的导数。

拟合流程如图3。

图3 滤波处理流程图

4 试验仿真及分析

为对上述算法性能进行分析验证，使用Matlab工具模拟水下目标航迹，并通过加入随机观测误差Ri（W、V）的方式来模拟实际的测量值zi（x、y）。假设水下目标初始段航向30°，末段做120°的机动旋回。数据采样周期为20s，采样点数为80点，测量噪声误差 ≤0.5。

滤波前目标理论轨迹与模拟测量轨迹如图4。

图4 目标轨迹图

对测量值zi（x、y）拟合处理后的轨迹图如图5。

通过计算系统模拟测量值zi及目标理论轨迹一次差及拟合处理后的拟合残差，滤波前的一次差如图6。拟合处理前轨迹测量值的二阶原点距约为0.41，拟合处理后目标轨迹的二阶原点距约为0.15（中段15点统计值）。模拟目标探测数据拟合处理后，目标轨迹的二阶原点距比拟合处理前减小了约65%，目标运动要素解算精度提高约58%。通过试验，表明此方法可有效降低因观测误差导致的水下目标轨迹跳变大的影响，同时可有效提高轨迹测量精度，减小水下目标运动要素的解算误差，为后续数据处理提供支持。

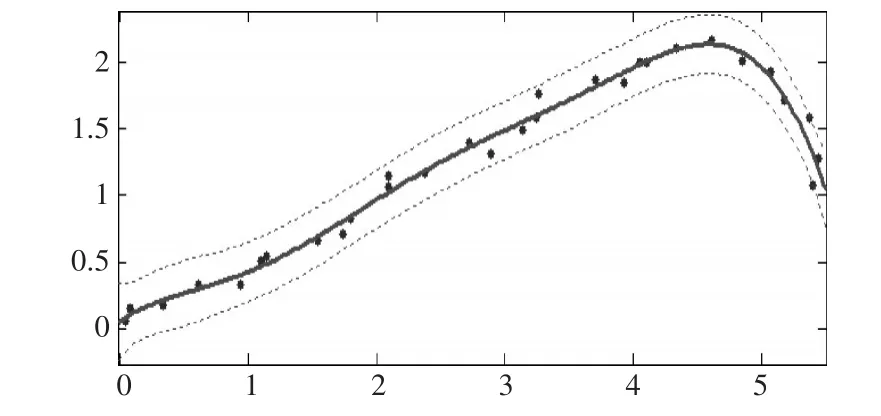
图5 曲线拟合后目标轨迹图

图6 模拟数据一次差

图7 曲线拟合后残差

5 拟合方法限制

图8 高机动目标轨迹重叠区

根据模拟数据计算发现，在目标做小旋回半径的大幅度机动时，目标探测数据误差与目标运动轨迹特征值接近。该情况将导致探测值出现重叠交叉，数据拟合过程中，拟合曲线易出现多个路径，以致出现错误结果。因此，此方法在处理大机动目标数据时存在明显限制，同时存在输出错误结果的风险。

6 结语

本文针对水下目标轨迹测量存在的观测误差大且运动非线性的特点，利用傅里叶拟合函数完成了水下目标运动要素算法设计。同时通过模拟实验分析，证明目标做简单机动航行时，基于傅里叶曲线拟合的数据处理算法能够很好地降低目标探测误差，可以较为准确地还原水下目标运动轨迹，同时可有效减小目标运动要素解算误差。但是这一方法并未考虑水下目标机动变深情况，另外，该方法在处理小旋回半径机动目标轨迹数据时存在明显限制。下一步将研究如何将此方法应用到水下目标三维运动轨迹的处理中。