基于随机摄动方法的广义随机复特征值问题研究
仇翯辰, 樊维超
(1. 中国商飞复合材料中心,典型结构部,上海 201324)(2. 中国商飞北京民用飞机技术研究中心,民用飞机结构与复合材料北京市重点实验室,北京 102211)
0 引言
20世纪90年代初期,邱志平教授将非概率不确定理论引入结构振动问题中,研究了不确定参数对结构固有频率的影响[1]。Ghosh将结构特征值和特征向量用混沌多项式(PCE)方法进行展开,开展了线性随机系统的不确定性分析[2]。
在进行实际工程结构的分析和设计优化时,当设计参数发生变化和扰动,结构力学行为(如固有振动特性)也会发生相应的变化,那么为了获得最优设计方案,迭代计算或者说反复的结构重分析是无法避免的。然而,对于大型复杂结构来说,诸如Monte-Carlo模拟和分层抽样等迭代计算方法的时间消耗是巨大的,计算成本过高。因此,能够进行快速灵敏度分析和结构重分析的矩阵摄动方法,便受到学者们的极大关注,近年来得到蓬勃发展。较高的计算效率和较少的时间消耗是矩阵摄动方法的显著特征,因此学者们纷纷投身于该领域的研究之中。陈塑寰系统地阐述了矩阵摄动理论在结构振动分析中的应用[3],在后来的著作中,陈塑寰又论述了结构动力学的矩阵摄动理论,开展了孤立特征值的摄动分析和线性振动亏损系统的矩阵摄动分析等研究[4]。考虑具有实特征值或者复特征值的随机结构,其特征值的统计量(如均值和方差)的计算对于结构的不确定性传播分析、动力学重分析和设计优化具有重要指导意义和参考价值。通过对不确定性传播进行准确的定量化,摄动之后实/复特征值的变化范围能够被准确地预测,那么摄动之后的特征值(或固有频率)和原设计使用工况之间的矛盾则能够被避免,这样结构系统的性能和可靠性将得到充分保障。对于传统的矩阵摄动理论,求结构随机特征值的统计量的常用方法是将刚度矩阵和质量矩阵在随机结构参数的均值附近进行Taylor展开,而随机特征值的方差由特征值的敏感度矩阵、随机结构参数的标准差矩阵和结构参数的相关系数矩阵求得。然而,在工程实际中,结构参数的相关系数矩阵是很难获得的,一般只能通过假设或者大量的样本统计试验获得,其成本极高,工程可实现性较差。因此使用传统的矩阵摄动方法进行不确定性传播分析受到了严重的制约,亟待建立一种改进的工程适用性强的矩阵摄动方法。
针对具有复特征值的随机结构系统,提出一种改进的不确定传播分析方法。通过该方法,在考虑结构参数不确定性的基础上,随机结构的复特征值的方差可以被方便地求出。
对于随机实模态结构,在之前的研究工作[6]中建立了一种改进的随机摄动方法来克服瓶颈。该方法将结构振动特征值和特征向量的一阶摄动展式与概率理论相结合,那么结构随机特征值的方差就可以由刚度矩阵的摄动项、质量矩阵的摄动项和原始特征向量直接推导出来。上述方法在对实模态结构随机特征值变化范围的计算中,不涉及结构参数的相关系数矩阵,在工程实际中是易于实现的。具体操作上,只需要知道随机结构参数本身的方差(或标准差),而不是结构参数之间的相关系数矩阵,这使得计算随机结构特征值的统计学性质变得更为便利。
实模态结构随机摄动方法被进一步改进并推广到复模态特征值领域。将改进的复模态结构随机摄动方法与概率理论相结合,推导出了随机复特征值方差关于随机结构参数的显式表达式。根据本文提出的方法,随机复特征值的方差能够由随机结构参数的统计量直接求出,那么相应的复模态结构的动力学重分析和不确定性分析也能够很方便地完成。值得一提的是,非对称系统也可能是亏损系统,换句话说,亏损系统中没有完备的特征向量系。在这种情况下,应用于非亏损系统的矩阵摄动方法将不适用于亏损系统,因此本文研究只针对非亏损系统。
1 复模态结构系统振动的基本方程
N维线性系统的复模态受迫振动方程可以表示为:
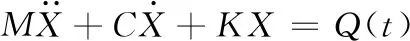
(1)
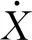
复模态结构系统的自由振动方程可以表示为:
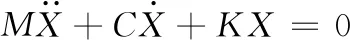
(2)
不妨假设X=xeλt,将其代入式(2),则获得相应的右特征值问题如下:
(Mλ2+Cλ+K)x=0
(3)
相应的伴随特征值问题为(Mλ2+Cλ+K)Ty=0,对伴随特征值方程进行转置,得到左特征值方程如下:
yT(Mλ2+Cλ+K)=0
(4)
其中向量x和y分别表示右特征值和左特征值,λ表示振动方程的特征值。
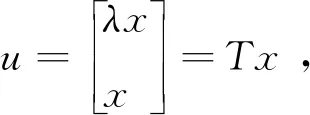
这样,式(3)和式(4)可以被分别改写为:
(Aλ+B)u=0
(5)
vT(Aλ+B)=0
(6)
其中

(7)
经过状态变换之后,式(2)可以改写为
(Aλ+B)u=0
(8)
以及
vT(Aλ+B)=0
(9)
式(8)和式(9)具有相同的特征值,均可以由以下方程求出:
det(Aλ+B)=0
(10)
式(10)是一个在复数域中具有2N个特征值的代数方程,这些特征值可以被表示为λi(i=1,2,…,2N)。考虑其中第i个特征值λi,其左状态特征向量vi和右状态特征向量ui均满足如下方程:
(Aλi+B)ui=0
(11)
viT(Aλi+B)=0
(12)
同时由特征向量的正交归一化条件有
vjTAui=δij
(13)
vjTBui=-λiδij
(14)
其中δij为Kronecker delta函数。
将u=Tx和v=Ty代入式(13)和式(14),得到下式:
同时注意到式(7),进一步将上式改写为:
yjT[M(λi+λj)+C]xi=δij
(15)
yjT[-Mλiλj+K]xi=-λiδij
(16)
式(15)和式(16)也被称为原二阶系统的模态正交化条件。
2 复模态结构振动的矩阵摄动方法
实际工程中,结构参数的变化是具体体现在质量矩阵、阻尼矩阵和刚度矩阵的变化之中的。考虑参数在其均值周围的小扰动,可以将质量矩阵、阻尼矩阵和刚度矩阵表示为:
(17)
其中ε是一个小参数,并且对于原始系统有ε=0;M0,C0,K0分别表示质量矩阵、阻尼矩阵和刚度矩阵的均值;εM1,εC1,εK1分别表示M0,C0,K0的一阶摄动项。进一步,式(13)和式(14)中的A和B可以表示为:
(18)
需要补充的是,本节讨论的是原始特征值为特征方程(10)中单根的情况。根据矩阵摄动方法,复模态结构振动系统的特征值和特征向量可以展成摄动级数的形式:
(19)
将式(19)和式(18)代入式(11)得到:
(20)
相似的,将式(19)和式(18)代入式(12)有:
(21)
展开式(20)并且忽略O(ε3)的项,比较等式左右两边ε同次幂项的系数得到:
(22)
对于式(21)进行同样的操作有:
(23)
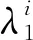
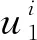
(24)
将式(24)代入式(22)得:
(25)
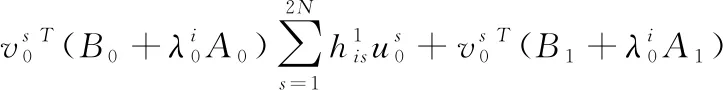
(26)
考虑式(13)和式(14)所表示的模态正交归一化条件,式(26)能够被简化为:
(27)
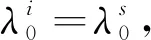
(28)
式(28)可以进一步改写为:
(29)
3 随机复特征值的不确定性传播分析
由于原材料性能的差异,制造加工的误差和载荷环境的变化,实际工程结构中的质量矩阵、阻尼矩阵和刚度矩阵一般被认为是随机结构参数。这样一来,便导致了随机结构中特征值和特征向量的随机性。
本文中,矩阵摄动方法被引入到具有随机参数的复模态结构的特征值分析之中,同时也为非对称系统的不确定性传播分析打下了基础。考虑结构参数的随机性质,刚度矩阵K,质量矩阵M,阻尼矩阵C,复特征值λi,左复特征向量y和右复特征向量x可以被表示为如下的形式:
(30)
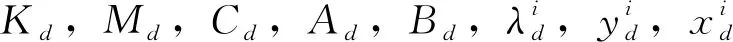
根据概率理论,对式中的各随机参数求期望,可以得到下式:
(31)
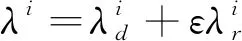
(32)
对式两边取期望算子,有
(33)
另外,复特征值λi的方差可以表示成如下形式:
(34)
在式(34)中,使用了复数/复向量方差的定义和期望的定义来完成推导。
将式(30)代入式(11),采用与第1节相同的方法,得到:
(35)

(36)
由式(36)可得
(37)
简便起见,下文的推导中将移除符号的上脚标i。同时,注意到只有特征值λd、左特征向量yd和右特征向量xd为复数形式,同时各个结构参数矩阵的一阶摄动项Mr,Cr,Kr均为实数矩阵。所以假设:
(38)
其中λdr,ydr,xdr和λdy,ydy,xdy分别表示λd,yd,xd的实部和虚部。
注意到E[Mr]=E[Cr]=E[Kr]=0,所以随机结构参数Mr,Cr,Kr两两乘积的数学期望均为零。因此,将式(35)和式(38)代入式(37),得到
Var(λr)=E[(λr)·(λr)H]
(39)
为表达式的简明起见,令:
(40)
将式(40)代入式(39)可得:
(41)
并且
(42)
值得一提的是,如果特征值λ∈R,则特征值和相应的左/右特征向量的虚部均为零,亦即,λdy=0,ydy=xdy=0,λd=λdr。因此,可以得到
式(42)将退化为:
(43)
显而易见,式(43)与随机结构的实特征值的方差表达式相一致。
4 数值算例
4.1 算例一:两自由度振动系统
一个二自由度的振动系统如图 1所示,该系统满足c=1,k=9,m=1,并且有c1=c2=c3=c。由达朗贝尔原理,得到该系统的运动微分方程

图1 两自由度振动系统
根据上式,右状态特征向量u,矩阵A和矩阵B可以表示为:

由式(11),得到:
(44)
式(44)的特征方程等价于:
(mλ2+3cλ+3k)(mλ2+cλ+k)=0
(45)
进一步,式(45)的特征值可以推导成如下的形式:
(46)
其中ξ=c/2mω,ω2=k/m。考虑到该二自由度振动系统的特征值是两对共轭复根,将c=1,k=9,m=1代入式(46)得到:
λ1,2=-0.5±2.958i,λ3,4=-1.5±4.975i
(47)
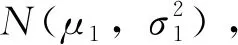
考虑式(39),由本节方法计算出的复特征值方差见表1。

表1 所提方法计算出的复特征值的方差
为了验证本文中所提出的方法,在本数值算例中,Monte-Carlo Simulation (MCS)被使用来计算复特征值的方差。此外,为了确定MCS方法中使用的样本容量,首先测试不同样本大小下MCS方法计算出的方差结果,见表2。
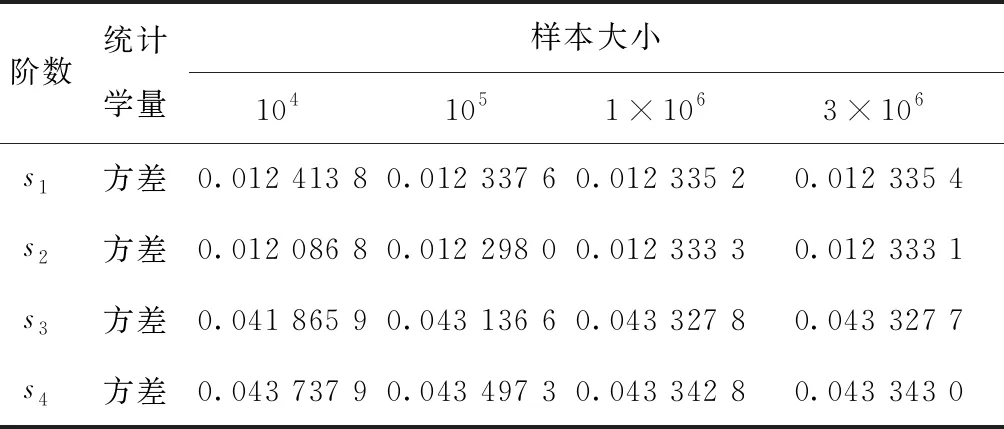
表2 确定MCS方法的样本容量
如表 2所示,随着样本容量的增大,MCS方法计算的结果趋于稳定。特别的,当样本容量大于1×106,由MCS方法计算出的复特征值的方差收敛。因此,在本算例中取MCS方法的样本容量为1×106是可信和合理的。进一步,由本文方法计算出的复特征值方差与由MCS方法计算出的复特征值方差对比见表3。

表3 由MCS方法和本文方法计算得到的复特征值方差的比较
注意到由本文方法计算得到的方差比MCS方法计算得到的要小。分析之后,主要有两个原因:第一,本文中所提出的方法是基于一阶矩阵摄动方法建立起来的,所以与精确解肯定会有一定的偏差,在采用二阶或者更高阶的矩阵摄动方法之后,这一偏差将会显著减小;第二,本文中的随机刚度矩阵Kr,随机阻尼矩阵Cr,随机质量矩阵Mr被假设为独立变量,亦即
在本方法中不考虑不同随机参数矩阵之间的相关性。也就是说,在本文方法的计算中只计及每一个随机参数矩阵自身的二次项,而不计及每一个随机参数矩阵的交叉项。这一求解策略同样导致由本方法计算得到的复特征值的方差相比MCS方法得到的结果要小。
多项式混沌展式(PCE)方法同样在本算例中被使用,来验证本节中所提出方法的可行性和准确性。根据本算例中不确定结构参数(m,c,k)的分布类型,选定Hermite多项式作为正交多项式基函数[7-9]。本算例中的随机变量的维数是三,Hermite多项式的最高阶次被分别设为1和2,以增强对比效果。由于使用Hermite多项式作为PCE方法中的正交基函数,如果Hermite多项式的最高阶次为p,则(p+1)次Hermite多项式的根一般被取做相应的配点。对于p=1,二阶Hermite多项式的根为ξ=±1,相应的配点分布如图
2所示,对应的PCE展式可以写成:
(48)

(49)
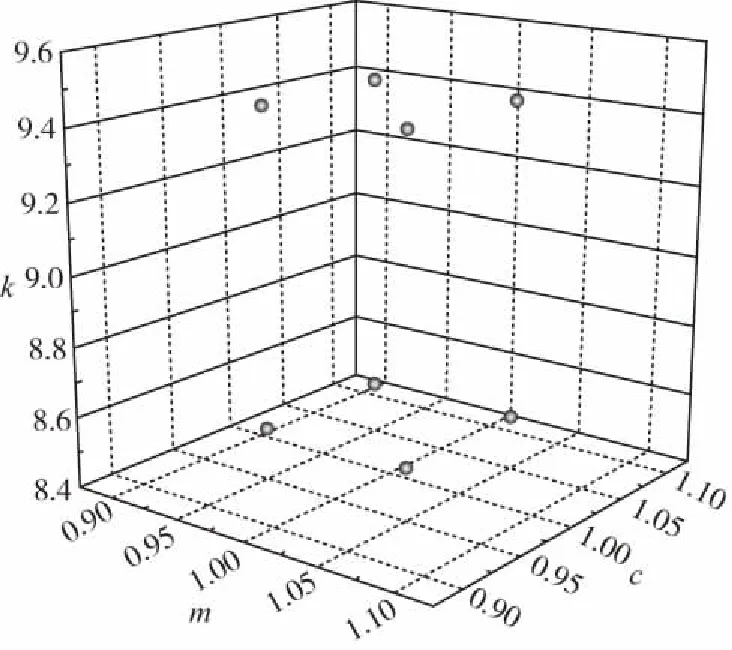
图2 p=1时PCE方法对应的配点分布
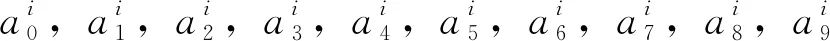
确定完变量空间的配点之后,利用基于最小二乘法的回归分析来求解上述Hermite多项式的待定系数。结合本算例中随机结构参数m,c,k的分布类型,得出了p=1和p=2时的复特征值λ1、λ2、λ3、λ4的多项式混沌展式见表4。进一步,基于多项式混沌展式,复特征值λ1、λ2、λ3、λ4的方差也能被直接求出,见表5。
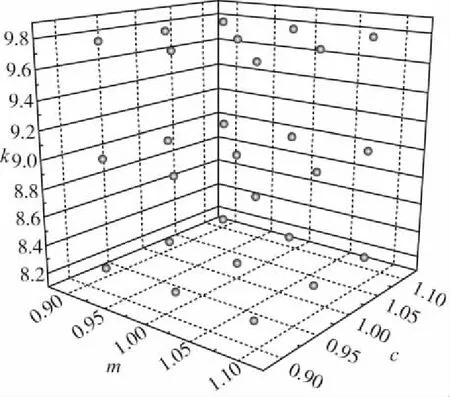
图3 p=2时PCE方法对应的配点分布

表4 算例一中的多项式混沌展式(变异系数=0.05)

续表4
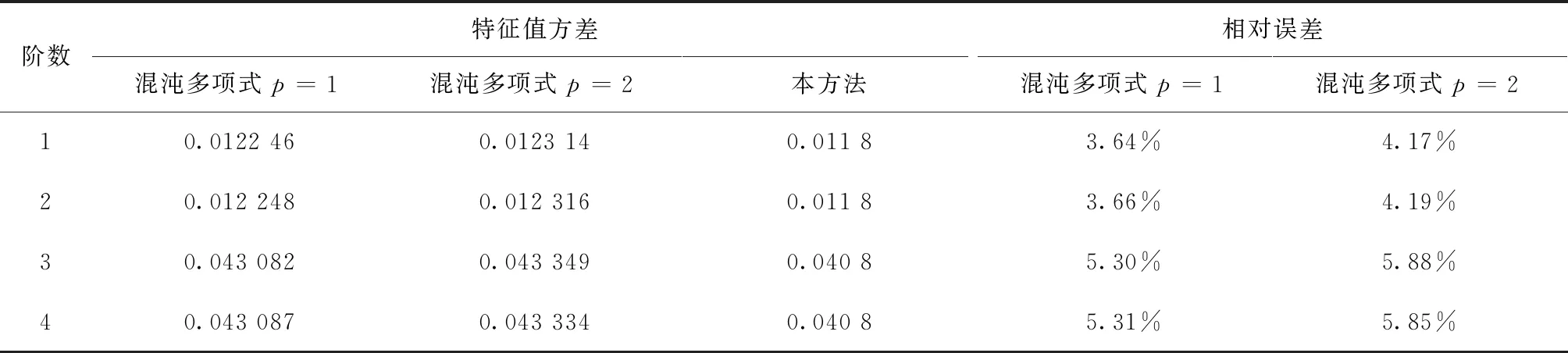
表5 本文方法和PCE方法计算复特征值方差的结果比较
在上述算例研究中,将随机结构参数的变异系数设定为一个固定的值(CV=0.05)。为了不失一般性,在以下的研究中,将考虑随机结构参数取不同大小的变异系数,来进一步研究本节方法的可行性和适用性。
对于本算例中所有的结构参数,不妨认为它们的变异系数同步从0.01变化到0.1。同时,注意到本数值算例中的特征值是成对出现的共轭复根。简明起见,以下只讨论Var(λ1)和Var(λ3),对于Var(λ2)和Var(λ4)来说,由于共轭复根的关系,很显然其结果与Var(λ1)和Var(λ3)是相似的。考虑随机结构参数取不同的变异系数,同时比较三种不同的不确定性分析方法(本节所提方法、MCS方法和PCE方法)所得的Var(λ1)和Var(λ3),其结果如图 4和图 5所示。
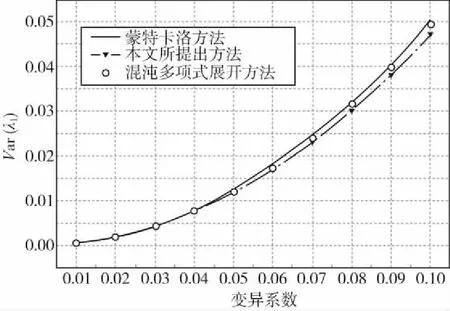
图4 不同变异系数下三种方法计算出的Var(λ1)结果比较

图5 不同变异系数下三种方法计算出的Var(λ3)结果比较
尽管变异系数在增加(从0.01到0.1),随机结构参数的不确定性在增大,但由本文提出方法计算出来的结果与MCS方法和PCE方法计算出的结果在总体趋势上保持一致。即使当变异系数增大到0.1时,本文方法计算出的结果与MCS方法和PCE方法之间的偏差仍然是可以接受的,这进一步验证了所提方法的可行性和适用性。另外,发现由本节方法计算得到的Var(λ1)和Var(λ3)相比MCS方法和PCE方法的结果偏小,这与表 3和表 5的结果对比一致,相关原因已经在上文中讨论过。
比较所提方法、PCE方法和MCS方法所需的计算时间,本文所提方法在计算效率方面具有明显的优势,如图6所示。
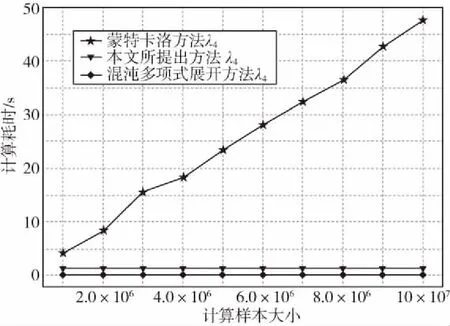
图6 三种方法的计算耗时比较
随着样本大小的增大,MCS方法的计算耗时显著增大。因此当处理某些大型复杂结构时,MCS方法的计算耗时将是无法承受的。对于PCE方法,尽管计算耗时相对于MCS方法已经减少很多,但是由于该方法需要在各个配点处进行计算,所以在计算耗时上相比于本文所提方法仍然大了几乎一个数量级。反观本文所提方法,其计算成本相对较低,这不仅提高了结构不确定性分析和结构重分析的计算效率,并且能够缩短具有复模态结构的设计优化周期。
为了更加直观地比较三种方法的计算耗时,形成图 6,这样本文方法在计算效率方面的优势被更直接和充分地展现。需要指出的是,本文所提出的方法、PCE方法和MCS方法都是在同一台Intel Core i7-2600@3.40GHz电脑上被执行的。
4.2 算例二:五自由度弹簧质量块系统
如图7所示,一个五自由度弹簧质量块力学系统被作为说明算例,来进一步验证本文所提出的方法。同时,假设振动只在竖直平面内发生。

图7 五自由度弹簧质量块系统
该系统中质量矩阵M的元素可以表示为:
(50)
其中Ji(i=4,5)表示惯性矩,L为正方形面板的边长,θi(i=4,5)表示转动角。
该系统中刚度矩阵K的各个元素可以写成:
(51)
而阻尼矩阵C的各元素为:
(52)
假设本算例中所有的结构不确定参数均满足高斯随机分布,同时有k3=k4=k5=k6=kG,c3=c4=c5=c6=cG。并且,令k1,k2和kG分别满足高斯分布N[15 000,(0.05×15 000)2],N[30 000,(0.05×30 000)2]和N[1 000,(0.05×1 000)2];令c1,c2和cG分别满足高斯分布N[6,(0.05×6)2],N(9,(0.05×9)2]和N[40,(0.05×40)2];令m1,m2,m3和L分别满足高斯分布N[300,(0.05×300)2],N[750,(0.05×750)2],N[1 500,(0.05×1 500)2]和N[1,(0.05×1)2]。
首先,将各个结构参数的均值取为它们的名义值,则该振动系统的名义参数矩阵可以表示如下:

(53)
进一步得到振动系统的名义复特征值如下(共5对共轭复根,其中有两对在数值上相同):
(54)
考虑各个结构参数的不确定性,根据本节所提出的计算方法,得到了该振动系统复特征值的方差(表6)。简明起见,每一对不同的共轭特征值中,仅仅取一个特征值进行计算。

表6 由MCS方法和本文方法计算得到的复特征值方差的比较 (变异系数=0.05)
如表6所示,这一部分的计算是将算例中所有10个不确定参数的变异系数均取为0.05。作为对比算法,经计算,本算例中蒙特卡洛方法的样本容量取为106。通过比较两种方法的计算结果及其相对误差发现,本节所提出方法的计算结果完全能够满足工程应用的要求。
在前面的讨论中,研究了在不确定结构参数取固定变异系数的情况下,本节所提出方法的计算精度。为了进一步研究所提出方法的计算能力和计算精度,在下面的讨论中,考虑不确定结构参数取变化的变异系数,同时假设所有的不确定结构参数的变异系数同步变化。简明起见,有针对性地取Var(λ1)进行研究,对于Var(λ3)、Var(λ5)和Var(λ7),其讨论过程是相似的。
图8比较了由所提出方法和MCS方法计算得到的复特征值的方差[i.e.Var(λ1)]。可以看出,随着变异系数的增大,由所提出方法计算得到的复特征值的方差也在逐渐增大;由MCS方法计算得到的结果与之具有相同的趋势,但在计算结果的数值上偏大一些。当不确定结构参数的变异系数取较小值时,两种方法所得结果非常接近,误差很小;当不确定结构参数的变异系数取值接近0.1时,两种方法计算结果的偏差逐渐增大。值得一提的是,当变异系数取0.1时,所提方法计算结果与MCS方法计算结果之间的相对误差仅为7.5%,在工程上依然是比较令人满意的。这也验证了本文所提方法的计算精度。
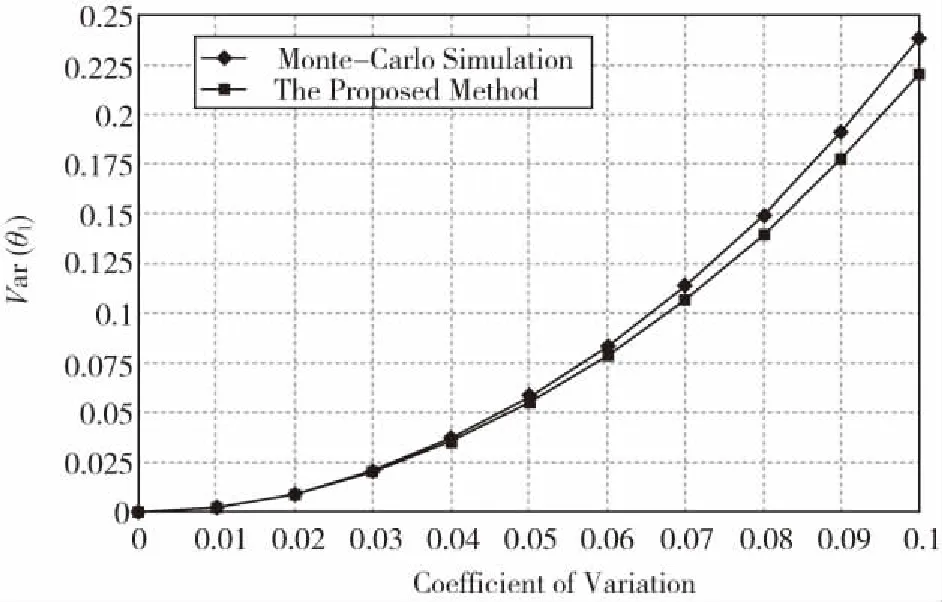
图8 由两种方法计算得到的Var(λ1)随变异系数的变化比较
通过对以上两个数值算例的分析和研究,对于具有随机结构参数的复模态结构系统,其不确定性传播分析的重要意义和必要性被充分地认识,结构参数的不确定性及其产生的影响也被深入地研究。不仅如此,数值算例表明,本文所提方法能够满足工程实际对于算法可行性和算法适用性的要求。
5 结论
本文将实模态结构随机摄动方法改进并推广到复模态特征值的不确定分析领域,改进的复模态随机摄动方法与概率理论相结合,建立了随机复特征值的方差关于随机结构参数的高效算法,开展了随机结构复特征值的不确定传播分析。
通过对多个数值算例的研究,本文所提出方法的可行性、适用性和计算精度得到验证。传统的矩阵摄动方法,为了进行结构特征值的不确定传播分析,需要预先假设或者通过大量的样本统计试验获得结构参数的相关系数矩阵,在工程上往往难以实现,所提出的改进的随机摄动方法不涉及结构参数的相关系数矩阵计算,因此克服了结构参数相关系数矩阵对于采用摄动方法进行随机特征值不确定性分析的制约。所提出的方法在工程上易于实现,并且使得计算随机结构特征值的统计学性质变得更为便利,为相应的动力学重分析和结构设计优化打下良好的基础。

