考虑成本和环境影响的RC梁可持续优化

章玉容，徐雅琴，袁伟斌，王龙龙

(1.浙江工业大学 土木工程学院，浙江 杭州 310023;2.杭州市商贸旅游集团有限公司 浙江 杭州 310003)

建筑业是一个典型的高消耗、高排放行业，面临着巨大的节能减排压力。建筑行业与环境问题密切相关，其能耗占全球总能耗的25%～40%[1]，二氧化碳排放量约占全球温室气体排放量的76%[2]。传统的土木工程结构优化往往以成本最小化、重量最小化和尺寸优化作为优化目标，例如，俞铭华等[3]对钢筋混凝土单筋梁进行成本优化来寻求最小成本下梁的截面尺寸和配筋率，王向[4]通过优化框架的尺寸和配筋，使得其成本降低14.22%。随着可持续意识的提高以及国家对节能减排的要求越来越严格，如何降低结构/构件的环境影响并提高其可持续性，已成为结构工程师亟需解决的问题之一。建筑行业是材料和能源消耗大户，通过结构优化设计，微小的材料用量降低就能较大幅度地减少建筑业的总环境影响。可持续优化设计旨在考虑结构/构件安全性能满足要求的前提下，寻求成本和环境影响最优的设计方案。Yeo等以成本和内含能(内含碳排放)为优化目标，对钢筋混凝土矩形梁[5]和钢筋混凝土框架[6]进行了结构设计优化，内含能(碳排放)最优方案比成本最优方案可减少5%～10%的环境影响。由此可知略微提高结构/构件的成本，可有效降低其能源消耗或碳排放。Paya等[7]通过模拟退火法对两跨四层的钢筋混凝土框架的成本、可施工性、整体安全和可持续性进行多目标优化，结果表明与成本最小方案相比，某一增量成本可接受的方案将具有更好的可施工性和安全性，且可持续性更佳。但是，上述研究成果在分析环境影响时仅考虑单一影响类别(能耗或碳排放)，可持续设计优化结果的科学性有待考证。众所周知，环境影响类别众多，不同类别环境影响的相对重要性不同，有必要在进行环境影响分析时选择合理的方法对各类环境影响评价指标进行归一化处理。

生命周期评价(Life cycle assessment, LCA)方法可量化衡量产品在原材料开采及产品制造、产品的使用和维护，以及最终的处理等生命周期各个阶段的环境负荷，其技术框架包含以下四个方面：目标与范围确定、清单分析、环境影响评价和结果解释[8]。目前国际上关于环境影响评价还没有统一的方法，一般可采用中点模型和终点模型两种方法进行环境影响评价。终点模型因其可将环境影响追踪量化到影响链的末端进行评价，有利于解释环境问题的客观本质和最终损伤，成为国际研究热点[9]。GaBi软件由于其强大的功能、人性化的界面和模拟分析等优点，已成为LCA分析应用最为广泛的工具之一[10]。因此，本研究采用GaBi软件中内嵌的终点模型——ReCiPe 2008，结合优化设计方法，以环境影响和成本为目标函数构建了钢筋混凝土梁的可持续设计优化模型，确定其在满足《混凝土结构设计规范》(GB 50010—2010)[11]要求前提下的成本最优方案和环境影响最优方案，并通过分析两种最优方案的成本差异和环境影响差异来得到可持续优化的目的。与此同时，针对满足设计规范的每一种RC梁的可行方案，分析了RC梁总成本和总环境影响随截面宽度和高度的变化规律。最后，研究了混凝土和钢筋的的单位成本和单位环境影响波动对RC梁最优截面尺寸、配筋率和可持续优化效果的影响。

1 梁的可持续优化设计方法

本研究以钢筋混凝土梁的环境影响和成本为目标函数，根据混凝土结构设计规范确定设计变量的约束条件，建立钢筋混凝土梁的可持续设计优化模型。

优化设计的设计变量应能描述RC梁的性能和形状。RC梁的设计变量为梁宽b、梁高h、混凝土强度fc、梁的纵向受拉钢筋总面积As，纵向钢筋的总面积由钢筋数量n和直径d来确定。考虑实际工程情况和中国混凝土结构设计规范的要求，梁的截面尺寸和纵向钢筋尺寸需要满足特定的模数，故上述5 个变量均为离散变量。

以单位长度梁的成本和环境影响为目标函数，计算方法为

(1)

(2)

式中：C和E分别为单位长度梁的成本和环境影响；ρs为钢筋的密度，取值为7 850 kg/m3；Cc和Cs分别为混凝土和钢筋的单位成本，其值根据浙江信息造价网确定(表1)；Ec和Es为生产混凝土和钢筋的单位环境影响，可通过GaBi软件中内嵌的终点模型——ReCiPe 2008建模分析确定，具体的分析过程如图1所示。

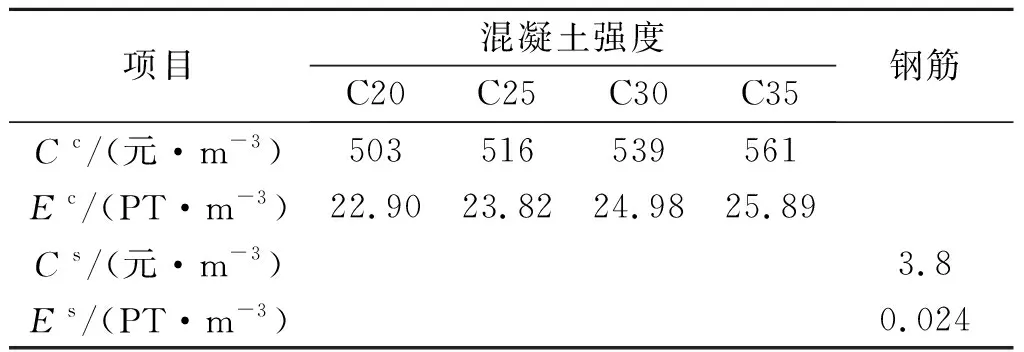
表1 混凝土和钢筋的成本和环境影响

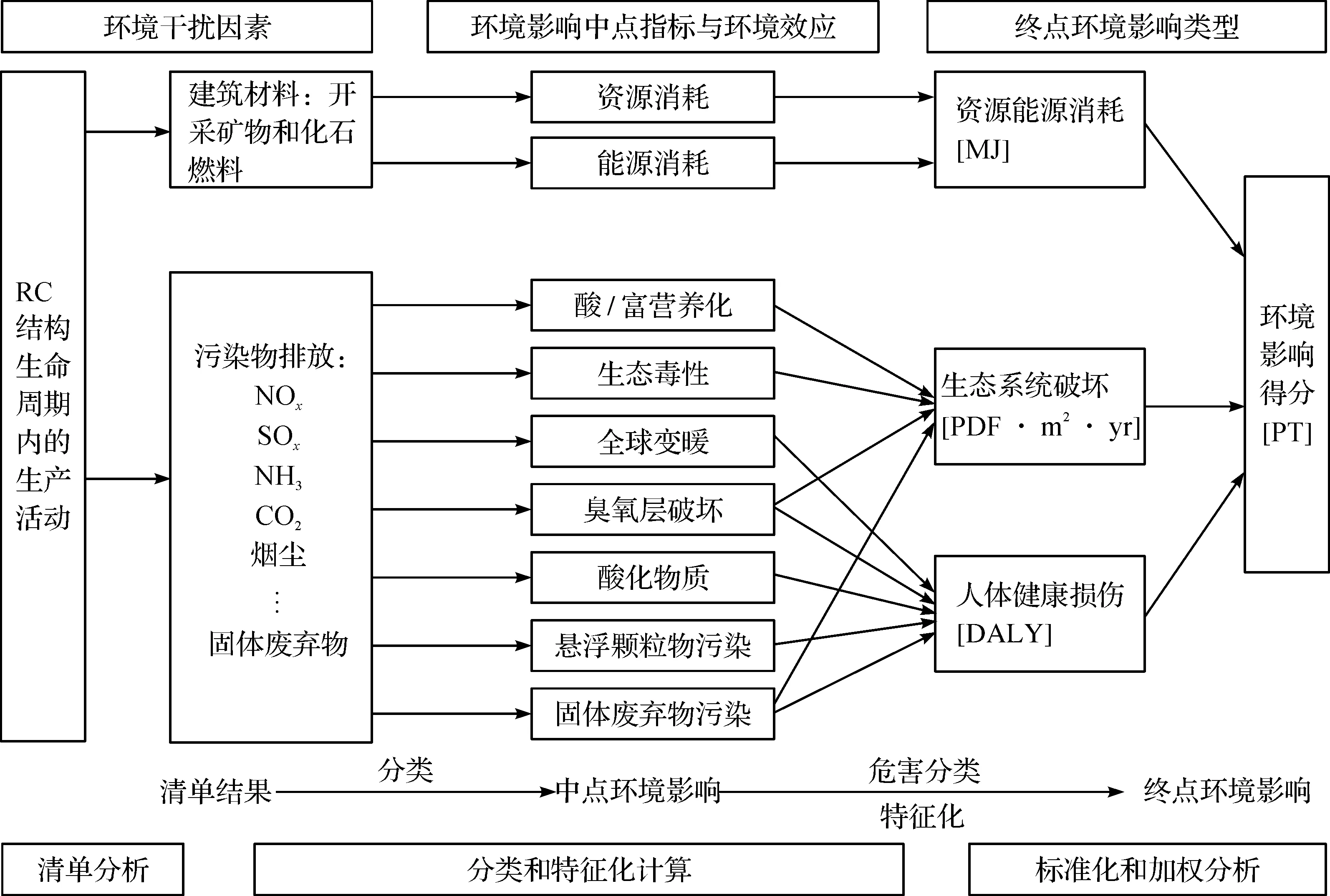
图1 LCA终点模型的环境影响分析过程 (ReCiPe 2008方法)Fig.1 Environmental impact analytical process of end-point LCA (ReCiPe 2008)

由图1可以看出：ReCiPe 2008方法可对环境影响评价的特征化评价结果标准化，将不同类型的环境影响值统一为无量纲值，并以环境影响得分(PT)衡量。采用GaBi软件可建模得到混凝土和钢筋的单位环境影响，考虑到钢筋的可回收性，一般回收率为90%[12]，故应对钢筋的环境影响进行折减，最终单位环境影响如表1所示。

根据混凝土结构设计规范，钢筋混凝土梁的约束条件有：

1) 正截面受弯承载力约束条件为

(3)

(4)

式中：Mu为正截面受弯承载力设计值；M为弯矩设计值；fc为混凝土抗压强度设计值；x为梁截面混凝土受压区高度；h0为梁截面有效高度，h0=h-as；as为纵向受拉钢筋合力点到混凝土截面受拉边缘的距离，取为40 mm；fy为纵向钢筋的抗拉强度设计值；α1为等效矩形应力图系数，当混凝土强度不大于C50时，取值为1；ξb为界限相对受压区高度。

2) 斜截面抗剪承载力约束条件为

(5)

式中：Vu为构件斜截面上混凝土和箍筋的受剪承载力设计值；V为剪力设计值；ft为混凝土抗拉强度设计值；fyv为箍筋的抗拉强度设计值；Asv为配置在同一截面内箍筋各肢的全部截面面积；s为沿构件长度方向的箍筋间距。

3) 尺寸约束条件为

0.25βcfcbh0≥V

(6)

h/b=2～3.5

(7)

式中βc为混凝土强度影响系数，当混凝土强度不超过C50时，取为1。

4) 配筋率约束条件为

(8)

(9)

式中：ρ为纵向受拉钢筋的配筋率；ρsv为箍筋配筋率。

通过对梁的每个设计变量进行约束计算，可确定符合规范要求的设计变量，并得出梁设计方案的可行域。可行域定义为符合所有设计规范的部分可行设计变量，而不可行的变量对应不满足一个或多个约束条件，通过对可行域进行优化分析来实现梁的可持续性设计。

2 实例分析

以某一钢筋混凝土(RC)矩形简支梁为例来确定其成本/环境影响最优的设计方案，并考虑各个设计变量改变对目标函数的影响，由此来评估RC梁的可持续优化设计潜力。梁跨度6 m，受均布荷载作用，跨中弯矩为225 kN·m，两端剪力为150 kN。梁的宽度和高度范围分别为250～400 mm和500～800 mm，并以50 mm为模数；梁的受拉钢筋最多为两层布置且对称布置，钢筋数量取2～6 根；钢筋尺寸范围为8，10，12，14，16，18，20 mm；梁的纵筋使用HRB400级钢筋；混凝土强度等级为：C20，C25，C30，C35；梁的箍筋为HPB300，箍筋间距设为s=150 mm，直径为8 mm；当梁的腹板高度为450～650 mm时，在梁的两侧沿高度配置4 根直径为12 mm的HRB400纵向构造钢筋；当梁的腹板高度为650～800 mm时，在梁的两侧沿高度配置6 根直径为12 mm的HRB400纵向构造钢筋。由上述梁的设计变量，可确定出6 860 种RC梁的设计方案。所选定的设计变量均为离散变量，符合实际工程概况。本研究采用MATLAB软件对RC梁所有的设计方案进行编程，可输出由设计变量组合成的每一种可行的设计方案，故此种计算方法更便于观察目标函数随设计变量变化的趋势，并避免了其他优化程序计算得到的并不是全局最优解的缺点。

根据约束条件确定梁设计方案的可行域，并通过式(1，2)计算出RC梁每种设计方案的总成本和总环境影响。以混凝土强度等级C30为例，图2给出了总成本/总环境影响随截面高度和宽度的变化规律。由图2可知：对于矩形梁不同的截面尺寸，单位长度的RC梁的总成本在130～250 元之间，总环境影响在3～8 PT之间；总成本和总环境影响随截面尺寸的变化并无一致规律，即计算得到的梁的成本最优设计方案的尺寸并不对应环境影响最优设计方案的尺寸。

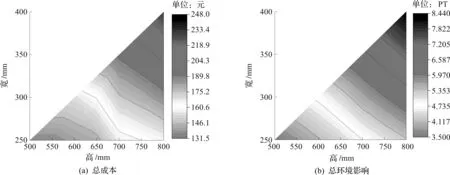
图2 RC梁设计的可行域(C30)Fig.2 Feasible designs of RC beam(C30)

为分析混凝土和钢筋对RC梁总成本和总环境影响的贡献，图3给出了不同可行设计方案中混凝土和钢筋在总成本和总环境影响中的占比。由图3可知：混凝土成本占总成本的49%～78%，而混凝土对总环境影响贡献在87%以上；钢筋对总环境影响占比最高为12%左右，小于钢筋对总成本的贡献(22%～51%)。由此可知，混凝土对总环境影响的贡献大于对总成本的贡献，钢筋则相反。因此，降低混凝土用量可降低混凝土结构环境影响，从而提高其可持续性。

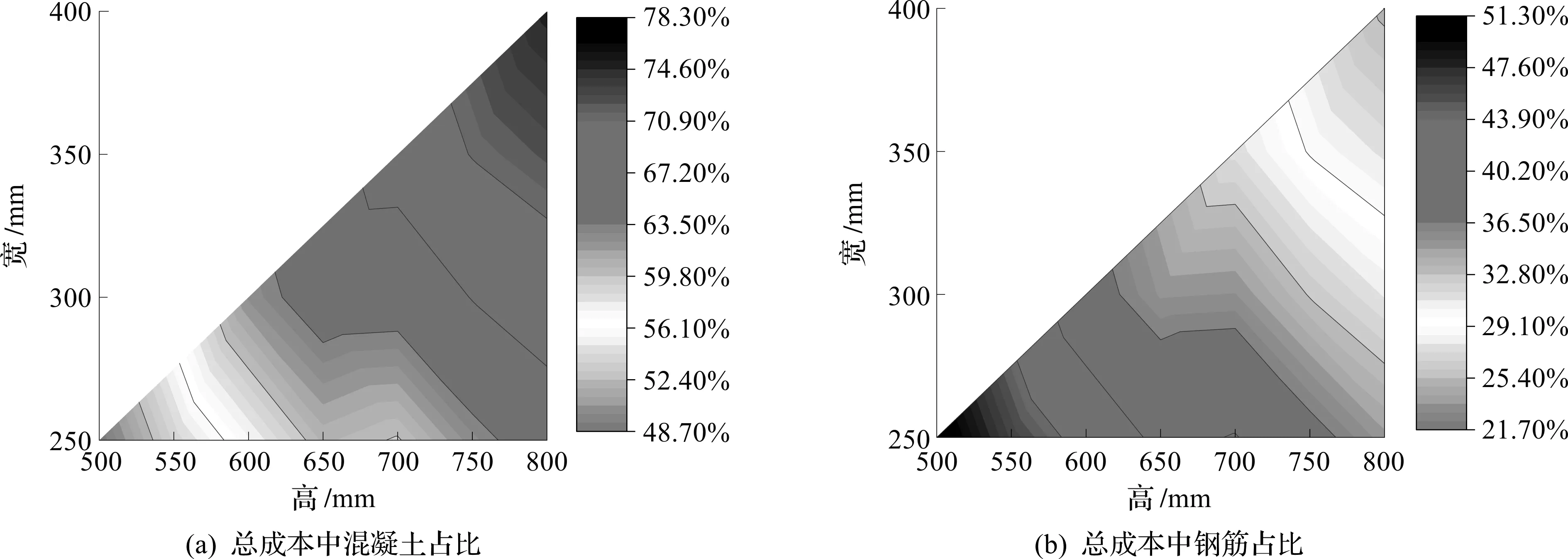
图3 混凝土和钢筋占总成本和总环境影响比例Fig.3 Ratio of concrete and reinforcement to total economic cost and total environmental effects

图4给出了RC梁总成本和总环境影响随截面尺寸的变化规律。从图4可以看出：RC梁总成本随着高度逐渐增加，而RC梁的总环境影响随着高度的增加呈现快速上升的趋势。上述结果表明：截面高度的增加会加大混凝土用量而降低钢筋用量，当减少的钢筋成本低于增加的混凝土成本时，表现为RC梁总成本随截面高度降低，反之则表现为RC梁总成本随截面高度升高而升高。但是，钢筋对总环境的贡献远小于混凝土对总环境影响的贡献，钢筋用量的下降导致的环境影响降低量无法抵消由于混凝土用量增加导致的环境影响增加量。由此可见，优化截面高度可有效降低RC梁的环境影响，但在降低RC梁的成本上效果甚微。

图4 成本/环境影响与RC梁截面尺寸的关系(C30)Fig.4 Relationship between cost/environmental impact and section size of RC beam(C30)

3 优化结果分析

根据可行域和目标函数，计算得到每种混凝土强度等级下RC梁的成本最优方案和环境影响最优方案，如表2所示。

表2 不同混凝土强度等级下成本与环境影响最优方案

由表2可知：混凝土强度等级对RC梁的环境影响最优方案的截面尺寸的影响和对成本最优方案的截面影响一致。总体上混凝土强度等级的提高可降低RC梁成本最优方案和环境影响最优的截面尺寸。

在相同混凝土强度等级下，RC梁成本最优方案截面均大于环境影响最优方案的截面，且RC梁成本最优方案所需钢筋用量均小于环境影响最优方案的截面。以C30为例，RC梁的成本最优方案的截面为250 mm×600 mm，而环境影响最优方案的截面为250 mm×500 mm，这是因为降低混凝土的高度可有效降低环境影响所导致的；RC梁的成本最优方案的截面配筋率为0.909%，环境成本最优方案的截面配筋率为1.634%，根据混凝土设计规范，单筋矩形梁的经济配筋率约为0.6%～1.5%，故环境影响最优方案的配筋率也在合理范围之内。由此可见：RC梁成本最优方案的截面相对于环境影响最优方案的截面，具有更多的混凝土用量和更少的钢筋用量。

为了分析RC梁环境成本最优方案和成本最优方案的成本差异和环境影响差异。本研究将RC梁环境最优化方案的成本(Cenviromental-optimized)与成本最优方案的成本(Ccost-optimized)比值定义为Rcost；成本最优方案的环境影响(Ecost-optimized)与环境影响最优方案的环境影响(Eenviromental-optimized)比值定义为Re。Rcost和Re的表达式分别为

(10)

(11)

RC梁成本优化方案和环境影响优化方案之间的成本差异和环境影响差异随混凝土强度等级的变化如表2所示。当混凝土强度等级为C30时，RC梁环境影响最优方案相对于成本最优方案，环境影响降低了15%左右，成本增加不到4%。在实际工程中，在可以接受成本增加的前提下，可适当提高钢筋混凝土结构的成本来有效地降低其环境影响，从而在经济性和环境影响之间进行权衡。当混凝土强度提高时，RC梁的两种优化方案的成本差异有微小提高，而环境影响差异显著提高。因此，提高RC梁的混凝土强度等级，可以提高环境影响优化效果，即较少的成本增加，导致较多的环境影响的降低。

为识别出影响RC梁成本最优方案/环境影响最优方案的主要影响因素，对混凝土的成本Cc、混凝土的环境影响Ec、钢筋的成本Cs和钢筋的环境影响Es这4 个评价指标进行敏感性分析，找出影响成本最优方案/环境影响最优方案的最敏感因素，并利用敏感系数β来反映其对目标函数的影响程度，即

(12)

不确定因素变动百分比选10%，分析上述4 个评价指标的波动为10%时对成本和环境影响最优方案的敏感性，计算结果如表3所示。

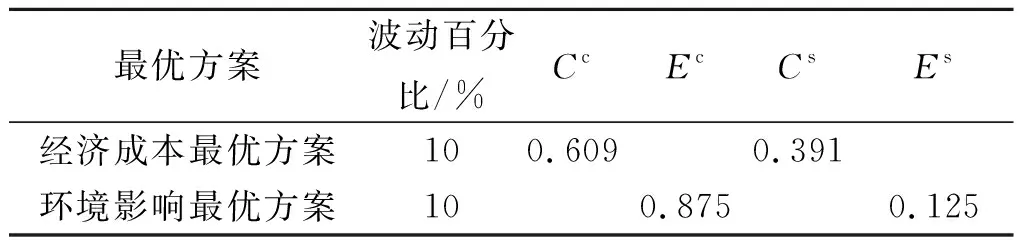
表3 成本和环境影响最优方案的敏感系数

由表3可知：对于成本最优方案，混凝土成本对总成本的影响要大于钢筋成本对总成本的影响；对于环境影响最优方案，混凝土环境影响对RC梁成本最优方案的总环境影响更为敏感。

4 Rcc，Rcs，Rec和Res对优化设计的影响

为分析混凝土和钢筋的成本和环境影响变化对RC梁的环境成本最优方案和成本最优方案的截面尺寸、配筋率、环境差异和成本差异的影响，本研究提出了4 个指标：混凝土和钢筋的成本波动率(Rcc和Rcs)，混凝土和钢筋的环境影响波动率(Rec和Res)。根据相关文献，设定混凝土和钢筋的成本波动率范围为0.5～1.5倍[4,13-16]。

4.1 最优截面面积和最优配筋率与Rcc，Rcs，Rec和Res的联系

为了分析Rcc，Rcs，Rec和Res对RC梁的成本最优方案和环境成本最优方案的截面面积和配筋率的影响，以混凝土等级为C30的RC梁为例，混凝土和钢筋成本和环境影响的基准值如表1所示，即Cc为539 元/m3，Cs为3.8 元/kg，Ec为24.98 PT/m3，Es为0.024 PT/kg，钢筋和混凝土成本和环境影响波动对RC梁可持续优化设计的影响如图5所示。波动率大于1表示单位成本/环境影响大于本文设定值，波动率小于1表示单位成本/环境影响小于本文设定值。

图5 Rcc，Rcs，Rec和Res对最优方案截面面积和配筋率的影响(C30)Fig.5 Effects of Rcc，Rcs，Recand Res on sections area and reinforcement ratio of optimal solutions (C30)

由图5可知：当Rcc，Rcs，Rec和Res分别为1时，RC梁成本最优方案的截面面积和配筋率分别为0.15 m2和0.90%；RC梁的环境影响最优方案的截面面积和配筋率分别为0.125 m2和1.63%。不论Rcc，Rcs，Rec和Res如何变化，RC梁成本最优方案的截面面积均大于环境影响最优方案的截面面积，环境影响最优方案的配筋率均大于成本最优方案的配筋率。Rec和Res的变化对RC梁的成本和环境影响最优方案的截面面积和配筋率并无影响，成本(环境影响)最优方案的截面面积和配筋率均为0.15 m2(0.125 m2)和0.91%(1.63%)。当Rcc和Rcs变化时，RC梁的环境影响最优方案的截面面积和配筋率保持不变，均为0.125 m2和1.63%，但成本最优方案的截面面积和配筋率有显著变化。当Rcc大于1时，成本最优方案的截面面积减少至0.138 m2，且仍大于环境影响最优方案的截面面积；成本最优方案的配筋率增大至1.20%，且仍小于环境影响最优方案的配筋率；当Rcc小于1时，RC梁的成本最优方案的截面面积和配筋率不随Rcc改变。当Rcs大于1时，成本最优方案的截面面积和配筋率保持不变；当Rcs小于1时，成本最优方案的截面面积减小至0.138 m2，而配筋率增大至1.2%。

4.2 Rcost和Re与Rcc，Rcs，Rec和Res的联系

以混凝土等级为C30为例，分析Rcc，Rcs，Rec和Res对RC梁成本最优方案和环境影响最优方案的成本差异和环境影响差异的影响。图6(a～d)分别表示RC梁成本优化方案与环境影响优化方案之间的成本差异Rcost和环境影响差异Re与Rcc，Rcs，Rec和Res的联系。

图6 Rcc，Rcs，Rec和Res与Rcost和Re的联系(C30)Fig.6 Relationships of Rcc，Rcs，Rec，Res and Rcost，Re (C30)

由图6可知：当Rcc，Rcs，Rec和Res均为1时，RC梁环境影响最优方案相对于成本最优方案，环境影响减少了15%左右，成本增加不到4%。此外，由图6(a)可知：Rcc大于1时，Rcost随Rcc逐渐减小，而Re随Rcc先减少后趋于平缓；当Rcc小于1时，Rcost随Rcc降低逐渐增大，而Re随Rcc降低保持不变，故在其他因素保持不变的前提下，Rcc变大有利于RC梁的可持续优化设计。由图6(b)可知：当Rcs大于1时，Rcost随Rcs逐渐增大，Re随Rcs保持不变；当Rcs小于1时，Rcost随Rcs逐渐减小，Re与也随Rcs逐渐减小，故在其他因素保持不变的前提下，Rcs减小有利于RC梁的可持续优化设计。由图6(c)可知：当Rec大于1时，Rcost随Rec保持不变，Re随Rec逐渐增大；当Rec小于1时，Rcost随Rec保持不变，Re随Rec逐渐减小，故在其他因素保持不变的前提下，Rec变大有利于提高RC梁可持续优化设计。由图6(d)可知：当Res大于1时，Rcost随Res保持不变，Re随Res逐渐减小，当Res小于1时，Rcost随Res保持不变，Re随Res逐渐增大，故在其他因素保持不变的前提下，Res减小有利于RC梁的可持续优化设计。

由图6还可知：随着Rcc，Rcs，Rec和Res变化，环境影响最优方案可使RC梁的环境影响降低约8%～18%，同时，环境影响优化方案的成本要比成本优化方案的成本高大约1%～10%。由此可见，环境影响的精确减少在很大程度上取决于Rcc，Rcs，Rec和Res的变化。

4 结 论

本研究以钢筋混凝土梁的环境影响和成本为目标函数，构建了钢筋混凝土梁的可持续设计优化模型，以RC梁为例进行案例分析，主要结论如下：

1) RC梁的成本和环境影响随截面尺寸的变化并无一致规律，即环境影响最优截面不一定对应成本最小截面。混凝土对RC梁总环境贡献大于混凝土对RC梁的总成本贡献，钢筋则相反。优化RC梁的截面宽度，可同时降低总成本和总环境影响；优化截面高度，可有效降低总环境影响。

2) 针对本文案例，RC梁环境影响最优方案相对于成本最优方案，环境影响降低了15%左右，成本增加不到4%。提高RC梁的混凝土强度等级，较小的成本增加即可显著降低环境影响；敏感性分析结果表明混凝土的单位成本和环境影响对RC梁的优化结果影响最大。

3) 混凝土和钢筋单位成本及环境影响的波动对RC梁成本最优方案和环境影响最优方案的截面面积、配筋率和优化效果具有一定的影响。混凝土的单位成本和单位环境影响增大，钢筋的单位成本和单位环境影响减小有利于RC梁的可持续优化设计。环境影响的精确减少在很大程度上取决于钢筋与混凝土的单位成本与单位环境影响的变化。