基于PSO 优化与深度信念网络的机炉协调系统建模研究

吴林峰，孟瑜炜，俞荣栋，张震伟，徐仙华，王 豆，郭 鼎

（1.浙江浙能技术研究院有限公司，杭州 311121；2.浙江浙能乐清发电有限责任公司，浙江 乐清 325600）

0 引言

机炉协调控制系统是火力发电厂自动控制生产系统的重要组成部分，表现出非线性、强耦合的特点[1-2]。随着风、光、水等可再生能源的快速发展，电网对燃煤机组运行的灵活性提出了更高要求。因此，建立一个具有自适应、准确的机炉协调系统模型对于提高机组整体性能，实现机组在复杂工况下保持最优控制具有重要意义。

目前在机炉协调系统建模问题上，主要有机理建模[3]、人工智能技术等方法。在机理建模方面，国际上具有代表性的BELL-Äström 模型[4]，建立了一个三输入三输出的非线性微分模型，为机炉协调系统的深入研究奠定了基础。在人工智能技术上，基于数据驱动的“黑箱建模”方法得到了广泛关注，支持向量机、神经网络[5-6]等机器学习已广泛应用于建模工作，但是支持向量机不同核函数的选择和构建对于模型辨识效果影响很大，并且难以处理大样本数据。神经网络可以处理多维样本数据，但是神经网络的结构和参数初始值通过经验法人为设定，模型会出现过拟合现象，训练过程容易陷入局部最优解。DBN（深度信念网络）克服了传统神经网络的局限性，具有自学习特征和数据降维的优势，目前在图像分类、故障诊断、回归预测[7-12]等领域取得了突破性进展。

本文首先对机炉协调系统模型的机理特性进行研究，建立三输入三输出的“黑箱子”数据驱动结构模型，然后利用DBN 算法处理输入数据，采用无监督贪婪逐层训练法初始化网络权值阈值，引入粒子群优化算法对RBM（受限玻尔兹曼机）隐含层节点数进行全局迭代寻优，最后结合BP（神经）网络在输出层构建联想记忆层实现回归分析功能。

1 单元机组协调系统模型

本文研究对象为超临界机组直流炉的协调系统。直流炉与汽包炉相比最大的不同是其给水经加热蒸发变成过热蒸汽的过程是一次性完成的，汽水之间没有明确的分界点，汽水流程由燃料与给水比值控制。当发生负荷需求时，迅速调节汽轮机调门，同时改变锅炉燃料量和给水量，可以快速响应汽轮机的蒸汽流量需求，进而响应机组负荷变化，实现外部能量平衡。而内部汽水平衡可以通过分离器出口中间点温度进行有效控制。

在某个固定负荷点，直流炉超临界机组协调系统模型的传递函数可由如下表达式描述[3]：

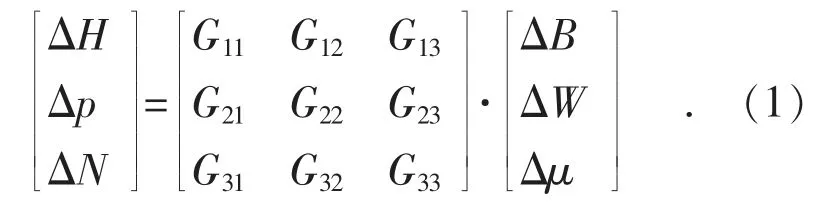
以上数学模型为三输入三输出的简化模型。其中，ΔB，ΔW，Δμ 是协调系统的输入控制量，分别为燃料量、给水量、汽机调门开度；ΔH，Δp，ΔN 是协调系统的输出控制量，分别为中间点焓值、主蒸汽压力、机组负荷。

额定条件下直流锅炉超临界机组协调系统模型的数学表达式如下：

式中：a1，a2，b1，b2，b3均为传递函数系数。

在实际的控制中，以上数学模型在求解过程比较复杂，一般需要经过等效变换进行简化控制。

因此，基于以上分析，对于超临界直流炉协调系统可以采用三输入三输出的“黑箱子”模型结构，如图1 所示。输入量为给煤量、给水量、汽轮机调门开度，输出量为机组负荷、主蒸汽压力、中间点温度。

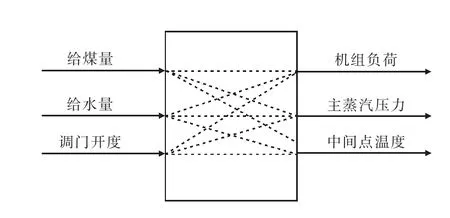
图1 协调系统模型结构

2 深度信念网络算法

DBN 是由Hinton 等人在2006 年提出的一种新的机器学习算法，是一个概率生产模型，由多个堆叠的RBM 和单层分类器构成的一种深度神经网络[13-14]，采用无监督贪婪逐层法预训练生成初始的权值阈值空间分布，具有强大的非线性能力。

一个典型的RBM 可视层和隐含层组成，如图2 所示。可视层与隐含层之间的神经元互相连接，而层内的神经元彼此独立。

图2 RBM 结构

RBM 是基于能量模型概念，可见层神经元与隐含层神经元的联合能量函数为：

式中：θ={ai，bj，wij}；ai是可视层神经元的偏置；bj是隐含层神经元的偏置；wij是可视层与隐含层连接权值。

根据能量函数，可以得到可见层和隐含层神经元的联合概率：

已知可视层神经元状态，隐含层神经元状态满足条件独立，则隐含层第j 个神经元状态激活的概率是：

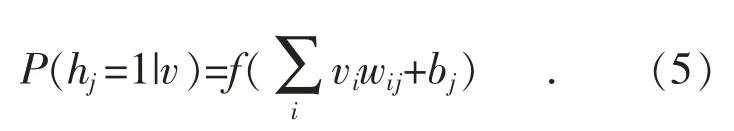
同理，已知隐含层神经元状态，则第i 个可视层神经元状态激活概率是：

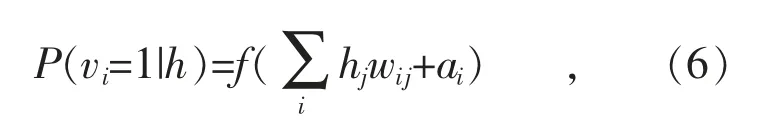
式中：f（x）=1/（1+e-x）。

RBM 训练采用对比散度法，根据数据特征重构输入样本，并与原始样本对比，以最大似然函数为目标调整参数θ，θ 可以通过对数似然函数求得：

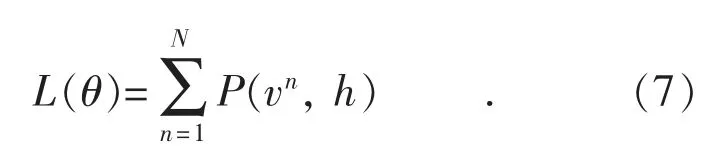
DBN 结构如图3 所示，由多个RBM 构成，最顶层为BP 神经网络。DBN 训练过程分为两步，预训练和微调。首先，采用无监督逐层预训练法自底向上对每一层RBM 进行预训练，上一层RBM 的输出作为下一层RBM 的输入，使得每一层都能学习到上一层的特征，获得初始权值。最后，利用顶层的BP 网络自顶向下有监督学习对网络进行反向微调，进一步优化网络参数。

3 粒子群优化算法

PSO（粒子群优化算法）是在对鸟类捕食行为研究的基础上发展而来的寻优算法[15-16]。首先，随机初始化一个粒子群，每个粒子都可能是解空间的最优解，计算每个粒子的适应度函数值，通过比较与极值点的适应度值，更新粒子属性，推动粒子朝着个体最优值和群体最优值方向迭代，直到全局最优。

图3 DBN 结构

粒子的迭代通过速度和位置来实现，迭代公式如下：

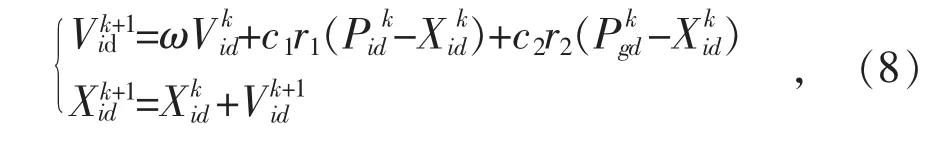
式中：ω 为惯性权重；c1，c2为加速因子；r1，r2为0 到1 之间的随机数；分别为第k次迭代中参数i 第d 维变量的速度、位置、个体极值最优解和群体极值最优解。

针对DBN 的结构特点，由多个RBM 层组成，RBM 隐含层节点数量的不同对网络的训练速度和精度影响很大，为此，引入PSO 优化算法，对DBN 结构中每一层RBM 隐含层的神经元数量进行全局寻优，训练过程中把DBN 输出的均方误差作为改进PSO 的适度函数，其计算公式如下：

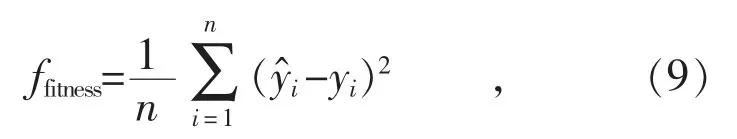
当适应度值达到预设误差要求或迭代次数时结束寻优，把当前的隐层神经元参数作为DBN的网络结构参数，最后利用优化后的DBN 对测试样本数据进行测试。

4 协调系统建模试验

选择某660 MW 超临界直流炉对机炉协调系统进行建模试验。根据机炉系统简化模型，采用三输入三输出“黑箱子”数据驱动建模法，采集给水量、给煤量、汽轮机调门开度、机组负荷、主蒸汽压力和中间点温度共6 个参数，采集时间间隔为5 s，共采集到16 000 组实时生产数据。

训练之前对数据进行预处理，采用数据抽取和滑动平滑的方法对原始数据进行消噪处理，减少异常值对模型的干扰。然后对数据进行归一化处理，将所有数据压缩在0～1，有助于加快模型的计算速度。归一化公式如下：

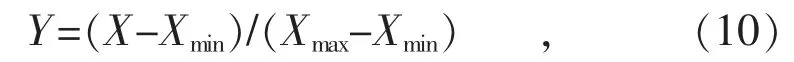
式中：X 和Y 分别为转换前后的值；Xmin和Xmax分别为样本数据的最小值与最大值。

预处理中数据抽取窗口设置为3，即每隔3组抽1 组，得到5 760 组数据，选择5 700 组数据进行建模和测试训练，其中前5 600 组作为模型训练数据，后100 组作为模型测试数据。

构建PSO-DBN 模型，设计一个4 层DBN 模型，RBM1—RBM4 的隐含层神经元数量取值范围为0～100，RBM 预训练次数100，每次训练数据分成50 团。采用PSO 算法对隐层数量进行寻优，粒子群算法初始参数设置为：ωmax=0.9，ωmin=0.5，cmax=0.9，cmin=0.5，种群规模20，迭代次数100。输入训练数据开始寻优。

经过100 次迭代得到各RBM 的最优的节点数，RBM1 取55 个、RBM2 取53 个、RBM3 取70个、RBM4 取38 个。根据寻优参数设置好DBN 网络参数，在有监督学习过程中采用BP 网络进行训练实现数据回归功能，BP 隐患层节点10 个，学习率0.1，输出层激活函数设置sigmoid 函数。

训练阶段模型的模型输出与实际值对比如图4—6 所示。从图中可以看到，训练阶段的PSODBN 模型能够很好地跟踪实际值，整体变化趋势与实际发展趋势一致，表明该模型具有良好的非线性拟合能力。

模型训练好之后，选择测试数据对该模型进行验证，输入100 组测试数据，模型计算后得到测试结果，如图7—9 所示。

图7—9 是PSO-DBN 机组协调系统模型的测试输出，由图中可以清晰地看到，机组负荷、主蒸汽压力和中间点温度的输出与实际值相近，并随着机组运行工况的变化而变化，总体发展趋势与实际值的发展趋势一致。

图4 训练阶段机组负荷预测值与实际值对比

图5 训练阶段主蒸汽压力预测值与实际值对比

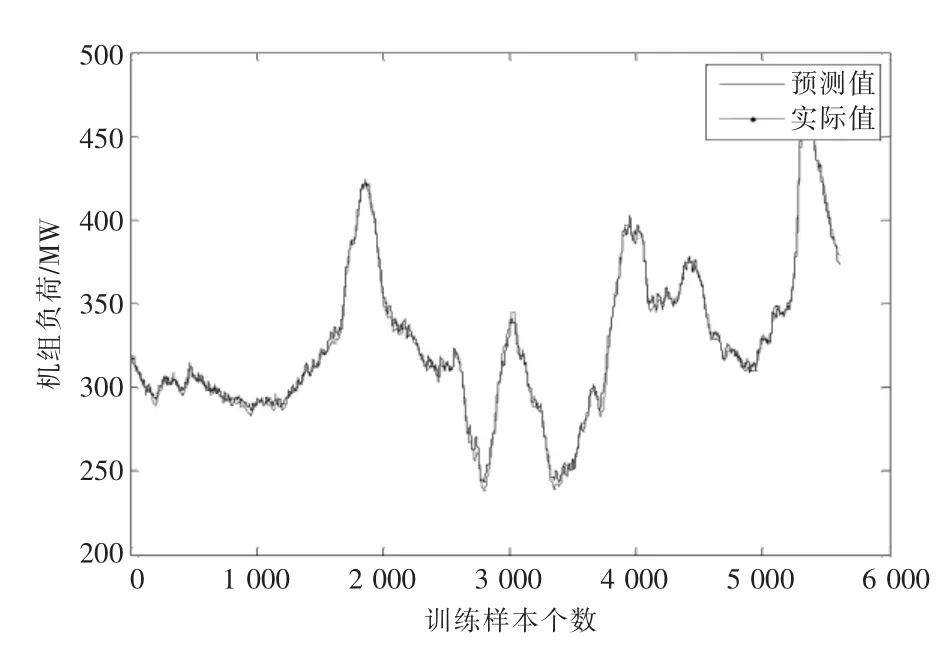
图6 训练阶段中间点温度预测值与实际值对比

随后对模型进行定量分析，分别计算绝对误差δMAPE、决定系数R2、相关系数C 等3 个评价指标，通过数据来说明模型的预测性能和拟合效果。为了分析对比，同时建立单独的DBN 预测模型与PSO-DBN 模型对比预测性能。

绝对误差δMAPE定义如下：

图7 测试阶段机组负荷预测值与实际值对比

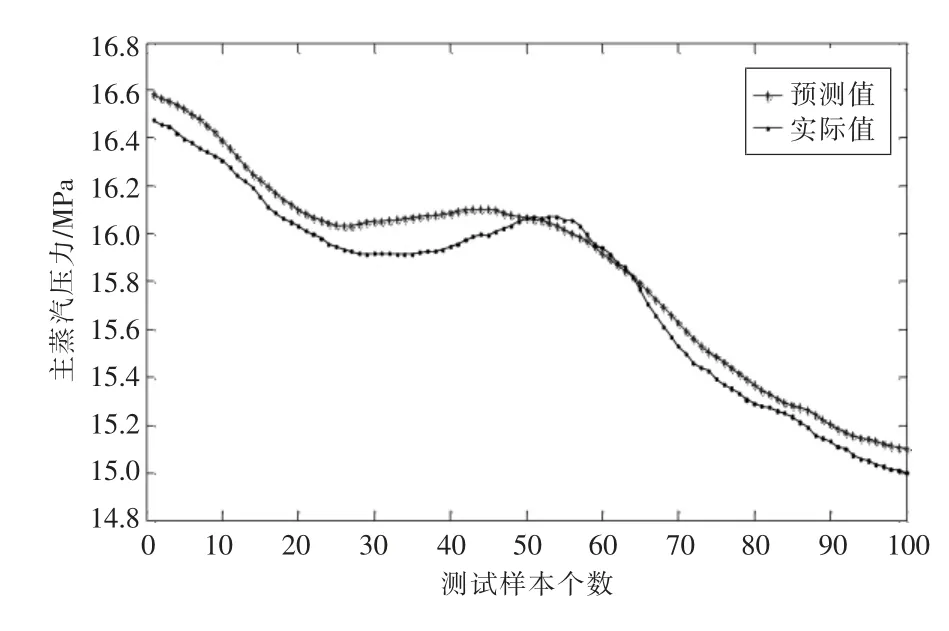
图8 测试阶段主蒸汽压力预测值与实际值对比

图9 测试阶段中间点温度预测值与实际值对比

决定系数R2一般用于评估回归模型预测值与实际值之间的符合程度，R 的定义如下：

式中：yi为真实数据；fi为预测值；为实际值的平均值，所以R2越接近1 越好。

相关系数评价2 个变量之间的相关性，定义如下：

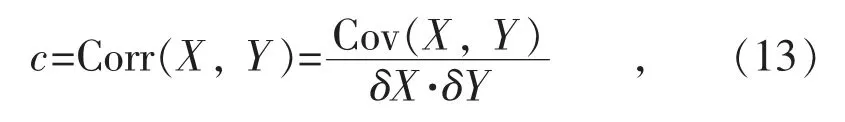
式中：Cov（X，Y）为协方差；δX，δY 分别是X，Y的标准差。

由表1 可以看出，PSO-DBN 模型相比DBN模型，在决定系数和相关系数上都具有良好的表现，但是在误差指标上都有不同程度的提高。PSO-DBN 模型机组负荷的δMAPE是0.42%，相比DBN 模型的1.43%降低1.01%；同样主蒸汽压力的δMAPE是0.6%，降低0.89%，中间点温度δMAPE为0.16%，降低了0.03%。δMAPE越小表示模型误差更小，在预测上具有更好的性能，因此，测试结果表明基于PSO-DBN 的机炉协调模型具有良好的非线性拟合能力，其预测精度满足工程要求。

表1 评价指标计算结果

5 结语

根据机炉协调系统非线性、强耦合的特点，以及机组内外部环境不断变化，模型特性容易变化，需要一种灵活的建模方法以适应机组未来智能化发展的需求。

本文提出了基于粒子群优化的深度置信网络的数据驱动建模方法，利用深度置信网络提取数据高阶特征，根据特征分布初始化网络初始参数。为了避免RBM 隐含层神经元数量随机设置影响模型精度，引入粒子群优化算法，最后结合BP神经网络构建记忆层。试验结果表明，该模型具有良好的非线性拟合能力，预测精度满足工程要求，为单元机组协调系统建模研究提供了一种新的可行方法。