基于HELM 网损灵敏度的配电网无功优化研究

赵亦岚，朱小燕，盛文洋，高慧敏，陈健琳

（1.杭州市电力设计院有限公司，杭州 310012；2.杭州电子科技大学 自动化学院，杭州 310018）

0 引言

配电网无功优化规划是一个满足约束条件下求取目标函数极值的复杂非线性优化问题，通常需要先确定补偿点，再用优化算法确定补偿量[1-7]。

通常采用灵敏度分析法来确定无功补偿点。采用灵敏度分析法选择配电网无功补偿点时，考虑到灵敏度往往与负荷相关，往往按补偿前潮流算出的灵敏度排序，得出的结果常常是同一条支路上相邻的几个节点，而这些高灵敏度节点中，一般只有一个节点是主节点，其余节点的灵敏度依赖于该节点潮流。当主节点加上无功补偿时，其他节点的灵敏度大幅下降。若将这些虚假的高灵敏度节点作为待补偿节点进行优化计算，则增大了寻优的搜索空间，加重了优化算法负担，难以得到最优解[8-9]。文献[8]提出采用二阶灵敏度矩阵来考虑系统的非线性特性及前后补偿节点的影响，一定程度上避免了选择虚高灵敏度节点，但它只考虑了二阶非线性特性，更高阶非线性特性难以求解。文献[9]采用的层次聚类方法也可以一定程度上避免选择虚高灵敏度节点。另外还有无功精确二次矩法、负荷功率阻抗矩法等方法，这些都是基于传统潮流的方法，可能存在潮流无法求解的情况，无法分离出线性灵敏度部分和各阶非线性灵敏度部分。

HELM（全纯函数嵌入方法）是最近提出的一种潮流计算方法，这种方法完全颠覆了传统的牛顿-拉夫逊法，它不依靠节点初始值，无需迭代，可以明确潮流解是否存在[10-12]。这种方法可以完全改变传统的电力系统潮流计算、无功优化、电压稳定分析等问题[13]，但如何利用HELM 计算网损灵敏度、进行无功优化目前尚无相关文献研究。

本文针对配电网无功补偿选点的灵敏度计算依赖潮流等非线性问题，提出了利用HELM 计算相关网损灵敏度的方法，并基于K-Means 聚类分析提出无功补偿选点的策略。通过28 节点配电网算例仿真分析，验证了该算法的有效性。相比文献[8-9]和其他方法，本文采用新的潮流计算方法，保证潮流确定可解，分离出了线性灵敏度和各阶非线性灵敏度，易于求解。

1 HELM 潮流计算方法

由节点功率方程建立配电网潮流计算的数学模型（除根节点外无PV 节点，根节点为平衡节点，假设无接地支路）：

式中：m 为PQ 节点集合，在配电网中除了根节点为平衡节点，其他节点均为PQ 节点；i，k 为节点号；Vi，Vk分别为节点i 和节点k 的电压；Yik为节点i、节点k 之间的导纳；Si为节点i 的注入功率；N 为节点总数；上标*表示共轭关系。

由于节点电压与节点注入功率等存在关系，而注入功率包括有功和无功，常用复数表示，全纯函数是复数分析方法，因此根据内嵌全纯函数方法，可以构造一个节点i 电压的内嵌纯虚函数：

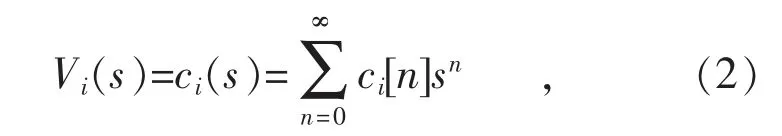
式中：s 为内嵌参数算子；ci（s）为i 节点的s 级数展开；n 为s 级数阶数；ci[n]为i 节点的电压的s级数n 阶项系数。

代入式（1）可得：

假设：

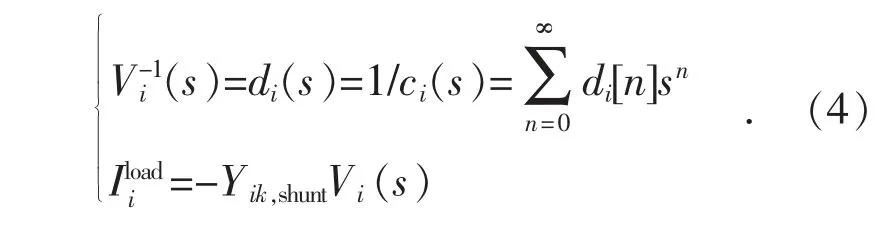
将式（2）和式（4）代入式（3）可得：

根据式（5）中s 级数的0 阶系数相等，可以得到：

由式（6）可以求出ck[0]。

根据式（7）中s 级数的0 次方系数相等，可以得到：

当s 阶数为1 时，由式（5）中s 级数的1 阶系数相等可得：

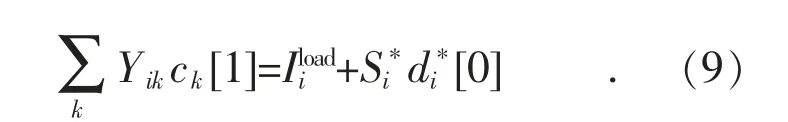
可以求出ck[1]。

由式（7）中s 级数的1 次方系数相等，可得：

求解可以得到dk[1]。

同理，逐步比较s 的n 次方级数的系数，逐步求解。

根据s 的n 次方级数的系数相等，由式（5）可知：

由式（7）中s 级数的n 次方系数相等，可得：

n 一直可以增加，可以逐步算出所有的ck[n]和dk[n]。

从而由式（2）可以得到Vi（s）。

当s=1 时，代入式（2），可以得到潮流的解，如式（13）所示。

2 利用HELM 潮流计算网损相关灵敏度

要想求得电压对节点注入有功功率和无功功率的灵敏度，也就是要求

由计算过程可知，ci[0]与注入功率无关，因此，均为0。

当j=i 时：

由式（12）可知：

由此推出：

同理，由式（11）方程两边对Pj，Qj求偏导，可以得到：

由前面算出的电压灵敏度就可以得到电力系统网损灵敏度，也可以得到每个部分的分项网损灵敏度。

分析可知，因为ck[0]恒定，dSSdQ（0）为0；与负荷无关，因此dSSdQ（1）与负荷无关；与负荷一次方成正比，因此dSSdQ（2）与负荷一次方成正比；与负荷二次方成正比，因此dSSdQ（3）与负荷二次方成正比；以次类推。

3 基于聚类和HELM 分项网损灵敏度确定配电网无功补偿点及容量

从前面推导可以看出，dSSdQ（2）与负荷一次方成正比，dSSdQ（3）与负荷二次方成正比，而且从后面仿真可以看出各分项网损灵敏度的排序一致，因此本文采用dSSdQ（2）来选择无功补偿节点。首先选择dSSdQ（2）网损灵敏度最大的节点；然后对各节点根据dSSdQ（2）灵敏度和文献[9]提出的负荷功率阻抗矩进行K-Means 聚类，如果该节点不在无功补偿集中，则根据网损最小确定补偿容量，比较网损的减少量是否小于设备的投资费用，如果小于则将该节点加入无功补偿集；确定无功补偿点后用遗传算法优化补偿容量，这样确定配电网无功补偿节点及对应的容量。计算流程如图1 所示。

4 算例分析

4.1 潮流计算结果分析

28 节点配电网单线图如图2 所示。支路参数和节点参数参照文献[8]。

从图3 中可以看出，HELM 潮流计算结果与前推回代法计算结果基本完全一致，是正确可行的。

图1 无功补偿优化流程

图2 28 节点配电网

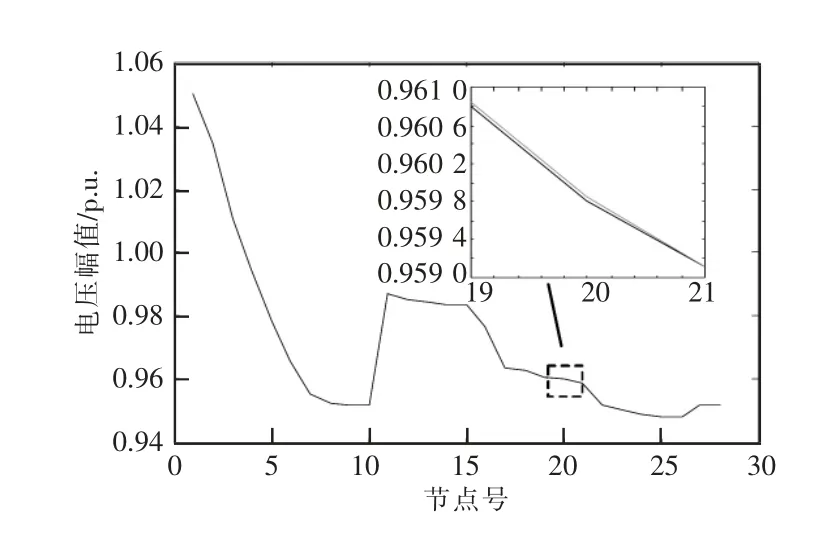
图3 2 种潮流计算结果对比

图4 28 节点网损无功灵敏度曲线

4.2 网损无功灵敏度分析

28 节点网损无功灵敏度如图4 所示。网损灵敏度通过扰动加以验证是正确的。

从图4 中可以看出，总的网损灵敏度dSSdQ与dSSdQ（2）接近，说明网损灵敏度主要受负荷的一次方影响更大。dSSdQ（1）很小，说明网损灵敏度受网络结构影响较小。dSSdQ（3）也会一定程度地影响网损灵敏度的数值。阶数越高，分项网损灵敏度越小。

另外，从图中还可以看出，dSSdQ，dSSdQ（2），dSSdQ（3），dSSdQ（4）网损灵敏度的节点排序基本一致，但计算dSSdQ（3），dSSdQ（4）等后面的灵敏度需要先计算dSSdQ（2），说明如果需要计算网损灵敏度排序来选择节点时，可只计算dSSdQ（2）等其中一项即可，大大提高了计算速度。各个网损灵敏度的计算时间如表1 所示。

表1 各个网损灵敏度计算时间比较

由表1 可知，计算dSSdQ（2）灵敏度时间为0.003 583 s，计算dSSdQ时间为0.102 979 s，时间缩短了20 多倍，系统越大，计算速度提高得越明显。

节点23，24，25，26 注入无功按照比例λ 变化，网损各项灵敏度如图5 所示。

图5 某些区域节点无功变化时网损无功灵敏度曲线

从图5 中可以看出，当节点23，24，25，26无功按照比例λ 变化时，dSSdQ 与dSSdQ（2），dSSdQ（3），dSSdQ（4）网损灵敏度变化趋势一致，可以采用dSSdQ（2）来分析网损灵敏度的变化趋势和排序。另外，当节点23，24，25，26 无功补偿增加时，这个区域的网损灵敏度得到显著提升，导致系统网损灵敏度排序发生改变，说明这种网损灵敏度改变有明显的区域性，因此可以根据这些值进行聚类分析选点。

结合dSSdQ（2）及文献[9]提出的负荷功率阻抗矩对28 节点配电网进行K-Means 聚类分析，并将28 个节点分成8 类，得到最佳聚类结果如图6 所示。

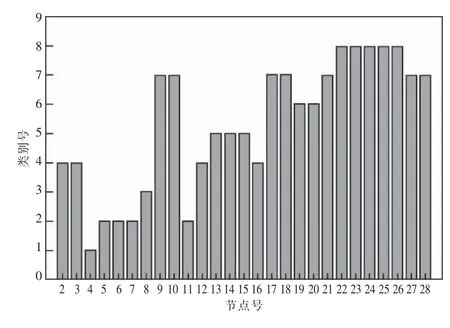
图6 28 节点聚类结果

由图可知：节点4 为第一类节点；节点5，6，7，11 为第二类节点；节点8 为第三类节点；节点2，3，12，16 为第四类节点；节点13，14，15 为第五类节点；节点19，20 为第六类节点；节点9，10，17，18，21，27，28 为第七类节点；节点22，23，24，25，26 为第八类节点。在上述各类节点中选出该类HELM 灵敏度最高的节点作为无功补偿点，并结合遗传算法计算出这8 个点的最佳补偿容量，如表2 所示。

表2 IEEE 28 配电网补偿节点及容量

利用本文提出的方法选择无功补偿点，将得到的无功优化结果与文献[8]、文献[9]方法进行比较，如表3 所示。

表3 IEEE 28 配电网结果比较

从表3 可以看出，采用本文所提方法得到的无功补偿容量更少，网损更低，从而验证了该方法的有效性。

5 结语

针对传统配电网无功优化在选择无功补偿点时存在的问题，基于HELM 推导了电压对功率的灵敏度和网损对功率的灵敏度的计算方法，并提出利用网损分项灵敏度来选择无功补偿装置安装位置的新方法。通过28 节点配电系统的仿真验算，并与传统灵敏度分析方法比较，验证了本文方法的有效性。与传统网损灵敏度计算方法相比，这种网损灵敏度计算方法具有潮流确定可解，计算速度快，可以得到与负荷成比例关系的分项灵敏度，如果网络结构不变则其结构灵敏度不变；如果网络结构改变，则可以通过修改导纳矩阵快速得到，其计算速度可以提高。