基于复合波形识别算法的“飞点”检测和还原方案研究

王瀚杰，黄棋悦，夏冰冰

（1.国网浙江省电力有限公司宁波供电公司，浙江 宁波 315000；2.宁波职业技术学院，浙江 宁波 315800）

0 引言

智能变电站在数字化变电站的基础上发展而来，采用先进、可靠、集成和环保的智能设备，利用信息的数字化、通信的网络化、信息的标准化，能够自动完成信息采集、测量、控制、保护、计量和检测[1]。同时，能够根据需求实现电网实时自动控制、智能调节、在线分析、协同互动等多个功能，是坚强智能电网建设中实现能源转化和控制的核心平台之一，代表了未来变电站的发展方向，具有广阔的应用前景[2-3]。

随着智能变电站的不断发展，SV（采样值）智能设备得到了广泛应用。但近年来，因采样数据异常、波形中出现“飞点”（数据异常点）等情况，智能变电站站域保护装置误动或者拒动现象时有发生。如500 kV 菊城变、500 kV 夏金变、330 kV唐乃亥变等高电压等级变电站，一旦发生保护误动现象，就会危害整个电力系统的稳定运行，甚至导致系统解列[4]。

由于智能变电站的建设时间还不长，目前国内外对“飞点”识别方法的研究较少，且都存在一定的不足。例如，基于可去间断点的连续采样“飞点”检测算法，通过数学函数连续性及可去间断点的定义得到“飞点”判据，该判据虽然能准确识别“飞点”数据，但仅限于单个“飞点”的情况，对于连续“飞点”判断能力不足。传统的识别方法普遍具有针对性不强、灵敏度不高、数据窗过长、数据无法恢复等缺陷。在“飞点”识别后也仅仅作闭锁处理，虽能保证保护不拒动，但发生故障后的速动性也受到了挑战[5-6]。

对此，本文提出一种基于复合波形识别算法的“飞点”检测和还原方案。首先分析了智能变电站中“飞点”产生的原因和机理，并归纳总结了国内外的“飞点”识别方案优缺点[7-8]。在此基础上，提出了复合波形识别算法，比较波形及其导数波形的相似程度，计算相似系数，识别波形“飞点”。再通过正弦恢复算法可将“飞点”数据修复。最后通过PSCAD/EMTDC 仿真实验证明，该方案能够正确识别单个“飞点”和连续“飞点”的电流波形，修复后的波形不会导致继电保护误动或拒动，满足了站域保护的要求，验证了该方案的可靠性。

1 方案比较

对现场出现的大量异常数据进行整理，并查阅有关文献发现，SV 中“飞点”产生的机理非常复杂，主要原因有：电子式互感器电源异常影响合并单元的识别，造成数据的无效化；因外界因素导致合并单元和电子式互感器之间通信中断，无数据传输；电磁干扰造成数据异常，进而形成“飞点”；因芯片工艺和算法设计问题形成“飞点”。为治理以上问题，国内外学者开展了大量研究和仿真工作，主要对策有延迟动作方案、双重采样数据方案、“飞点”识别算法方案等。

1.1 延迟动作方案

修改保护装置的动作时间，使其延迟动作：当保护的延迟时间大于“飞点”可能出现的最大时间时，保护不会发生误动情况。该方案在保证保护装置可靠性的同时，一定程度上牺牲了速动性，仅适用于部分对动作时限要求不高的设备。但智能变电站一般电压等级较高，要求保护能够立刻动作，因此该方案存在一定的局限性[9]。

1.2 双重采样数据方案

增设一路AD 采样数据，采用双重采样数据进行保护的判别[10]。保护装置2 路AD 采样数据均满足动作判据时才会动作。若只有1 路AD 数据满足，则保护闭锁、不动作。该方案在只有1路数据出现“飞点”时，仍能够保持闭锁，具有较高的可靠性。但会导致保护的动作变慢，在浪涌情况下仍有出现误动的可能性，存在一定的不足。

1.3 “飞点”识别算法方案

在保护装置内部增添一套“飞点”识别算法，有效识别波形中的“飞点”信号，发出闭锁信号，保证装置不误动。以下对积分型波形识别法和导数型波形识别法进行简单介绍[11-12]。

（1）积分型波形识别法

当线路发生短路故障时，保护装置测得的故障电流与标准正弦波相似。“飞点”具有无序性的特点，出现“飞点”的波形将不同于标准正弦波。因此，可以通过比较波形第1 个半周期和第2 个半周期的相似程度来判断电流的类型。设波形第1 个半周期的面积为S+，第2 个半周期的面积为S-，计算出波形对称系数如下：

当没有“飞点”产生时，正常运行和短路故障时的波形对称型系数Ksym=0，而产生“飞点”后的短路故障波形中Ksym≫0。通过比较波形对称系数，可以实现“飞点”的识别。

（2）导数型波形识别法

导数型波形识别法是一种基于电流半波对称导数比较的算法。该算法的基本思想是用导数法求出无直流分量的差动电流，然后比较微分电流的上、下半波形是否对称。公式如下：

式中：Ii为前半个波形中某个点的值；Ii+180°为下半个波形中对应点的值。与积分型波形对称法相似，也是通过比较波形对称系数Ksym来实现“飞点”的识别。

2 复合波形识别方案

上文研究了“飞点”识别的产生机理和解决方案，并举例说明了“飞点”识别算法的原理。然而，这些方法存在着速动性不足、可靠性不够等问题。针对以上问题，为了提高“飞点”识别的准确性，加速保护的动作时间，降低可能的降级损失，本文提出了基于复合波形识别算法的“飞点”检测和还原方案。该方案采用复合波形识别算法实现“飞点”数据的判别，再通过正弦还原法对“飞点”数据进行还原处理[13-15]。

2.1 复合波形识别原理

图1 为发生短路故障时的电流波形，图2 为对该电流波形进行微分处理后的微分波形。可以看出，故障电流波形及其导数波形与标准正弦信号相似程度高。假设故障电流的方程如下：

式中：Am为电流的幅值；ω 为电流的频率；t 为时间；θ 为初始相位角。

图1 故障电流波形

图2 故障电流微分波形

对式（3）进行微分处理后，得到微分波形的方程为：

由式（4）可以看出，故障电流的微分波形与正弦波形的公式基本相同。因此，可以将该波形单位化后，与标准正弦波进行比较。若形状相似，则可以判断为故障电流值，无“飞点”数据。若形状不相似，则可以判断为出现“飞点”数据。根据积分波形对称原理，给出波形对称系数如下：

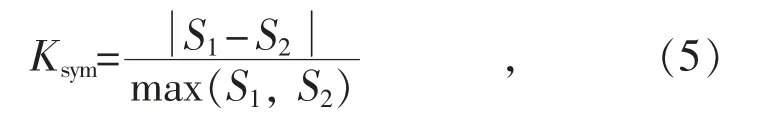
式中：S1为一定时间窗内微分电流波形的面积；S2为一定时间内标准正弦波形的面积。Ksym=0 时，波形无“飞点”数据；Ksym≫0 时，波形有“飞点”数据。

2.2 正弦修复原理

若判断波形含有“飞点”数据，采用正弦恢复方法对波形进行修复。将测量电流波形数据按照正弦信号的理想波形进行修复，公式如下所示：

式中：Ik为波形中出现的“飞点”数据；Isin·k为该点数据所对应的正弦信号的数据值。用正弦信号值代替出现的“飞点”数据，即可实现波形的修复。

2.3 方案流程

基于复合波形识别算法的“飞点”检测和还原方案，就是利用复合波形计算波形对称系数，从而实现对“飞点”数据的识别。判断有“飞点”数据后，采用正弦修复方法，用正弦信号量代替“飞点”数据量，实现波形的修复。修复后，进行故障判别，若为短路故障，保护动作；若非短路故障，保护不动作。判断无“飞点”数据后，直接进入故障判别环节。具体的方案流程如图3 所示。

3 仿真验证

3.1 异常数据检测

本文采用PSCAD 仿真软件搭建了简单的电力系统模型，用于验证基于复合波形识别算法的“飞点”检测和还原方案在电力系统中的可行性。仿真结果如表1 所示。

图3 飞识识别流程

表1 保护装置动作情况表

表1 中，方案A 为基于复合波形识别算法的“飞点”检测和还原方案，方案B 为其他保护方案，共进行了5 组仿真实验。可以看出，5 组仿真数据中，未采用波形识别方案的保护装置在正常运行时容易发生误动，而在短路故障时可能发生拒动。而采用基于复合波形识别算法的“飞点”检测和还原方案能够保证保护装置的可靠性，使其不误动、不拒动。

图4、图5 分别为出现单个“飞点”的波形和经正弦修复后的波形。可以看出“飞点1”“飞点2”“飞点3”能够被正确修复，仿真验证了方案A 可以减少单个“飞点”对继电保护的影响。

图6、图7 分别为出现持续“飞点”的波形和经正弦修复后的波形。可以看出“飞点”群能够被正确修复，仿真验证了方案B 可以减少多个“飞点”对继电保护的影响。

图8、图9 分别为出现丢点的波形和经正弦修复后的波形。可以看出丢点能够被正确修复，仿真验证了该方案可以减少丢点对继电保护的影响。

图4 单个飞点波形图

图5 单个飞点波形修复

图6 持续飞点波形

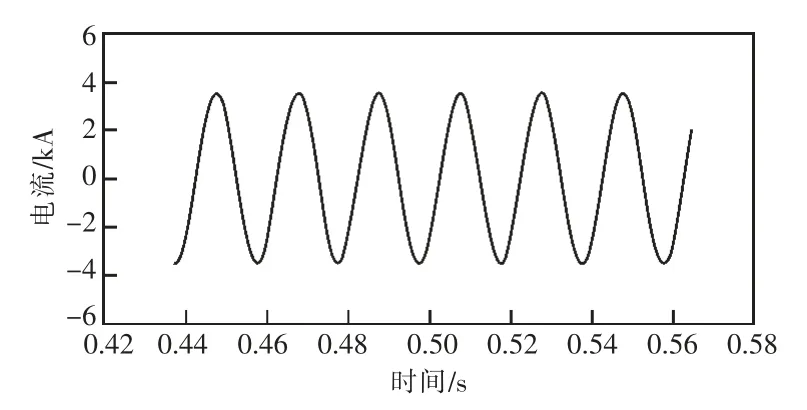
图7 持续飞点波形修复

图8 丢点波形

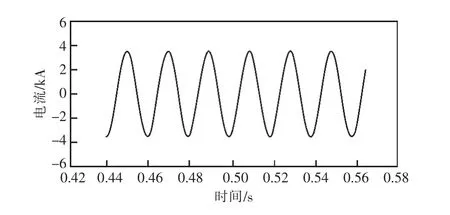
图9 丢点波形修复

复合波形识别算法根据图3 所示流程对波形进行修复后，再判别故障类型。若为短路故障，则保护装置正常动作，不发生拒动。若为正常运行时电流，则保护正常不动作，不发生误动。仿真验证了该方案可以减少异常数据对继电保护的影响。

3.2 动作时限检测

将采用基于复合波形识别算法的“飞点”检测和还原方案的保护装置动作时间与采用其他传统方案保护装置的动作时间进行仿真比较，得到结果如表2 所示。

表2 保护装置动作时限

表2 中共4 组仿真数据，方案A 为基于复合波形识别算法的“飞点”检测和还原方案，方案B为未采用任何“飞点”识别算法的方案，方案C 为采用导数型波形识别法方案，方案D 为采用积分型波形识别法方案。可以看出，本文所提方案A动作时限较快，不会影响继电保护正常动作。

4 结论

智能变电站采用数字化采样的方式，SV 中大幅值“飞点”的出现导致保护误动，危害变电站和电力系统的稳定运行。为解决“飞点”识别困难的问题，本文提出了基于复合波形识别算法的“飞点”检测和还原方案，并得出如下结论：

（1）利用复合波形识别算法对所测电流值进行求导处理，得到其导数波形，再将波形单位化后与标准正弦波进行比较，计算波形相似系数K。若测量波形无“飞点”，则波形相似系数K=0；若测量波形有“飞点”，则波形相似系数K≫0。通过比较波形相似系数，实现“飞点”的识别。

（2）正弦还原算法将之前测出的“飞点”值进行还原。使用正弦信号量代替“飞点”数据来对波形进行还原，可以实现单个或多个“飞点”群的还原，无需闭锁判据，保证了保护装置的可靠性和速动性。

（3）通过建立PSCAD 仿真模型对所提方案进行分析研究。实验证明，正常运行时、故障运行时的“飞点”数据都能够被正确识别和还原。正常运行时，若波形出现单个“飞点”、多个“飞点”、丢点，保护装置不动作，不会误动。故障运行时，若波形出现单个飞点、多个“飞点”、丢点，保护装置正常动作，不会拒动。通过对动作时限的仿真验证，发现保护装置动作迅速，速动性得到保证。

理论分析和实验验证均显示，该方案具有较高的可靠性和应用性。随着我国变电站的推广，该方案具有良好的应用能力和研究潜力。