干式空心电抗器的试验模态特征分析∗

张嵩阳 何 强 肖伟民 王磊磊 王东晖

(1 国网河南省电力公司电力科学研究院 郑州 450052)

(2 先进输电技术国家重点实验室(全球能源互联网研究院有限公司) 北京 102209)

(3 北京市劳动保护科学研究所 北京 100054)

0 引言

近年来，随着我国城市化进程的快速发展，变电站周边居民小区日益增加，变电站噪声扰民问题日益突出。干式空心电抗器作为变电站内重要声源设备，对变电站周边声环境具有较大影响。根据以往研究结果[1]，干式空心电抗器噪声主要来源于交流电流和谐波电流相互作用引起的线圈振动，其工作状态下的声压级一般可达60 dB(A)以上，因而需要对其采取有效降噪措施来降低噪声水平。

然而，国内以往对其噪声控制方面的研究相对较少，目前主要致力于结构参数(包封数、内径、线径等)的优化设计[2−4]，以期获得更加合理的电流分布、较低的损耗和良好的温升，但在结构设计的同时并未充分考虑电抗器的振动噪声水平，致使无法实现干式空心电抗器的整体性能最优。由于结构降噪的研究不足，也使得干式空心电抗器在后期采用一些降噪措施后，不但降噪效果十分有限，还引发了很多技术冲突，这些问题已严重制约了干式空心电抗器的发展[5]。因此针对干式空心电抗器噪声控制研究还存在很多工作需要开展。其中，对干式空心电抗器进行模态动力学分析，是开展干式空心电抗器降噪设计与应用降噪措施的前提基础。模态分析是以振动理论为基础、以模态参数为目标的分析方法，可以得到设备结构具有的特定固有频率和模态振型，从而有效掌握设备的动力学特性，进而为设备的降噪设计提供基础，为避免设备共振提供重要支撑。

但目前，针对干式空心电抗器模态动力学特性的试验研究工作仍然不够充分，姜志鹏[6]采取block Lanczos 模态提取法获得了干式空心电抗器整体设备的前1000 阶模态，宋新伟[7]通过实验和仿真得到了干式空心电抗器整体设备的自由模态，并仿真分析了结构参数对干式空心电抗器自由模态的影响，Verbruggen等[8]对干式空心电抗器整体设备的结构模态进行了计算和测量，上述模态实验研究工作均是针对设备整体进行计算或者分析，并未针对设备每个组件进行单独试验研究[6−8]，致使很难准确地为干式空心电抗器的降噪设计提供有效支撑[5]。鉴于此，本文主要研究干式空心电抗器的模态动力学特性，通过对绕组、支柱和整体设备的模态试验和分析，掌握其固有频率和模态振型，从而为干式空心电抗器结构的降噪改进工作提供有效指导。

1 模态分析与试验方法

1.1 特征系统模态分析方法

在模态分析方法中，特征系统实现方法是一种基于多输入多输出的时域模态识别方法，具有模态识别准确率高、计算效率高的优势。当模态频率较密集时，该方法可将频响函数逆变换得到脉冲响应函数，比一般频域识别方法具有更好的识别效果。该方法最早由美国航天局提出[9−11]，并已成功应用于多个领域的模态识别工作上。

特征系统实现方法的基本思想是利用矩阵奇异值分解(Singular value decomposition,SVD)技术，对实测自由脉冲响应数据矩阵进行分解，通过截断无效奇异值，来实现状态空间最有效数目的参数控制。其本质是一种时域参数辨识方法。下面就特征系统算法的实现过程给出简单说明。

当系统振动时，力的平衡关系可以表示为

其中，M为系统的质量阵，C为系统的阻尼阵，K为系统的刚度阵，Bf为输入分配矩阵，x为系统质点位移，t为时间，y为与时间相关的函数。

将上述系统振动平衡方程(1)写成状态方程的形式(2)，即

当系统结构未发生变化时，系统矩阵和控制矩阵均为常数矩阵，因而可以获得一组一阶常微分方程组，可得

式(3)中，t为时间，t0为初始状态时间。若使用等间隔采样，再加之零阶保持器在一个采样间隔内采样值不变的特性，可得

式(4)中，k为间隔数，T为时间周期。通过式(4)就可以得到系统离散时刻的脉冲响应矩阵公式(5)，如下所示：

这样就有系统的Hankel矩阵如式(6)所示：

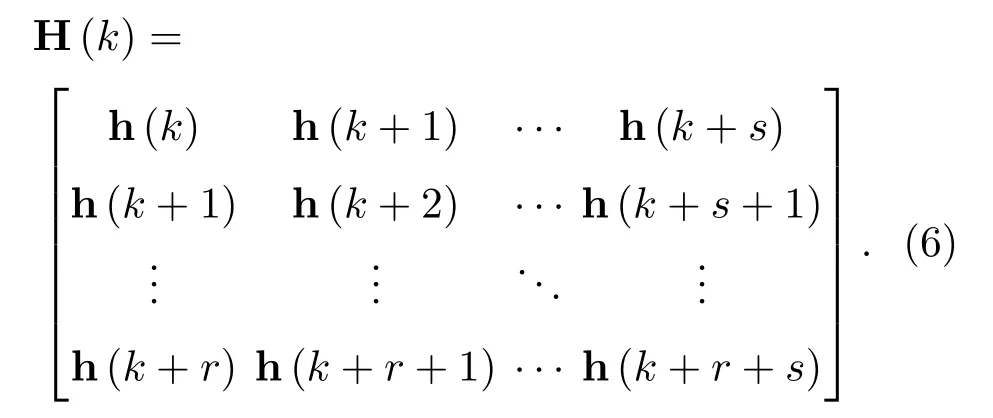
将H(0)做奇异值分解，选取前r个最大奇异值对系统进行缩减，最终可得系统的脉冲响应函数为

其中，Pr、Qr为正交矩阵中对应前r个最大奇异值的SVD 分解的列，Dr为r个最大奇异值组成的对角矩阵，Ip为p阶单位矩阵，p为输出向量的维数。

由此可得，系统的最小实现为

通过上述特征系统方法进行系统实现，就可以系统实现所求解系统的模态参数，从而直接对系统矩阵A进行特征分解，得到干式空心电抗器动力学系统的固有频率。

1.2 试验分析方法

基于模态分析的基本原理，本次试验对干式空心电抗器本体结构进行了模态试验分析，干式空心电抗器采用了目前变电站常用的PKDGKL-300 型产品，电抗器高4670 mm，外径5140 mm，试验采用Coinv DASP模态分析软件和INV3020C 多通道采集分析仪，利用力锤移动激励的多点激振单点拾振方法开展模态试验，电抗器结构和试验流程图如图1、图2所示。

图1 干式空心电抗器外形结构Fig.1 Dry-type air-core reactor configuration

图2 干式空心电抗器模态试验流程图Fig.2 Flow chart of dry-type air-core reactor modal test

模态试验的绕组力锤锤击测点共设置40个，在圆周方向上每隔45◦设置1 列测点，每列设置5 个测点，每个测点分轴向和切向两个方向激励；模态试验的支柱力锤锤击测点共设置40个，在圆周方向上每隔45◦设置1 列测点，每列设置5 个测点，每个测点分轴向和切向两个方向激励。在此基础上，利用Coinv DASP 模态分析软件，按照电抗器尺寸分别对绕组和支柱进行结构建模，其模型如图3所示，并按激励力方向输入锤击响应加速度。

利用上述脉冲响应矩阵公式(5)、Hankel 矩阵公式(6)，代入激励力与响应值，将力与加速度响应信号转换成速度频响函数，通过逆快速傅里叶变换(Fast Fourier transformation,FFT)得到脉冲响应函数，并获得系统脉冲响应函数的最小实现式(8)，从而得到系统的模态固有频率和振型。将振型数据代入上述电抗器模态试验模型中，可得到可视化振型结果。

图3 电抗器模态试验模型Fig.3 Modal test model of the dry-type air-core reactor

2 模态分析结果

2.1 绕组的模态动力学特征

通过应用上述特征系统模态分析方法获得干式空心电抗器绕组的前5阶固有频率，如表1所示。

表1 干式空心电抗器绕组前5 阶固有频率Table 1 The first 5 natural frequencies of the dry-type air-core reactor winding

同时，利用模态试验分析方法得到的较为关键的第3 阶、第4 阶、第5 阶模态振型，如图4 所示。从模态分析结果可见，固有频率在100 Hz、150 Hz、200 Hz 附近存在与电抗器实际运行工况噪声频谱相近的固有频率，易于引发结构共振。其中第3 阶模态振型主要表现为沿绕组径向运动的弯扭变形特征，第4 阶模态振型主要表现为沿绕组轴向运动的弯扭变形特征，变形使电抗器中心平面向轴向对称压缩，第5 阶模态振型主要表现为沿绕组轴向运动的弯扭变形特征。

2.2 支柱的模态动力学特征

干式空心电抗器支柱前5阶的固有频率，如表2所示。

图4 干式空心电抗器绕组的关键阶次模态振型Fig.4 Key mode modes of the dry-type air-core reactor winding

同时，利用模态试验分析方法得到的较为关键的第1 阶、第3 阶模态振型，如图5 所示。从模态分析结果可见，支柱的固有频率在50 Hz、100 Hz附近存在与电抗器实际运行工况噪声频谱相近的固有频率，易于引发结构共振。其中第1 阶振型主要以一阶弯曲变形为特征，第3 阶振型主要以支柱底部弯曲扭转变形为主要特征，对电抗器振动增强具有一定的影响。

表2 干式空心电抗器支柱前5 阶固有频率Table 2 The first 5 natural frequencies of the dry-type air-core reactor support structure

图5 干式空心电抗器支柱的关键阶次模态振型Fig.5 Key mode modes of the dry-type air-core reactor support structure

2.3 整体设备的模态动力学特征试验

干式空心电抗器整体设备的前5 阶固有频率，如表3所示。

同时，利用模态试验分析方法得到的前4 阶模态振型，如图6 所示。从模态分析结果可见，干式空心电抗器设备整体结构的固有频率在50 Hz、100 Hz、150 Hz 附近存在与电抗器实际运行工况噪声频谱相近的固有频率，易于在激励力作用下容易引发电抗器整体结构共振。其中，第1阶模态振型主要表现为整体结构的弯曲变形为主的振动变形特征，第2 阶模态振型表现为结构的弯扭变形和扭摆变形特征，第3 阶模态振型表现为结构的扭转变形特征，第4 阶模态振型表现为结构的弯扭变形特征。随着干式空心电抗器整体结构阶次的升高，其模态振型特征逐渐由弯曲变形向多阶弯扭变形转变，显示出更为复杂的变形特征。

在干式空心电抗器结构中，设备伸缩变形和弯曲扭转变形对结构整体的共振效应起到关键作用。其前4 阶模态的固有频率较低，与设备运行时的一些重要振动噪声频段比较靠近[5,12]。

表3 干式空心电抗器前5 阶固有频率Table 3 The first 5 natural frequencies of the dry-type air-core reactor

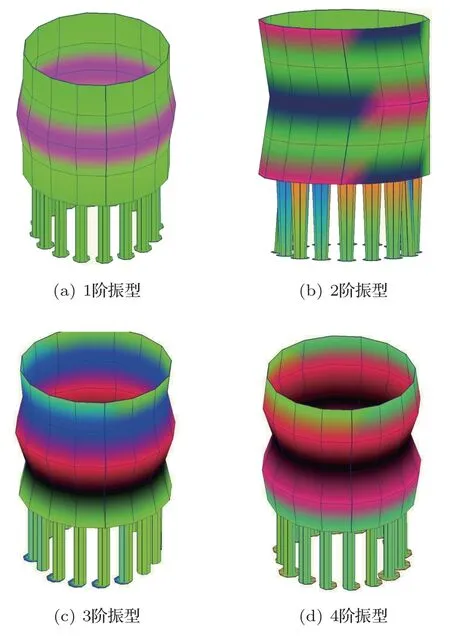
图6 干式空心电抗器整体设备的前4 阶模态振型Fig.6 Key mode modes of the dry-type air-core reactor

在实际通电运行过程中，干式空心电抗器在电流作用下容易发生结构共振，最终可能导致电抗器结构振动加大，在结构内部形成振动增强和放大作用，大幅提升结构噪声水平。另外，结构各位置在变形条件下容易出现应力集中，在弯曲和扭转变形下也易于引发设备变形和损坏。有鉴于此，建议在今后的研究中，针对干式空心电抗器易于发生变形的位置，利用降噪阻尼材料或进行结构改进，改变设备的模态特征，使其远离通电状态下的主要作用频段，避免通电运行状态下设备共振的发生，同时降低共振对设备的损坏能力，进而保证设备的安全运行，提高设备的环保水平。

3 结论

本文利用特征系统模态分析方法，对干式空心电抗器绕组、支柱和整体设备的模态特征进行试验和分析，电抗器绕组的前5 阶模态固有频率主要集中在35.5 Hz、82.3 Hz、101.7 Hz、149.5 Hz、202.4 Hz，支柱的前5 阶模态固有频率主要集中在43.4 Hz、73.2 Hz、96.0 Hz、121.0 Hz、167.9 Hz，电抗器整体的前5 阶模态固有频率主要集中在12.85 Hz、33.78 Hz、48.87 Hz、98.62 Hz、146.63 Hz，其中电抗器绕组、支柱和整体设备模态固有频率与通电时电抗器的振动峰值频率100 Hz 和200 Hz 较为接近，易于引发设备共振，进而增加设备噪声水平并影响设备正常运行。因此，可考虑针对设备关键位置应用降噪阻尼材料或结构设计来改变设备的低阶固有频率，进而避免通电激励下设备发生共振。