基于内啮合齿轮副设计的辐射治疗头圆弧提升运动机构*

□ 郭 召

西安大医集团股份有限公司 西安 710018

1 设计背景

辐射治疗头是一种大型放射治疗设备的关键部件,专用于对肿瘤进行精准放射治疗。辐射治疗头安装在旋转机架上,随旋转机架回转。在治疗过程中,辐射治疗头还需要沿滚筒轴向摆动,摆动圆心位于旋转机架回转轴线上。辐射治疗头内部包含大量铅和钨,质量非常重。为了保证辐射治疗头圆弧运动的平稳性和定位的准确性,笔者设计了辐射治疗头圆弧提升运动机构,能够提升整机性能。

在大模数齿轮啮合强度方面,冯定等[1]对大模数重载齿轮齿条的接触强度进行了研究,李倩等[2]基于ANSYS Workbench软件对回转机构回转齿圈接触进行了有限元分析,常乐浩等[3]结合有限元法和接触理论对内啮合齿轮副啮合刚度进行了计算,关锋[4]对内啮合齿轮接触应力进行了有限元分析,徐金波等[5]对直线共轭内啮合齿轮副啮合强度进行了分析,黄靖龙等[6]分析了压力角对齿轮强度的影响。现有文献对齿轮齿条副提升运动及齿轮啮合强度的研究较多,对内啮合齿轮副圆弧提升运动的研究则较少。笔者对复合运动状态下内啮合齿轮副的受力状态进行分析,设计了辐射治疗头圆弧提升运动机构,对内啮合齿轮副中的齿根弯曲应力进行了理论计算及有限元分析。

2 设计方案

辐射治疗头安装在滚筒上,随滚筒一起旋转,同时自身相对滚筒有摆动运动。辐射治疗头结构如图1所示,由一对弧形导轨支撑,滚筒上安装有圆弧齿条。滚筒上安装驱动组件,驱动组件输出轴上的驱动齿轮与圆弧齿条啮合,使辐射治疗头实现往复摆动。另一方面,滚筒带动辐射治疗头绕自身回转轴线转动,辐射治疗头的摆动方向与滚筒的旋转方向成正交关系。

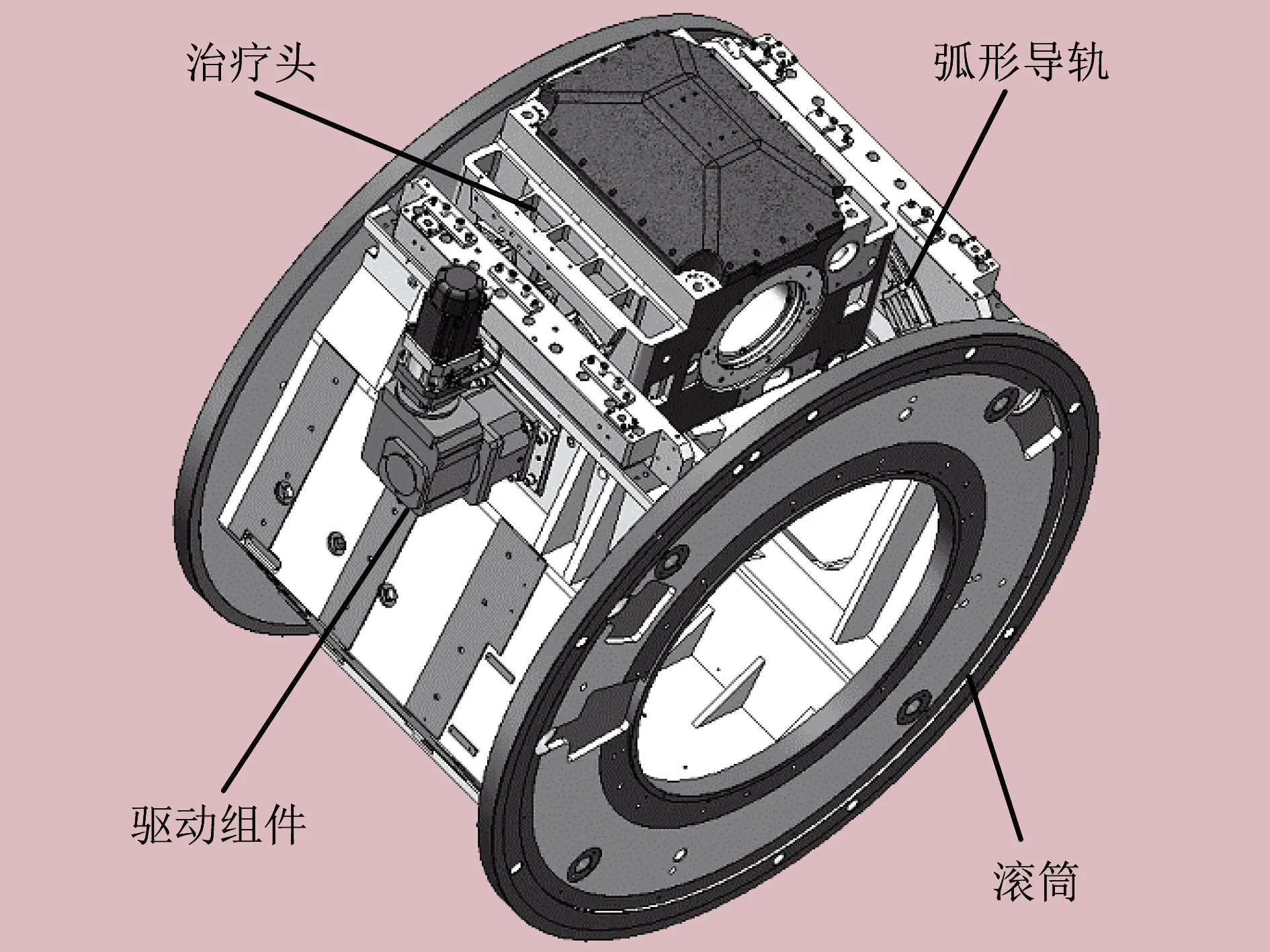
图1 辐射治疗头结构

3 受力分析

辐射治疗头由弧形导轨支撑,由内啮合齿轮副驱动,进行0°～15°摆动。驱动齿轮主要承受由辐射治疗头重力引起的扭矩。当滚筒静止时,随着辐射治疗头的摆动,齿轮上承受的扭矩按正弦规律产生变化。当滚筒旋转时,辐射治疗头随滚筒一起做回转运动,辐射治疗头作用在摆动方向上驱动齿轮的扭矩随之变化。在滚筒进行360°旋转时,重力作用在驱动齿轮上的方向发生周期性变化,产生冲击,齿侧间隙是产生冲击的主要原因。辐射治疗头摆动到位后静止,此时驱动齿轮和圆弧齿条处于静态啮合状态。辐射治疗头摆动如图2所示。

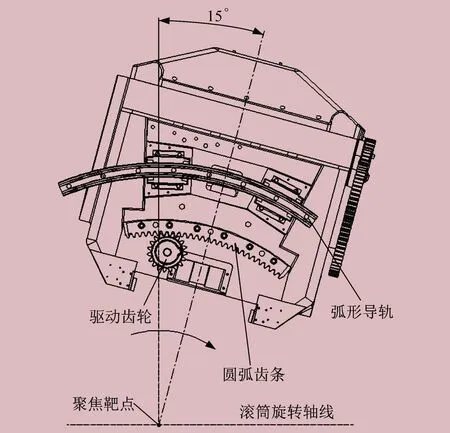
图2 辐射治疗头摆动示意图

在滚筒旋转过程中,内啮合齿轮副的受力发生周期性变化。当滚筒旋转角度为0°时,辐射治疗头处于最顶部,驱动齿轮的回转轴线与地面平行,此时驱动齿轮承受由辐射治疗头重力分力所产生的扭矩。当滚筒旋转角度为90°时,辐射治疗头处于水平位置,驱动齿轮的回转轴线垂直于地面,此时驱动齿轮不承受由辐射治疗头重力产生的扭矩。当滚筒旋转角度为180°时,辐射治疗头位于最底部,驱动齿轮的回转轴线与地面平行,此时驱动齿轮上承受由辐射治疗头重力分力所产生的扭矩,扭矩方向与滚筒旋转角度为0°时相反。当滚筒旋转角度为270°时,辐射治疗头处于水平位置,驱动齿轮的回转轴线垂直于地面,此时驱动齿轮不承受由辐射治疗头重力产生的扭矩。

辐射治疗头在随滚筒回转过程中摆动时,驱动齿轮受力分析如图3所示。当滚筒处于任意位置时,辐射治疗头施加在驱动齿轮上的扭矩由辐射治疗头重力G沿弧形导轨切向方向的分力F引起,F为:

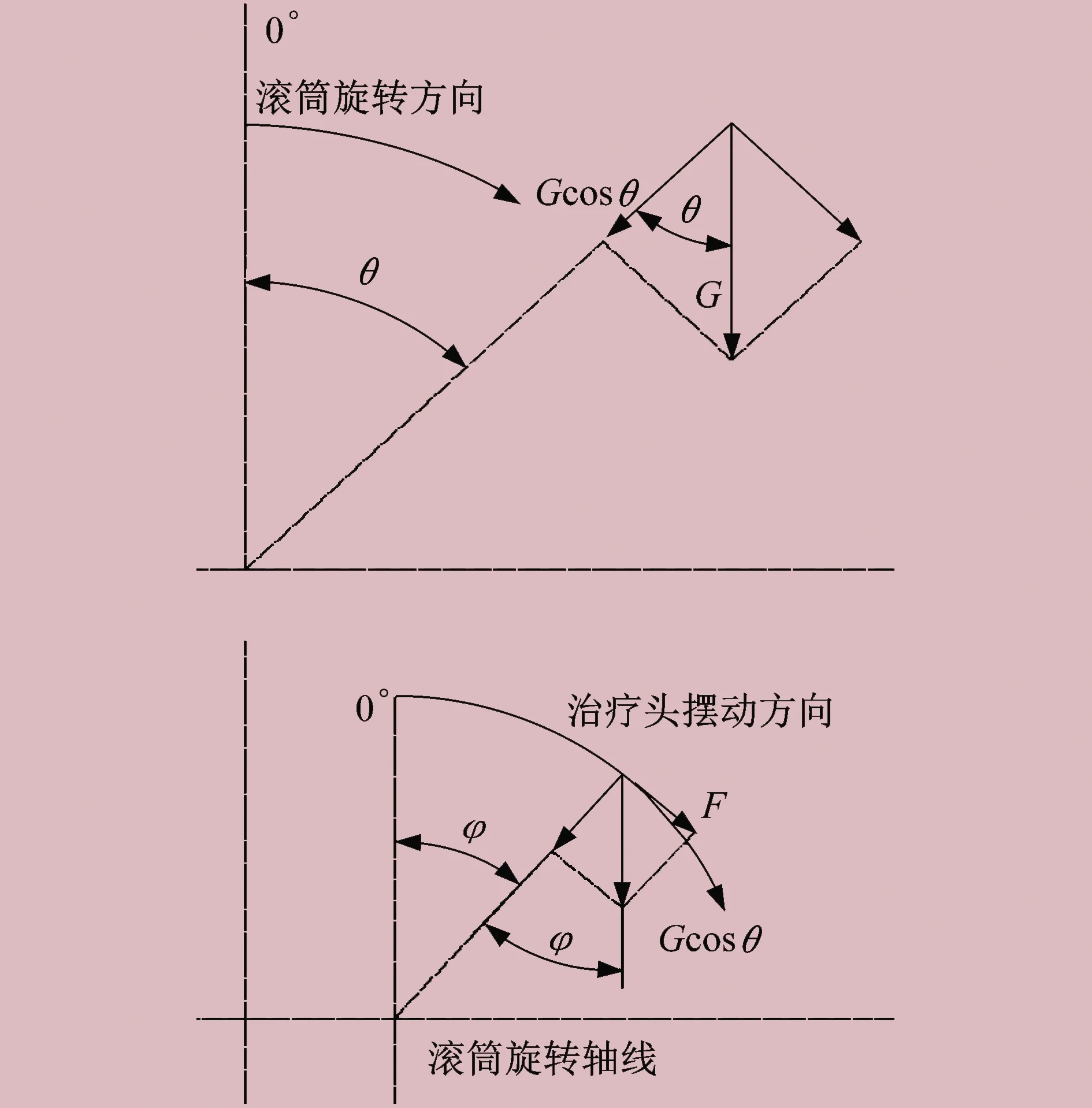
图3 驱动齿轮受力分析

F=Gcosθsinφ

(1)

式中:θ为滚筒的旋转角度;φ为辐射治疗头的摆动角度。

通过数学模型分析可以得到,随着辐射治疗头摆动角度的增大,驱动齿轮上的扭矩呈现增大变化。滚筒的旋转对驱动齿轮上的扭矩产生周期性变化影响,在0°～90°范围内,扭矩逐渐减小;在90°～180°范围内,扭矩逐渐增大;在180°～270°范围内,扭矩逐渐减小;在270°～360°范围内,扭矩逐渐增大。当辐射治疗头位置摆动到位锁定后,φ为常数,那么随着滚筒的旋转,施加在驱动齿轮上的扭矩按余弦规律波动。当滚筒位置固定后,θ为常数,那么随着辐射治疗头的摆动,施加在驱动齿轮上的扭矩按正弦规律波动。

4 内啮合齿轮副计算

辐射治疗头重力G为40 kN,由内啮合齿轮副驱动,产生摆动。对内啮合齿轮副进行设计,首先要考虑其强度,以保证安全性。另一方面,在辐射治疗头摆动范围内,要求在任意位置准确停止,定位精度高于0.01°。内啮合齿轮副需要同时完成动力及精度的传递,要求内啮合齿轮副在设计时兼顾强度、精度、稳定性,以及安装空间的限制。

在工作过程中,施加在内啮合齿轮副上的最大切向载荷Fmax为:

Fmax=Gcosθsin15°≈10 352 N

圆弧齿条摆动半径r为600 mm,那么作用在圆弧齿条上的最大工作扭矩Mmax为:

Mmax=rFmax=0.6×10 352≈6 211 N·m

根据《齿轮手册》[7]对内啮合齿轮副的模数m进行计算,m为:

(2)

式中:Am为计算因数,Am=12.6;K为计算载荷因数,K=1.221;T1为辐射治疗头驱动扭矩,T1=590 N·m;YFS为复合齿形因数,YFS=5.44;φd为齿宽因数,φd=0.57;Z1为驱动齿轮齿数,Z1=19;σFP为许用齿根应力,内啮合齿轮副低速重载时,按齿根弯曲疲劳极限确定,σFP=525 MPa。

计算得m≥4.17 mm,取m为6 mm。

辐射治疗头的摆动为低速间歇运动,根据《齿轮手册》[7]对内啮合齿轮副基于齿根弯曲强度进行校核。

齿根应力σF为:

(3)

式中:Ft为切向载荷,取Ft=10 352 N;Yεβ为重合度,Yεβ=0.66;b为尺宽,b=65 mm;mn为齿轮法向模数,取mn=6 mm。

计算得σF为116 MPa。内啮合齿轮副在最大受力状态下的安全因数SFmin为:

SFmin=σFEYNTYδrelTYRrelTYX/σF

(4)

式中:σFE为弯曲疲劳极限,σFE=1 050 MPa;YNT为寿命因数,YNT=1;YδrelT为相对齿根圆角敏感因数,YδrelT=1;YRrelT为相对齿根圆角表面状况因数,YRrelT=0.9;YX为尺寸因数,YX=1。

计算得SFmin为8.12,满足医疗设备对悬挂物8倍强度安全因数的要求。

5 有限元分析

应用SolidWorks软件创建内啮合齿轮副三维模型,如图4所示。对内啮合齿轮副按啮合状态施加机械约束,保存为.igs格式文件后导入有限元分析软件,添加材料属性[8-9]。驱动小齿轮和圆弧齿条的材料均为17CrNiMo6,弹性模量为200 GPa,泊松比为0.3,屈服强度为835 MPa。

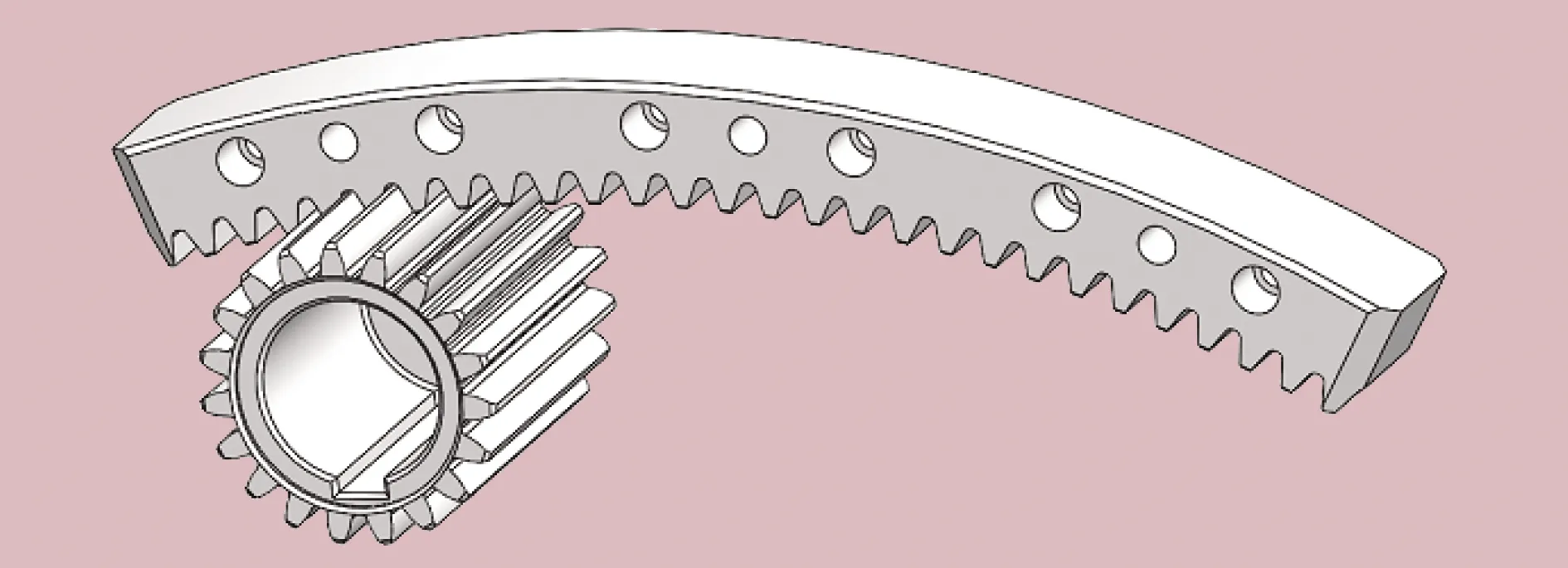
图4 内啮合齿轮副三维模型

对内啮合齿轮副模型进行网格划分,主体采用六面体单元,单元尺寸为3 mm,并对啮合齿轮对廓形面进行细化处理。网格划分后内啮合齿轮副有限元模型如图5所示,共计357 267个单元、706 797个节点。在啮合齿对廓形面之间添加接触,接触类型选择bonded。

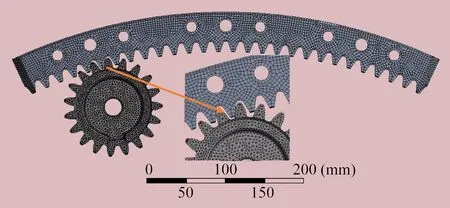
图5 内啮合齿轮副有限元模型

对辐射治疗头在0°～15°摆动范围内的受力状况进行计算分析,考虑不同位置处内啮合齿轮副的受力。当滚筒旋转角度为0°或180°时,辐射治疗头摆动至15°,此时作用在圆弧齿条上的扭矩为6 212 N·m。在驱动小齿轮内孔及键槽两侧施加Fixed Support约束,在圆弧齿条与辐射治疗头安装接合面施加扭矩载荷。最大受力状态下内啮合齿轮副的应力云图如图6所示,最大应力与齿根弯曲应力理论计算值的偏差约为9%。理论计算值选择的计算载荷因数为1.221,考虑实际摆动过程中的冲击作用,仿真分析施加静态载荷,由此造成仿真计算值小于理论计算值。若按理想平稳工况分析,计算载荷因数取1.1,齿根弯曲应力理论计算值为105.82 MPa,与有限元分析的结果106.59 MPa偏差为1%,确认有限元分析结果可信。

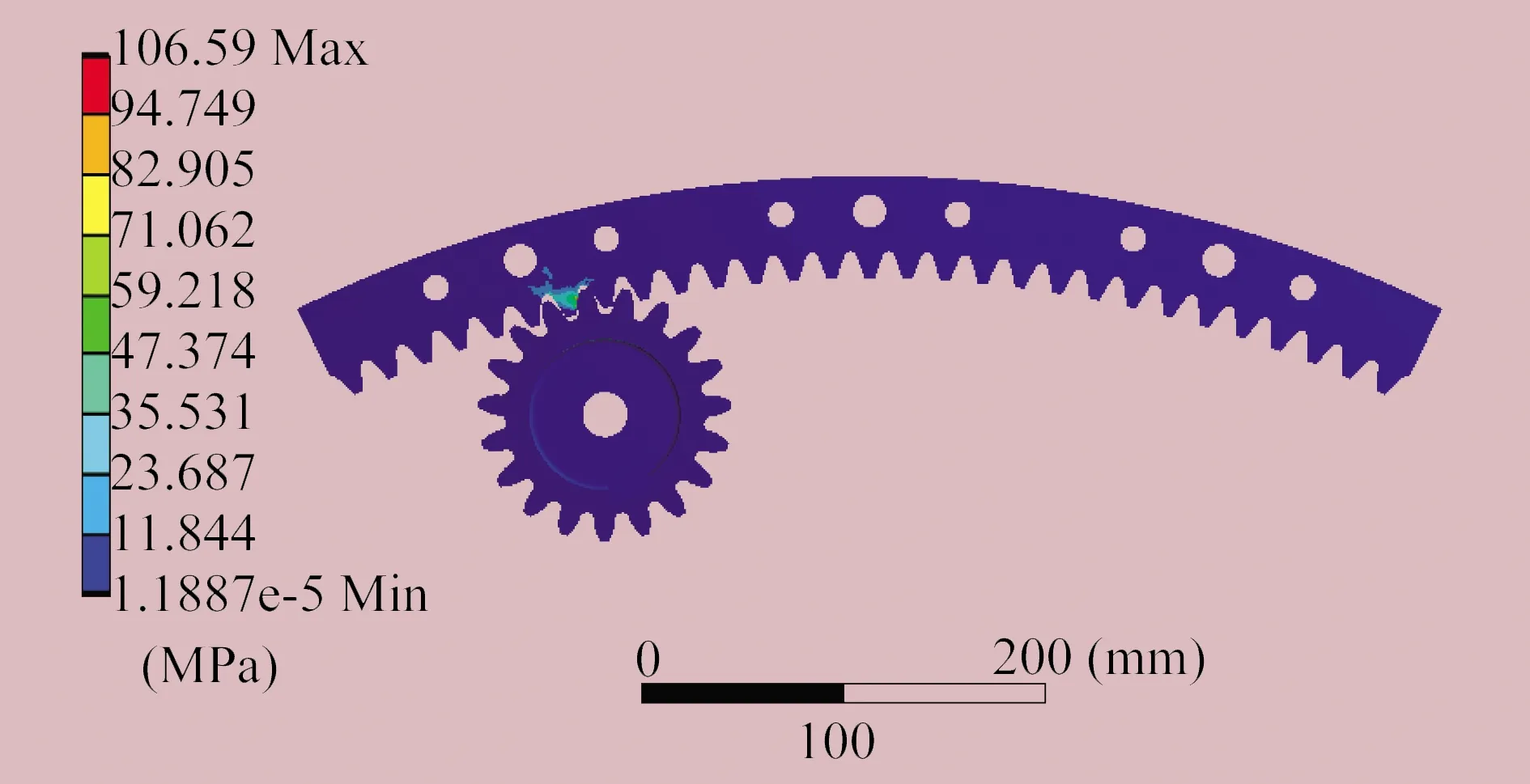
图6 最大受力状态下内啮合齿轮副应力云图

依据医疗设备安全法规要求,辐射治疗头在治疗区上方摆动,属于悬挂物,应在8倍载荷下计算齿轮强度,以保证安全性[10]。按8倍最大扭矩施加载荷,分析内啮合齿轮副的强度,内啮合齿轮副的应力云图如图7所示。此时最大应力值为852.74 MPa,略大于材料的屈服强度(835 MPa),小于材料的弯曲疲劳极限(1 050 MPa),由此可以判断不会出现齿部断裂破坏,满足悬挂物的安全要求。

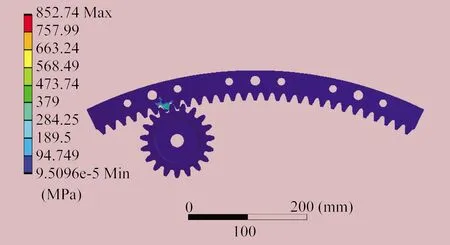
图7 施加8倍载荷时内啮合齿轮副应力云图

6 结束语

笔者基于内啮合齿轮副设计了大型放射治疗设备中的辐射治疗头圆弧提升运动机构,并对内啮合齿轮副中的齿根弯曲应力进行了理论计算及有限元分析。当载荷施加方向发生往复变化时,重载驱动齿轮会产生冲击,主要由齿侧间隙引起,因此需要合理控制齿侧间隙,抑制冲击。齿根弯曲应力的有限元分析结果与理论计算结果为同一数量级,偏差为1%,确认有限元分析结果可信。

通过搭建试验测试平台,实测辐射治疗头摆动过程中驱动电机的电流值,并核算扭矩变化,与理论计算值接近,验证了理论计算与仿真分析数据的真实性,为辐射治疗头进入整机联调提供了保障。