基于防治策略的毒品滥用流行病学模型
刘 风
(1.中央司法警官学院信息管理系,河北保定 071000;2.中央司法警官学院戒毒康复研究中心,河北保定 071000)
0 引言
数学流行病学模型对于预测和控制传染病的流行具有重要实用价值。自从SIR(Susceptible-Infected-Removed)流行病模型出现以来,针对某些流行病患者康复一定时期后免疫力丧失,可能再次被感染的现象,相关学者又先后提出了SIS(Susceptible-Infected-Susceptible)和SIRS(Susceptible-Infected-Recovered-Susceptible)等模型[1-2]。
控制疾病传播的一种常规措施是对患者进行隔离治疗。文献[3-5]考虑隔离治疗措施分别建立了SIQR(Susceptible-Infected-Quarantined-Recovered)和SIQRS(Susceptible-Infected-Quarantined-Recovered-Susceptible)模型,并针对相应的阈值参数讨论了模型的平衡点和稳定性以及一定约束条件下模型的动力学性态。除此以外,通过接种疫苗(vaccination)使易感个体获得免疫力,是防止疾病流行的另外一种有效方式。Parsamanesh等[6]分析了带有疫苗接种措施的SIS模型的全局稳定性;Arino 等[7]针对SIRS 模型研究了疫苗接种措施对模型稳定性的影响,当疫苗并非完全有效时,模型将会出现后向分支。
考虑到毒品滥用与传染病的扩散原理高度相似。White等[8]针对海洛因的流行构建了一个SIR模型,分析了模型平衡点的局部稳定性,并给出了后向分支存在的必要条件。Mulone等[9]对文献[8]进行了补充,证明了其平衡点的全局稳定性。通过对药物使用者依赖程度的划分文献[10]提出了一个双药物使用人群的流行病模型,并对模型进行了定性分析。以上研究成果均假设治愈后的吸毒者具有永久的毒品“免疫力”,针对此问题,文献[11]提出了一个具有暂时“免疫力”的毒品滥用流行病学模型,并分析和证明了模型平衡点的存在性和稳定性。
现实中,由于各种原因,只有有限的吸毒人员能够接受治疗,所以,单纯地依靠治疗手段难以从根本上消除毒品滥用现象的发生。为了更有效地防止毒品滥用的蔓延,针对毒品易感人群加强宣传教育(类似于接种疫苗),提高其自身“免疫力”不失为一种合理的预防措施。虽然上述毒品滥用流行病学模型刻画了事后的治疗手段,但是作为影响毒品滥用关键因素的事前预防措施,却没有被引入到模型当中。而现有带接种疫苗预防措施的流行病学模型均假设患者在接受治疗期间除发生死亡情况外将全部治愈,这又与戒毒人群并非全部能够戒断“毒瘾”,其中一部分戒毒人员结束治疗后仍然未能康复的特点不相符合。因此,以各种传染病为背景的流行病学模型无法直接用于分析研究毒品滥用的传播规律。
鉴于上述原因,本文在文献[11]的基础上,针对其仅考虑了单一治疗措施的不足,引入预防机制,提出了基于防治策略的毒品滥用流行病学模型,定性分析了模型的动力学性态,将模型的基本再生数与文献[11]中单纯依靠治疗措施的基本再生数进行了比较,并经过仿真实验进行了验证,研究结果表明,若非预防措施完全无效,此模型比文献[11]中的模型能够获得更小的基本再生数,采取综合防治策略,通过提高预防措施的效果,可以避免产生后向分支现象,更有效地防止毒品滥用的滋生。
1 模型构建
经过治疗的戒毒人员中,只有部分个体能够治愈,对毒品产生“免疫力”,而这种“免疫力”不是终生的,随着时间的推移,可能逐渐丧失。在考虑上述特点的基础上引入预防机制,将总体人群划分为四类,即易感人群、未隔离吸毒人群、隔离治疗人群和免疫人群,建立了基于防治策略的SITRS(Susceptible-Infected-Treated-Recovered-Susceptible)模型。毒品滥用相关人群的状态转换过程如图1所示。
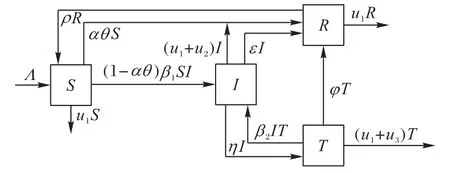
图1 毒品滥用相关人群的状态转换过程Fig.1 State transition process of populations correlated with drug abusers
其中:S、I、T、R、Λ分别代表易感人群、未隔离吸毒人群、隔离治疗人群、免疫人群以及系统补充人群的人数在总体人群中所占的比例。θ为针对易感人群进行毒品危害宣传的覆盖率,α为宣传教育的有效率,假定0 ≤α<1,即宣传教育并非完全有效。u1代表自然死亡率,u2和u3分别为未隔离吸毒人群和隔离治疗人群的吸毒致死率,ε是未隔离吸毒人群的社区治疗康复率,η为隔离治疗率,假设未隔离吸毒人群对易感人群具有传染性,隔离治疗人群不具有传染性。β1是未隔离吸毒人群与易感人群之间的接触传染率,β2是解除隔离治疗人员的复吸率,φ是隔离治疗的康复率,免疫人群的“免疫力”将逐渐丧失,“免疫”丧失率为代表平均“免疫期”。各人群间转换规则如下:
1)预防措施使易感人群中αθ比例获得“免疫力”,进入免疫人群。
2)(1-αθ)比例未获得“免疫力”的易感者以β1I的概率被感染,成为未隔离吸毒者。
3)η比例的未隔离吸毒者会接受隔离治疗,进入隔离治疗人群;社区治疗使ε比例的未隔离吸毒者得以康复,获得“免疫力”,进入免疫人群。
4)φ比例隔离人员治疗后将康复,获得“免疫力”,进入免疫人群;解除隔离人员以β2I的概率重新成为未隔离吸毒者。
5)免疫人群以ρ的概率重新成为易感者。
根据上述转换规则,按照图1建立微分方程模型:

2 平衡点和稳定性分析
按照文献[12]提出的基本再生数的计算方法,系统(5)~(7)的再生数RVT可表示为:
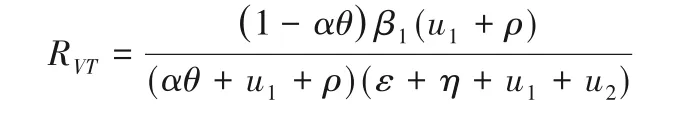
2.1 无毒平衡点及其稳定性

在无毒平衡点E0处,其雅可比矩阵为:
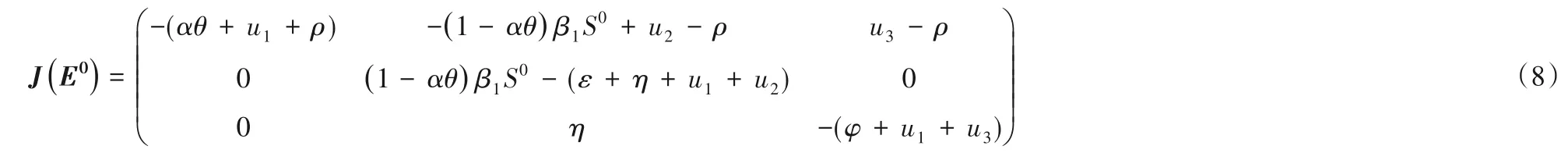

2.2 地方病平衡点及其稳定性
考虑RVT>1时,如果地方病平衡点E*=(S*,I*,T*)存在,则有S*≥0,I*>0和T*≥0使得:

因为当RVT>1 时,无毒平衡点E0不稳定,所以对于系统(5)~(7),除可行域边界上的点以外,从可行域内部出发且充分靠近E0的初值点的解均远离E0。若存在集合K={E0}⊂Γ,则K是一个紧不变集,设KS是K的稳定集,即KS包含了所有ω极限集ω(F)⊂K的初始可行解F,则KS只能存在于可行域的边界上,这意味着可行域边界上的最大紧不变集K是孤立的,由文献[14]中定理4.1可知,系统(5)~(7)是一致持续的。

引理1定理3.5[17]。当单连通的可行域Γ内存在一个紧吸引集K⊂Γ时,若<0,则Γ内的唯一平衡点是全局渐进稳定的。
定理2对于系统(5)~(7),当RVT>1 时,∃ξ1>0 和ξ2>0,若“免疫力”丧失率ρ<min{ξ1,ξ2},则地方病平衡点E*具有全局渐进稳定性。
证明 系统(5)~(7)的可行域Γ是单连通的,且由命题1、命题2 和引理1 可知,证明定理2 成立,需在赋范空间R3中选择一个适当的向量范数|⋅|和一个3×3 的矩阵值函数以保证<0。



2.3 后向分支


若β2η(u1+ρ)2>(ε+η+u1+u2)Z,则a>0,系统(17)~(19)可能出现后向分支现象。
后向分支现象的出现打破了传统意义上将基本再生数作为控制疾病传播的阈值理论,对于毒品滥用问题,这意味着即便RVT<1,除无毒平衡点外,同时还可能有一个稳定的地方病平衡点,毒品滥用现象仍然不能杜绝。只有采取更有效的措施,才能充分降低基本再生数,避免后向分支的产生,防止毒品滥用形成地方病。
考虑基本再生数

3 数值模拟
以某市相关数据为基础设定参数(见表1),其中,自然死亡率u1为2009—2018年该市常住人口的平均死亡率,吸毒致死率u3依据该市2010—2018 年接受隔离治疗的戒毒人员平均死亡率以及自然死亡率u1计算,假定未隔离吸毒致死率u2与u3相同,隔离治疗康复率φ为隔离治疗人员的3 年操守率,“免疫”丧失率ρ根据标准操守期的倒数计算,社区治疗康复率ε、隔离治疗率η和复吸率β2分别根据相关资料按照吸毒人员的显性/隐性比进行调整,宣传覆盖率θ根据十八大以来全国历年在校生人数和累计接受禁毒教育学生人数估计调整。

表1 模型参数设置Tab.1 Parameter settings of model
利用MatLab软件模拟仿真不同初始条件下易感人群、未隔离吸毒人群和隔离治疗人群的演化过程,验证后向分支和各平衡点的存在性及稳定性。
首先,考虑β1取值0.044,即当RVT=0.982 时,如图2 所示,由于初始值不同,导致系统出现不同的平衡点,即同时存在无毒和地方病两个均衡,可以看出,地方病平衡点E*是稳定的,而无毒平衡点E0不稳定,模拟结果支持了后向分支现象出现的可能性。
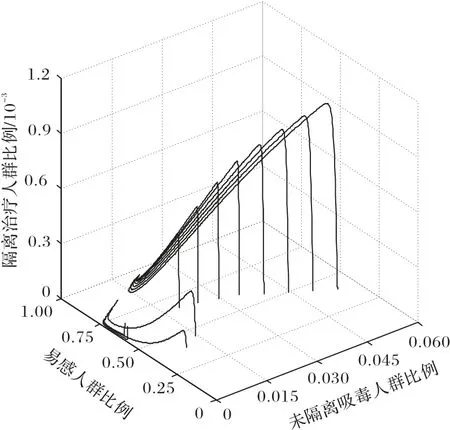
图2 无毒和地方病两个平衡点同时存在(RVT=0.982)Fig.2 Drug-free and endemic equilibrium points exist simultaneously(RVT=0.982)
其次,保持β1不变,假设宣传教育完全无效,即α=0,则RVT=1.158 >1,如图3 所示。对于任意的初始值,解曲线最终都汇聚到唯一的平衡点,仿真结果表明系统唯一的地方病平衡点E*是全局渐进稳定的,单纯依靠治疗措施,难以从根本上杜绝毒品滥用的滋生,终将形成地方病。
最后,β1仍然取值0.044,维持原有的教育有效率α,将宣传覆盖率θ提高到50%,此时RVT=0.300 <1,如图4所示。无论初始状态如何,未隔离吸毒人群和隔离治疗人群的比例最终都将趋近于0,可见,相对于文献[11]中单纯依靠治疗措施,通过综合防治,在教育有效率较高的前提下,提高宣传覆盖率可以避免后向分支的出现,更加有效地消除毒品滥用现象的产生。结合图2 中后向分支现象的出现,模拟结果验证了无毒平衡点E0的存在性和局部渐进稳定性。
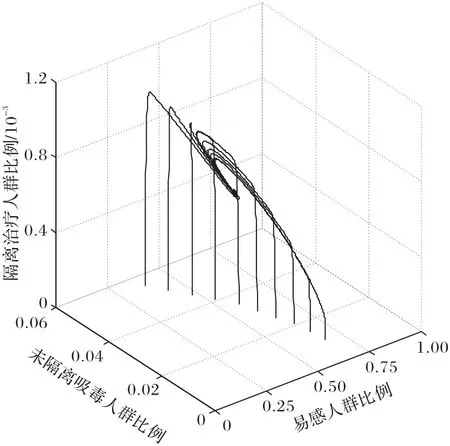
图3 地方病平衡点模拟结果(RVT >1)Fig.3 Simulation results of endemic equilibrium point(RVT >1)
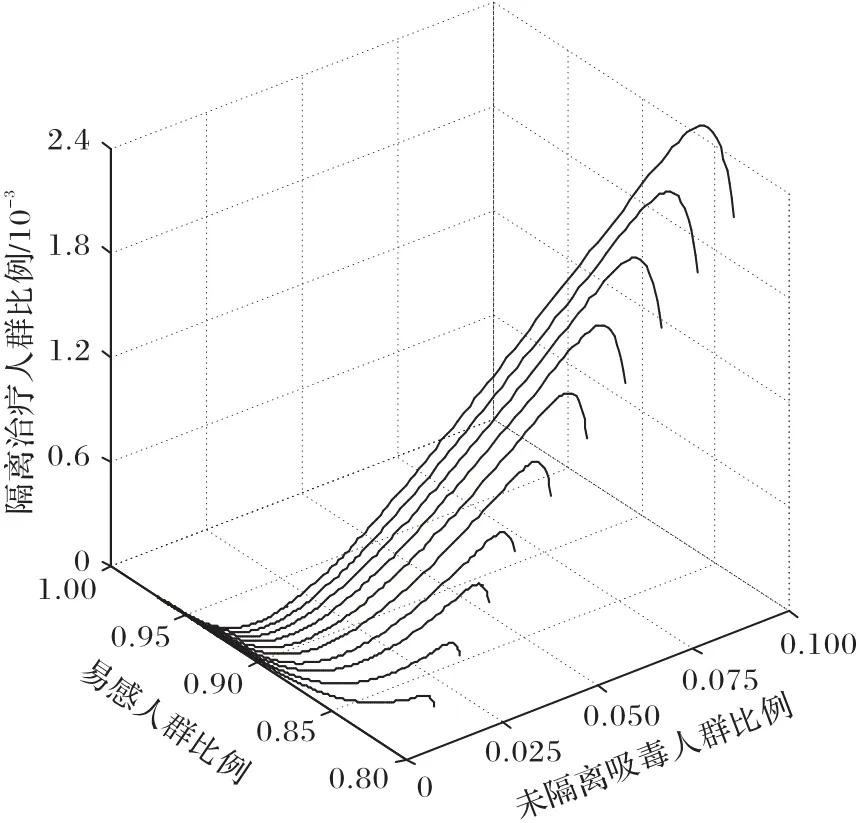
图4 无毒平衡点模拟结果(RVT <1)Fig.4 Simulation results of drug-free equilibrium point(RVT <1)
4 结语
应用流行病学原理研究毒品滥用问题尚处起步阶段,现有研究成果对毒品滥用的预防措施考虑不足,本文通过引入预防机制,构建基于防治策略的毒品滥用流行病学模型,对模型进行了定性分析,并计算了可能存在后向分支的必要条件,比较了单一治疗和综合防治策略下的基本再生数。模拟实验验证了后向分支的存在性和平衡点的稳定性。研究结果表明单纯依靠治疗措施,难以从根本上消除毒品滥用现象,采取综合防治策略,通过提高宣传覆盖率θ和教育有效率α,能够进一步降低文献[11]中的基本再生数,更加有效地防止毒品滥用的滋生。

