基于思辨能力发展的数学开放题课例资源开发

思辨能力是一种高阶思维能力，是为“依据标准，对事物或看法做出一种有目的、有理据的判断的能力”。数学思辨能力是学生数学素养水平的一个重要标志，是小学数学教学不可或缺的一环。

开放题学习能有效发展学生的数学思辨能力，但在小学数学教科书中，现成的开放题数量较少。从这个角度来说，加强开放题课例资源的开发是培养学生思辨能力的迫切要求。小学数学开放题包括条件开放题、结论开放题、策略开放题、综合开放题，对常规题的改造角度有很多，可以对条件或问句进行增减，也可以对习题内隐活动、解题策略进行全局性的优化和建设性的改良，从而使常规题变成开放题，让问题解决过程更具思维张力和学习魅力，让学生从“浅层思考”迈向“深刻思辨”。下面笔者结合常规题改造、后续教学中思辨问题及活动开展，谈谈开放题课例资源的开发和使用。

课例1：条件开放题的资源开发

条件开放题包含条件不全、条件多余和条件隐含等类型，需要学生在观察、类比、分析、联想、抽象和概括等思维过程中抓住有用条件，发现隐含条件，不用或少用干扰条件和多余条件，以便从不同角度寻找解决问题的方法。

【原题】（苏教版数学教材一年级下册第11页）桃树和梨树一共有15棵。

（1）桃树有6棵，梨树有多少棵？

□○□=□（棵）

（2）梨树有9棵，桃树有多少棵？

□○□=□（棵）

【分析】在“桃树和梨树一共有15棵”的前提下，通过具体给出其中一种果树棵数求另一种果树棵数，两小题之间具有桃树6棵、梨树9棵这样的条件和问题之间的互逆特点。此题的改编是减少指定条件，让学生自行假设条件。

【教学指要】本题教学时可以呈现不同指向、不同难度、不同开放度、不同区分度的问题推动学生的思辨。思辨问题一开始可以由教师逐步给出，通过一段时间训练后再由教师启发学生提出。考虑到一年级学生的身心特点，可以具体设计三个层次的问题（括号中文字为思辨要点）。

思辨1：梨树和桃树棵数之间有什么关系？15棵是什么意思？（分析，建立条件和问题相关性）

思辨2：可以先假设哪种果树是多少棵？还可以是多少棵？（假设，有根据地尝试）

思辨3：梨树和桃树的棵数有多少种不同的情况？按照一定顺序写一写。（反思，有条理地列举）

课例2：结论开放题的资源开发

结论开放题就是根据已知条件进行判断，所获得的结论不确定。学生对每一个结论的审视都直接指向对知识本质的理解和对所学内容的批判性利用。

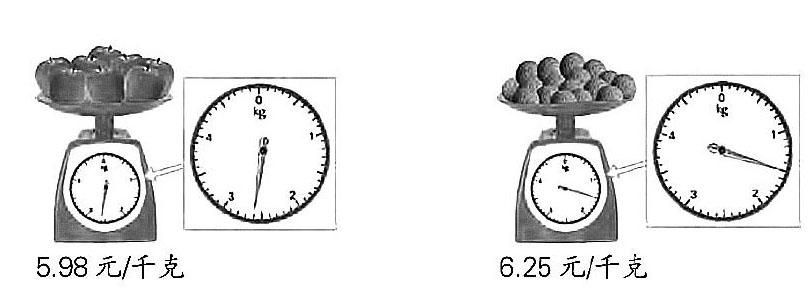
【原题】（苏教版数学教材五年级上册第68页）购买下面的水果各要多少元？（得数保留两位小数）

【分析】数学源于生活，又服务于生活。学习能否真实发生，首先取决于探索问题的真实性。本题思辨点在于如何结算，学生能否想到人民币单位而主动保留两位小数，又能否根据实际支付方式对计算结果保留合适的近似数？

【开放题】李阿姨在超市买散装东北大米。售货员将大米称重后贴上价格标签。已知大米标签上单价：5.98元/千克，质量：3.624千克。付款时李阿姨会付多少钱？

【教学指要】改编后的开放题非常考验学生的思辨能力，结论的多样性来自对生活场景的不同理解，此题的不同结论较为隐蔽。“标多少元”“付多少元”与生活息息相关，是两个有联系又有区别的问题。首先是人民币的单位和实际流通情况，标签总价是21.67元，现金支付时受硬币流通影响，则不会精确到分，实付21.6或21.7元（这里不考虑菜市场中随机让利和讨价还价情况所带来的其他付款可能）;其次是考虑付款方式对结论的影响，用支付宝、微信、刷卡时一般扣除21.67元。习题使用时，可以围绕三个思辨方面拾级而上，探索和经历实际问题解决的过程。

思辨1：标签上的总价会是5.98×3.624的乘积吗？总价为什么保留两位小数（21.67元）？（联系，总价保留两位小数）

思辨2：会直接付21.67元吗？如果付30元，怎样找零？（质疑，付款和找零中的数学现实）

思辨3：有其他付款方式吗？各付多少元？需要找零吗？（反思，多种付款方式）

课例3：策略开放题的资源开发

一题多解，是策略开放题的显著特征。从一种解题策略到多种解题策略，学生在变换思维角度、调用不同知识储备时，思辨能力必定全面提升。

【原题】（苏教版数学教材五年级下册第74页）写出一个比[15]大又比[14]小的分数，并互相说说自己是怎样想到这个分数的。你还能再写出几个这样的分数吗？

【分析】此题是苏教版教科书中呈现的典型开放题，答案不唯一，解题策略有多种。如果仅关注答案多样，习题中蕴含的思维灵活性和深刻性就得不到较好的体现。教学时教师可从重点策略上着手，组织学生思辨。“先通分，再比较每组分数的大小”是学生之前接触最多的题型。通分是学生的首选，要找到更多的中间分数，学生一般会用更大的数作为分母。一再调整分母时，学生的苦恼随之而来。

【教学指要】思辨就是通过一定的标准评价思维进而改善思维。本题教学时如果时间允许，可以“小题大做”，安排一整节课来让学生充分感受，获得更加开放、自信的思辨情感。学生先独立思考，接着合作交流，然后教师引导，最后回顾反思。学生思考和教师引导可围绕以下三个思辨问题。

思辨1：使用通分的方法，找一个或找多个中间分数，分母为什么要变化？（分析，方法的局限性）

思辨2：还有没有其他方法？[14.1]可以吗？化成小數可以吗？还有没有其他方法？（比较，方法的灵活性）

思辨3：不同方法之间有什么联系？你喜欢哪种方法？（沟通，方法的逻辑性）

此题常用解决策略有同分母、同分子、化小数等。

方法一：化成同分母，即通分。

方法二：化成同分子。[15=1050]，[14=1040]，根据同分子分数的大小比较方法，符合要求的分数有[1049]，[1048]，[1047]，…[1041]。

方法三：化成小数。[15=0.2，][14=0.25，]大于0.2而小于0.25的小数有无数个，写出几个小数后再分别化成分数。[0.21=21100，][0.211=2111000]等。

课例4：综合开放题的资源开发

综合开放题，通常只给出一定的情境，其条件、解题策略与结论都需要在情境中自行设定与寻找。比如，皮球在倾斜的木板上能滚多远？怎样测量一个石头的体积？学校一天的垃圾有多少？综合开放题具有明显的实践性。

【原题】（苏教版数学教材四年级下册19页）读出横线上的数：2010年第六次全国人口普查显示，我国人口总数大约是1 339 720 000人，其中，少数民族人口总数大约是113 790 000人。

【分析】此题信息主体是第六次全国人口普查。全国人口普查属于国情国力调查，是提供全国基本人口数据的主要来源。在普查标准时点上采集的人口数据是准确数，也是唯一数，而在实际生活情境中，根据不同的对话群体，所使用的近似数是不同的。这就是生活的数学化和数学的生活化。题中全国人口总数和少数民族人口总数均为整万的近似数。人口普查数据是最真实、最直接、最权威的多位数，用好这一素材，可以统摄整个单元教学。

【开放题】从报纸、书籍或网上收集第六次全国人口普查数据，选择一些数据与同学交流。

【教学指要】本题最佳的打开方式是实践活动。基于问题设计活动，基于活动解决问题，学生可以立足以下三个层面思考和辨析。

思辨1：什么是人口普查？第六次全国人口普查是什么时候？普查哪些内容？第六次人口普查全国总人口是多少？（关注，了解活动意义）

思辨2：从哪里获得权威的人口数据？世界各国（洲）人口情况是怎样的？（阐述，掌握有效数据获取途径）

思辨3：怎样根据生活情境去选择合适的总人口近似数？为什么不使用精确数？（评价，表达上善解人意）

具体来说，教师设计及落实的活动依次有以下几方面。

讲一讲：什么是人口普查？建议采用小学生数学微演讲的方式。

查一查：第六次人口普查数据是多少？全体学生分小组查找资料，推荐访问国家统计局官网。

听一听：教师播放《新闻联播》中第六次人口普查数据公报的视频，让学生了解大数的读法。

读一读：读出自己感興趣的一些数据。

比一比：呈现媒体上大数的真实材料，了解四位一级和三位一节的大数读写方法。

说一说：根据生活场景的不同，说出各种统计量不同的近似数，大约是多少万、多少亿。了解数据的无法精确和没必要精确。

做一做：制作一份数学手抄报，罗列第六次人口普查各种数据。

估一估：第七次全国人口普查将于2020年11月1日0时开展。通过估计，保持对人口普查数据持久的关注和敏感。

在素养为本的教学下，数学开放题的设计要考虑如何提升学生的推理能力和数学思维能力，还要考虑如何促进学生的合作交流能力。将常规题开发成开放题，教师要吃透原题，尊重原题，多角度解读习题素材的内在价值，找准习题的生长点、支撑点和延伸点，不能为开发而开发。

（作者单位：江苏省昆山市玉峰实验学校）

参考文献

[1]文秋芳.中国外语类大学生思辨能力现状研究[M].北京：外语教学与研究出版社，2012.

[2]杨传冈.小学数学几何开放题的思维评价[J].教学与管理（小学版），2018（5）：29-31.

[3]张侨平，唐彩斌.落实素养为本的数学开放题教学[J].数学教育学报，2019（6）：61-64.

[4]仲崇恒.小学高年级数学习题资源的开发和使用[J].现代中小学教育.2014（5）：35-38.