BL Lac天体喷流物理参数的限定∗

方 雪 伍 林 毛慰明 康世举 郑永刚

(1 云南师范大学物理与电子信息学院昆明650500)(2 六盘水师范学院物理与电气工程学院六盘水553004)

1 引言

通常认为射电噪活动星系核(Active Galactic Nucleus, AGN)中都有喷流的存在, 耀变体(Blazar)作为AGN中最活跃的子类, 其观测特征为[1–2]: 高光度, 快速大幅光变, 高偏振, 视超光速运动, 喷流与观测视线夹角很小, 非热连续谱等. 耀变体根据光谱分为[3]:具有很弱或没有发射线的蝎虎天体(BL Lac object, BL Lac)和具有宽发射线的平谱射电类星体(Flat Spectrum Radio Quasar, FSRQ). Blazar多波段的长期观测可以提供源在不同态时的宽波段能谱分布; 而对多波段的能谱分布的研究可以为相对论喷流运动提供重要信息.

由磁化等离子体组成的耀变体喷流从中央超大质量黑洞附近几乎沿着观测者方向以相对论速度射出[4]. 喷流内的相对论粒子产生非热连续辐射, 其辐射谱覆盖了从射电波段到伽马射线波段的整个电磁波谱, 且能谱分布(Spectral Energy Distribution, SED)特征在整体上呈现明显的双峰结构(在lgν-lgνFν图上,ν为频率,νFν为某频率处的能流). 目前, 轻子模型和强子模型被用于解释BL Lac天体的SED双峰结构. 在轻子模型中,低能峰主要来自于喷流内相对论电子的同步辐射, 高能峰主要来自于极端相对论电子的逆康普顿散射. 根据逆康普顿散射(Inverse Compton, IC)的种子光子的来源不同, 轻子模型可分为外康普顿模型(External Compton, EC)[5]和同步自康普顿模型(Synchrotron Self Compton, SSC)[6–7]. 与轻子模型相比, 强子模型认为高能辐射起源于极端相对论质子的级联过程[8–9]或者质子同步辐射过程[10].

对于BL Lac天体非均匀锥形喷流模型参数的限定, 柴博和曹新武已经做了相关研究[11–12], 而我们采用均匀SSC模型对BL Lac天体进行研究. 在轻子辐射起源模型中, 一般根据观测到的电磁辐射能谱的谱形假设一个非热电子谱分布, 该相对论性电子群通过同步辐射和逆康普顿散射过程产生观测到的电磁辐射能谱[13–15]. 上述能谱拟合过程涉及各个模型参数数值的调整. 由于模型参数范围不确定而导致参数自由度太大, 能谱拟合效率低. 本文以双幂律电子谱为例, 利用多波段观测数据对BL Lac天体谱的物理参数进行计算, 得出了相关参数限定结果, 并用Mrk 421、Mrk 501天体的准同时性多波段数据进行了验证. 该限定方法能提高耀变体多波段能谱拟合过程中的参数数值调整效率. 文中取哈勃常量H0= 70 km·s−1·Mpc−1, 物质能量密度ΩM= 0.27, 辐射能量密度Ωγ=0, 无量纲宇宙学常数Ω∧=0.73.

2 SSC模型

同步自康普顿模型认为低能峰是喷流内极端相对论电子在磁场中受洛伦兹力作用的同步辐射过程产生, 高能峰是同步辐射产生的软光子与相对论电子的逆康普顿散射产生的. 关于模型的详细解释见文献[1, 16–18], 在此仅对该模型进行简单描述.

在均匀同步自康普顿辐射模型中, 假设存在一个充满极端相对论性电子半径为R的球形辐射区, 辐射区内存在一个均匀的随机起源的磁场, 磁场强度大小为B, 辐射区以相对论速度运动, 且观测到的辐射区域受多普勒效应影响, 多普勒因子为:

其中: Γ为体洛伦兹因子,β为喷流速度与光速的比值,θ为观测角.

我们假设喷流内相对论电子谱为一个拐折的双幂律分布:

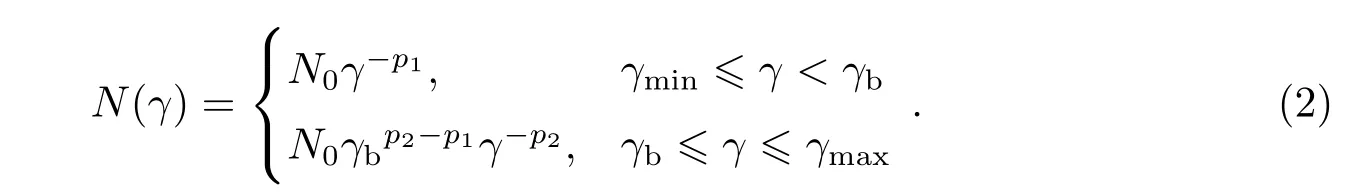
其中,N(γ)为电子谱分布,γ为洛伦兹因子,N0为电子数密度的归一化系数,p1、p2分别为低于和高于拐折能量γbmec2能量段的电子谱指数,me为电子质量,c为光速,γb为电子谱的拐折洛伦兹因子,γmin和γmax分别为电子的最小和最大洛伦兹因子.

在同步自康普顿辐射模型中共涉及9个模型参数, 下面我们对这9个参数(p1、p2、N0、γmin、γmax、γb、B、δ、R)进行讨论.

3 参数的限定

上述SSC模型描述中涉及了9个模型参数, 其中6个参数描述了电子能谱分布(p1、p2、N0、γmin、γb、γmax), 3个参数描述了辐射区域的性质(B、δ、R). 由于电子最大洛伦兹因子对模型影响不大, 我们没有对γmax进行限定, 在文中取γmax=100γb[19], 下面将分别对这两部分进行限定.

3.1 电子能谱参数的限定

3.1.1 电子谱指数的限定

观测上耀变体的多波段SED呈双峰结构,νp为峰值频率,a1、a2分别为低峰频和高峰频的光子谱指数,F0为峰频处的流量, 相对论粒子的辐射谱用一个拐折的幂律谱(ν −νFν)[20]表示:

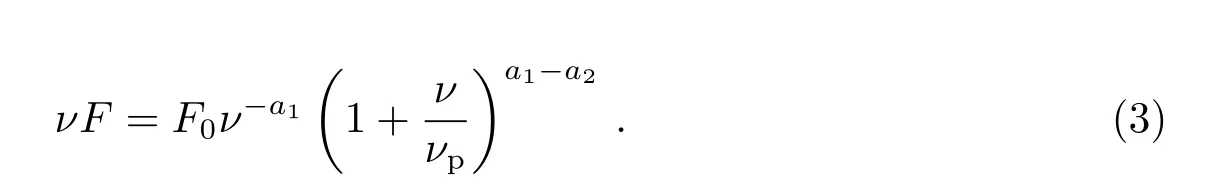
(3)式通过近似计算, 可以得到

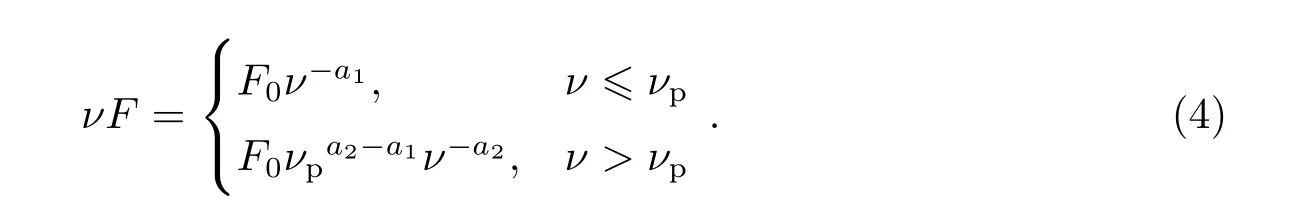
其中,F为某频率处的流量, 流量即在某频率处单位时间辐射的光子数. 同时我们使用一个拐折的幂律谱对能谱进行拟合, 这种方式出现在具体的能谱计算中, 依据为[21]: (1)每个峰值两侧大致呈现幂律分布; (2)单波段的数据表明能谱为幂律; (3)一定的粒子加速演化机制可产生对应的电子谱.

电子谱分布会影响软光子场能量密度(Uph), 致使电子能谱的演化方程是一个积分微分方程. 对于均匀球辐射区的稳态谱, 有恒定电子谱N(γ), 若不考虑光穿越对辐射场的影响, 则在半径为R、发射系数为j(ν)、吸收系数为k(ν)、光深为τ=k(ν)R的均匀球形辐射区域中, 平均单色能量密度为:

其辐射区的光度为:

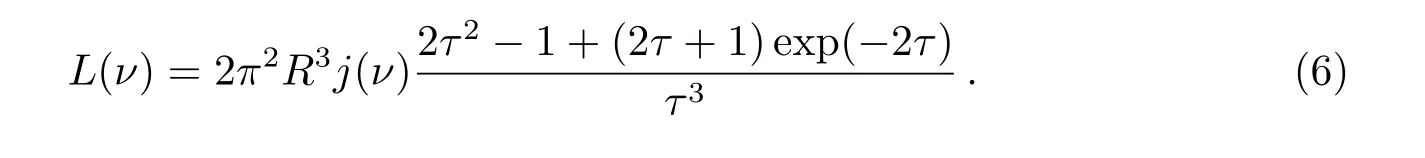
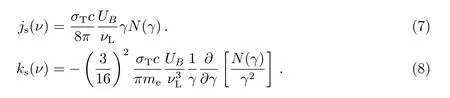
其中:e为单个电子的电荷量为磁场能量密度,me为电子静止质量,σT=6.652×10−25cm2为汤姆逊散射截面.

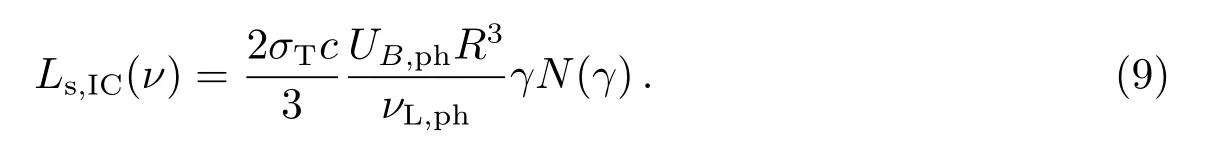
其中:νph为外光子场频率,νs为同步辐射峰值频率,Uph为外光子场能量密度,Us为同步辐射光子能量密度,Ls为同步辐射光度,Ls,IC(ν)为SSC主导IC辐射时的同步辐射光度,UB,ph为外光子场的磁场能量密度,νL,ph为在单色近似条件下外场光子的频率.

若采用拐折的双幂律电子谱来描述相对论粒子谱能量分布, 可得(2)式. 由(2)、(4)、(9)式得[22–23]:

其中:p1,2表示p1、p2,a1,2表示a1、a2.

3.1.2 电子谱拐折洛伦兹因子及电子的最小洛伦兹因子的限定

由多波段准同时性的SED可以得到: 同步辐射峰和逆康普顿辐射峰的峰值频率和峰值光度分别为νs、νc、Ls(νs)和Lc(νc). 对于单区, 均匀的球形辐射区, 其中同步辐射峰值频率为:

其中:νB= 2.8×106B(Hz)为磁场特征频率,Z为红移. 若逆康普顿散射峰值频率在汤姆逊极限下, 有:

由(12)式可知:

若逆康普顿散射峰值频率在Klein-Nishina (KN)极限下, 有:

其中:h为普朗克常数. 由(14)式可知:

只考虑电子加速缓慢冷却情况, 激波加速后, 其谱能分布变为幂律谱[24]:

其中,n(γe)、γe分别为共动系电子数密度和洛伦兹因子,C为电子归一化系数,p为谱指数. 若γmax≫γmin,p>2, 则可以得出电子数密度ne与电子能量密度ee分别为:

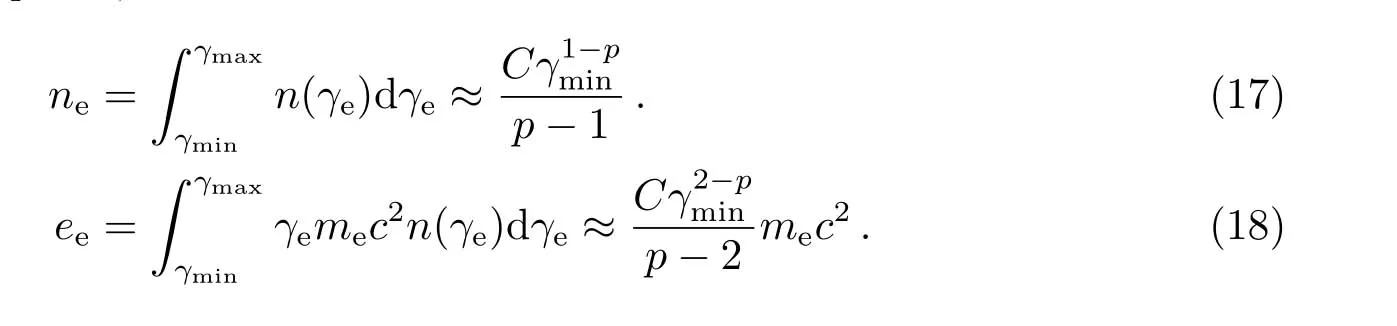
根据激波跃变条件, 电子共动系总内能为:

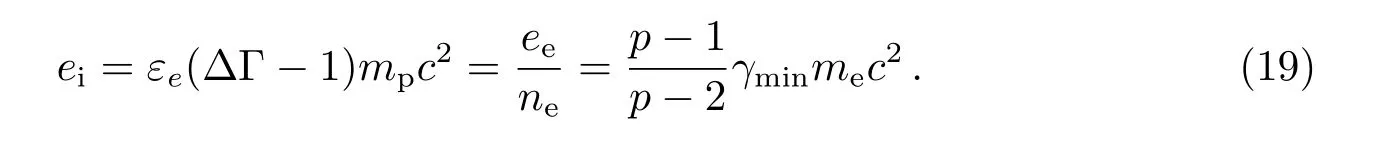
其中,εe为激波的能量转化为电子能量的比例, ∆Γ(∆Γ≫1)为激波相对介质的洛伦兹因子,mp为质子质量, 有[25]:

对于耀变体∆Γ≈1,εe=1; 对于p的取值, 从理论上Sari等人得到典型值[26]:p=2.5.

3.1.3 电子密度的归一化系数的限定

在3.1.1节的讨论中, 已知相对论电子同步辐射, 考虑到多普勒效应后, 其峰值频率和峰频处的光度为[20]:

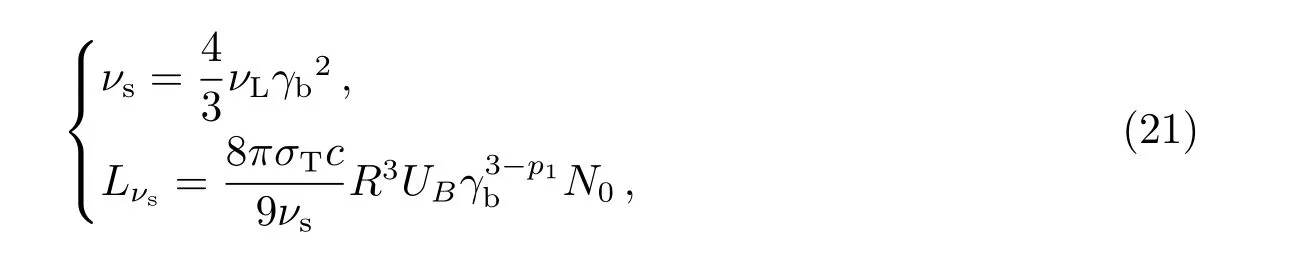
而逆康普顿散射在汤姆逊极限中, 其峰值频率和峰频处的光度为:

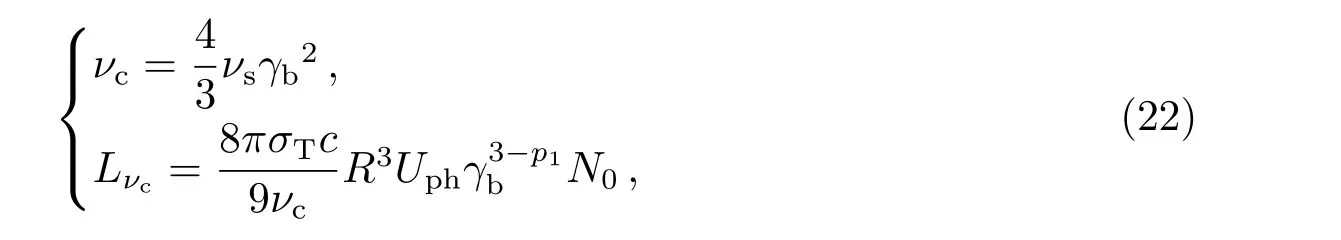
对(4)式积分有Ls,IC=f12νs,ICLνs,IC,f12= 1/(1−a1)+1/(a2−1), 如果SSC主导IC辐射, 有νph=νs,Uph=Us=Ls/(R24πc), 联立(21)、(22)式可得[21]:

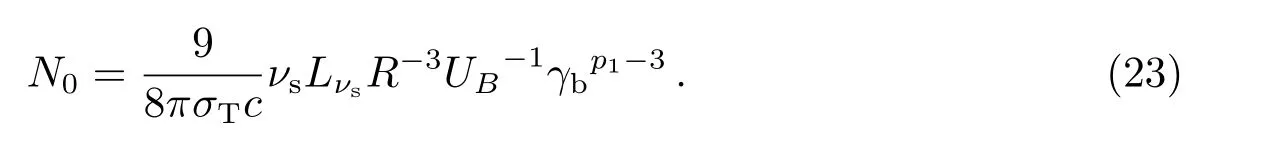
其中,νs,IC为SSC在IC主导时的同步辐射频率,Lνs,IC为SSC在IC主导时的同步辐射光度.

3.2 辐射区域参数的限定

3.2.1 辐射区域半径的限定

在AGN中, 光变时标tobs的定义有多种[27–28], 其一般定义为:

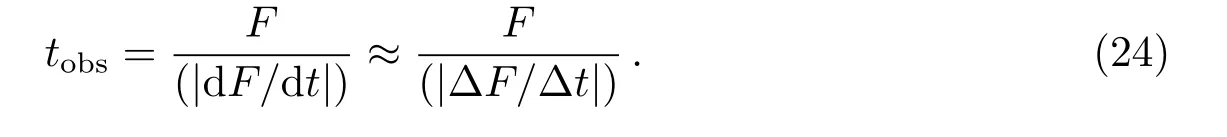
其中, dF/dt是流量随时间变化的快慢程度, 用某一段观测时间内的平均值∆F/∆t来近似, 此方法定义的光变时标为“二倍时间”, 即流量增大到两倍(∆F=F)所需要的时间∆t[29–30], ∆F为流量的增量. 光变时标的保守定义为[31]:

该定义在微分形式上与一般定义等价, 这样的定义对于用星等为单位的观测很方便(∆lnF与星等差相联系).

最小光变时标(∆tobs)满足的条件有[32]: (1)对应的流量变化率为(2)变化的振幅必须大于5σ(σ为单个观测时的标准误差). 一般认为, 耀变体辐射是由相对论喷流主导的[33], 并且产生相对论喷流的辐射, 因为宇宙学红移和多普勒红移影响其光变时标, 需要对所测的光变时标进行宇宙学红移修正和多普勒效应修正, 所以在AGN的静止参考系中的修正时标t0为:

假定在喷流中辐射是各向同性的, 则有: 光变时标不小于光子穿过辐射区域所需要的时间, 所以辐射区域限定为:

辐射产生相对论性喷流, 对(26)、(27)式做多普勒修正后辐射区域大小R′为[34–35]:

3.2.2 辐射区域磁场强度与多普勒因子的限定

由(11)、(13)式可得:

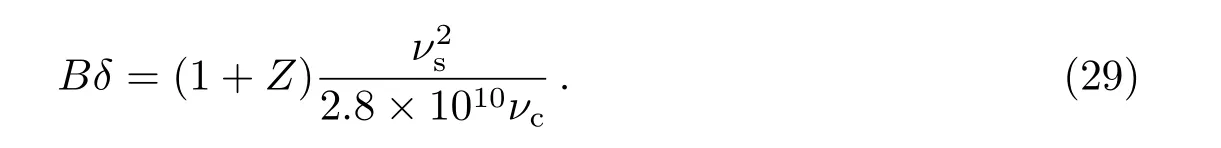
由(29)式可知, 当νs和νc确定时,B和δ成反比. 在同步自康普顿辐射过程中, 同步辐射和逆康普顿散射总光度比值为:

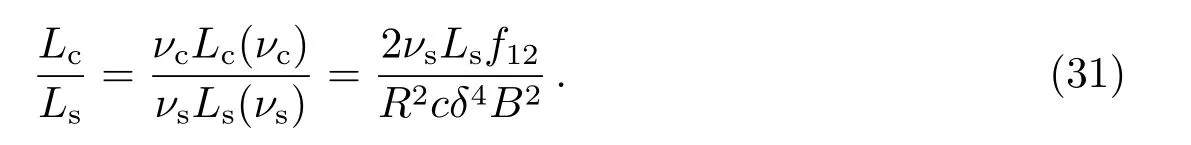
根据(22)、(23)式有:

由(29)、(32)式可得多普勒因子δ为:

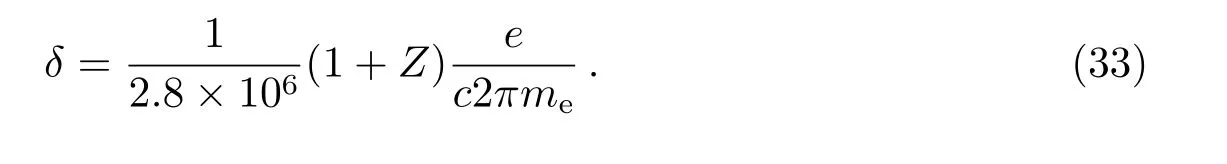
4 参数计算和能谱拟合

在3.1和3.2节的讨论中, 我们限定了SSC模型涉及到的8个参数, 为了验证模型参数限定的合理性,我们把模型运用于Mrk 421、Mrk 501两个天体上. Mrk 421是典型高峰频BL Lac天体. 多波段观测表明Mrk 421在2010年处于活跃期. MAGIC (The Major Atmospheric Gamma-ray Imaging Cherenkov), VERITAS (The Very Energetic Radiation Imaging Telescope Array System), Whipple (The Whipple 10-mγ-ray telescope),Fermi-LAT (The Fermi Large Area Telescope), MAXI (Monitor of All-sky X-ray Image), RXTE (The Rossi X-ray Timing Explorer), Swift (The Swift X-ray Telescope),GASP-WEBT (the GLAST-AGILE Support Program within the Whole Earth Blazar Telescope)和几个光学、射电的望远镜在2010年3月10日到3月22日(MJD 55265–MJD 55277)期间进行了多波段观测. 本文选取该天体在观测期间其中一天(MJD 55268)的多波段数据[36].

同时, BL Lac天体Mrk 501属于第2个被证实为具有甚高能伽马射线辐射的河外天体. 在1998—1999年期间, 其平均甚高能伽马射线流下降了一个量级, 整个甚高能伽马射线能谱分布明显变软. 在2005年、2009年、2012年、2014年都表现出强烈的耀发行为,本文选择Mrk 501天体在2009年3月到8月的多波段观测数据[37–38].

表1中列出了限定Mrk 421和Mrk 501两个天体所需要的观测量, 数据来自于文献[20]; 由(10)、(15)、(20)、(23)、(27)、(31)、(32)式及表1所给数据, 我们计算出相关物理参数值和参数限定结果列在表2中. 利用拐折幂律谱情况下的SSC模型, 我们选取合适的模型参数计算了Mrk 421与Mrk 501的多波段能谱, 并与其准同时性多波段数据进行比对, 结果如图1和图2所示, 计算选取的模型参数值列在表2中.

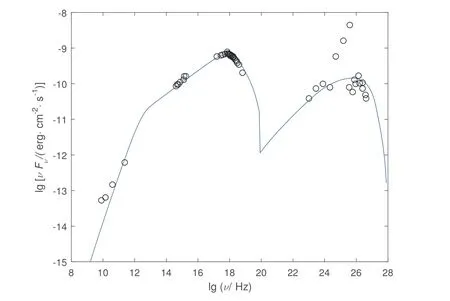
图1 Mrk 421天体多波段能谱分布. 圆圈为多波段的观测结果[36], 实线为模型拟合结果, 结果如下: p1 = 2.34,p2 = 4.50, γmin = 1000, γb = 7.50×105, N0 = 0.50×104, R = 5.20×1016 cm, B = 0.028 Gs, δ = 21.Fig.1 The multi-wavelength SED of Mrk 421. The circles are the multi-wavelength observational data[36]. The line is the results of model fitting. The results are as follows: p1 = 2.34, p2 = 4.50,γmin = 1000, γb = 7.50×105, N0 = 0.50×104, R = 5.20×1016 cm, B = 0.028 Gs, δ = 21.

表1 Mrk 421和Mrk 501的观测量Table 1 The observational quantities of Mrk 421 and Mrk 501

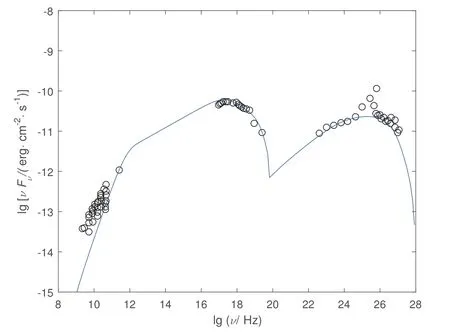
图2 Mrk 501天体多波段能谱分布. 圆圈为多波段的观测结果[37, 39], 实线为模型拟合结果, 结果如下: p1 = 2.50,p2 = 3.50, γmin = 950, γb = 6×105, N0 = 1.30×104, R = 11.30×1016 cm, B = 0.01 Gs, δ = 15.Fig.2 The multi-wavelength SED of Mrk 501. The circles are the multi-wavelength observational data[37, 39]. The line is the results of model fitting. The results are as follows: p1 = 2.50, p2 = 3.50,γmin = 950, γb = 6×105, N0 = 1.30×104, R = 11.30×1016 cm, B = 0.01 Gs, δ = 15.

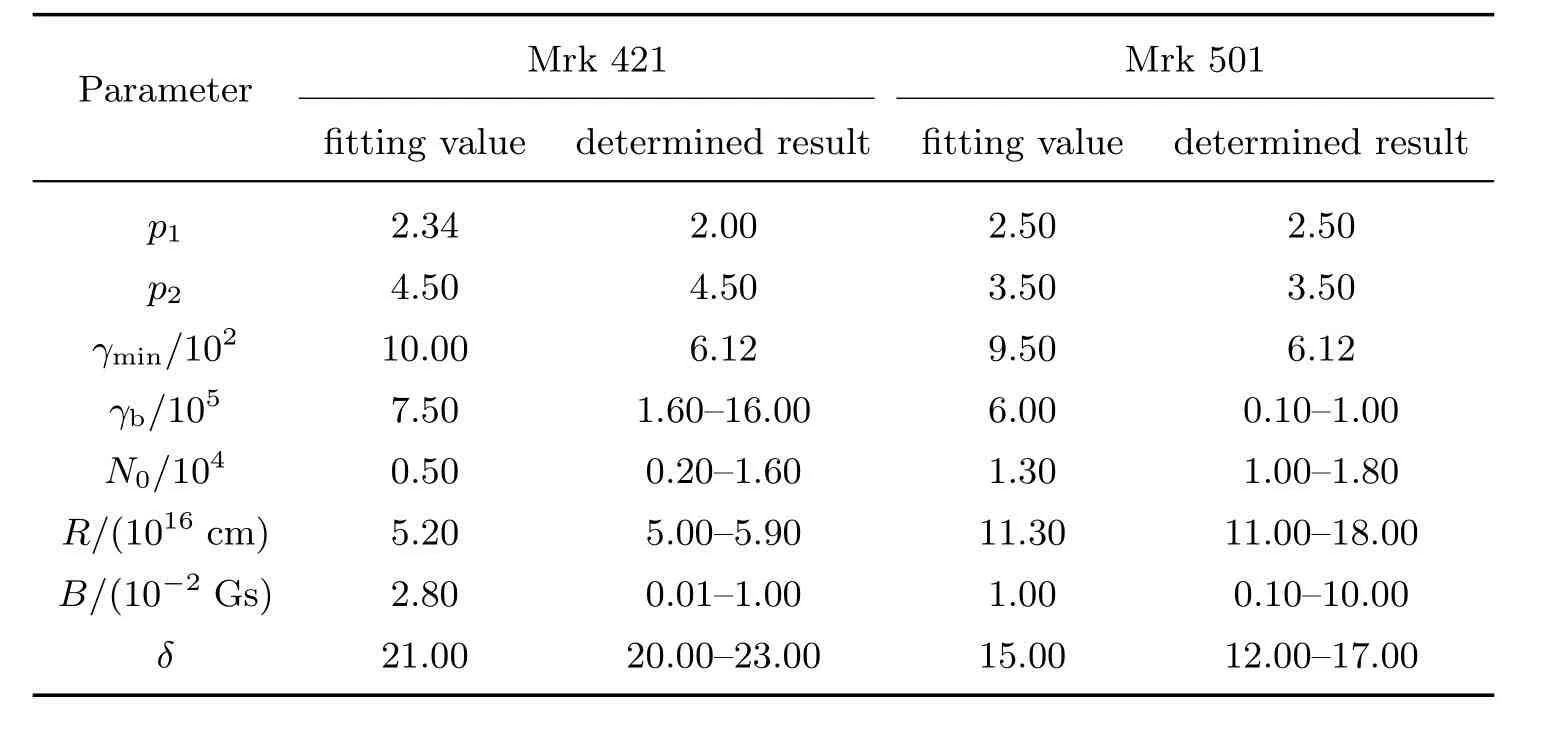
表2 Mrk 421和Mrk 501天体模型选取的参数值和参数限定结果的比较Table 2 Comparison of the model selected parameter values with the determined parameter results of Mrk 421 and Mrk 501

5 总结

通过收集Mrk 421与Mrk 501两个天体的多波段准同时性数据, 我们通过其观测量(表1)计算出参数限定范围, 我们选取合适的模型参数计算了两个源的多波段能谱, 发现在8个模型参数限定的范围内, 我们选取的模型参数值计算出的理论光子谱与两个BL Lac天体的多波段准同时性观测数据符合较好(如图1和图2所示). 但是从图1和图2看出,高能峰有明显的上突, 这是费米能区能量上限(在文献[36]中提到).

表2是模型选取的参数值与参数限定结果的比较. 从表2中可以看出, Mrk 421辐射区域性质的3个参数(B、δ、R), 模型选取的参数值都与限定结果一致; 电子能谱的5个参数, 有4个参数(p1、p2、N0、γb)的模型选取的参数值与限定结果一致, 而电子的最小洛伦兹因子γmin的模型参数值比限定值大; 比较Mrk 501天体的模型选取的参数值和参数限定结果, 其他参数的模型选取的参数值都与限定结果一致, 同样只有电子的最小洛伦兹因子的模型选取的参数值比限定值大. 对于电子的最小洛伦兹因子, 由于电子同步自吸收效应, 最小能量电子的同步辐射无法观测, 以致于我们在限定过程中电子的最小洛伦兹因子出现偏差. 有效的限定电子最小能量的方法是观测其逆康普散射的低能部分能谱, 文献[25]通过LSP (Low-Synchrotron-Peaked)耀变体软X射线的数据限定了电子的最小洛伦兹因子(范围是5–160, 中值为55); 文献[40]也通过拟合FSRQ的SED限定电子最小洛伦兹因子的典型值为48. 但是软X射线能段观测数据很少, 所以很难对这个量给出限定.