LAMOST-Kepler视场中富锂巨星表面转动研究∗

杜明昊 毕少兰 施建荣 闫宏亮

(1 北京师范大学天文系北京100875)(2 中国科学院国家天文台北京100101)

(3 中国科学院大学天文与空间科学学院北京100049)

1 引言

锂元素是宇宙大爆炸形成的4种轻元素之一[1–3], 在天体物理研究中占有重要地位.由于其会在较低温度下(∼106K)发生核聚变反应而消耗, 所以锂元素对于研究恒星内部核反应过程尤为关键. 根据Iben[4]标准恒星演化模型中的描述, 在恒星演化过程的第1次上翻(FDU)过程中, 恒星表面的锂元素由对流运动带到对流层底部并被强烈消耗. 根据恒星模型计算, 一个初始质量1.4M⊙, 金属丰度为太阳金属丰度且初始锂丰度A(Li)=3.3 dex(此处A(Li)=lg(nLi/nH)+12,nLi和nH分别为Li和H元素的数密度)的主序星, 由于第1次上翻过程, 其锂丰度会下降到低于1.5 dex[5]. 然而在长期的观测研究中, 发现大约1%的巨星A(Li)>1.5 dex[6], 称为富锂巨星[7]. 经过数十年的努力, 包括额外混合[8–10]以及外部污染[11–13]的多种学说被提出来解释富锂巨星的形成机制, 然而这种极端天体产生的机制依旧有待确认.

Kepler卫星是由美国国家航空航天局(NASA)设计并发射的科学卫星, 其最初的科学目标为利用凌星法搜寻类地行星. 而凌星法所带来的长时序、连续性的高精度测光观测也极大促进了如星震学、自传测年法等其他恒星物理的研究[14]. 对于每颗观测源,Kepler卫星观测最长时间为从Q0到Q17, 跨度为从2009年5月2日到2013年5月11日的1470 d.Kepler卫星具有两种观测模式: 长段观测(LC)及短段观测(SC). 前者的曝光时间约为30 min, 后者的曝光时间约为1 min, 可用来进行不同的研究任务. 恒星上黑子的存在会导致恒星光度下降, 而由于恒星的自转, 导致观测到的恒星亮度发生周期变化,这种现象被称作自转调制[15–19], 因此利用Kepler卫星光变曲线观测到的恒星自转调制现象进行恒星表面转动研究为研究恒星转动提供了大量样本[20–21].

郭守敬望远镜(LAMOST)是中国最大口径的低分辨率大视场多目标巡天望远镜[22–23], 因为其观测波长范围包含670.7 nm的锂共振线, 所以其百万级别的光谱样本对于利用LAMOST望远镜搜寻富锂巨星具有重要意义. 与此同时, LAMOST提供了较为精确的恒星大气参数. LAMOST-Kepler计划观测了Kepler视场内的恒星[24], 使得将Kepler视场中恒星的光谱观测和光度观测结合起来进行研究成为可能.

在长期的观测中, 富锂巨星的一些特点被发现. 一是富锂巨星在赫罗图上的分布特点. 早期的观测发现富锂巨星在红团簇和水平支附近聚集[25], 但是后来的更多观测发现富锂巨星可以在红巨星支(RGB)的各个位置[26–28]. 虽然现在LAMOST提供的富锂巨星样本较大, 但是与之对应的演化阶段并不好确定, 需要未来更多的观测数据限制. 转动也是富锂巨星的一个重要参数. 由光谱数据得到的投影转动速度(vsini, 其中v为恒星赤道转动速度,i为观测倾角)被发现与巨星锂丰度具有相关性, 高转速的恒星拥有高的锂丰度, 而低转速恒星的锂丰度具有较大的弥散[29–30]. 恒星自转作为额外混合的主要机制已经被大量讨论了[31–33], 尽管其中准确的物理过程还不明确, 如果额外混合确实由转动导致, 那么恒星自旋角速度(Ω)的增加可以增强额外扩散(Dmix)并导致锂增丰[9]. 因为在角动量传输模型中, 作为一级近似,Dmix∝Ω2[34].

尽管富锂巨星与转动的关系已在早期的研究中依靠vsini得到, 本文首次利用Kepler卫星提供的光变曲线LC研究了由LAMOST望远镜搜寻出的富锂巨星的表面转动周期与锂增丰的关系. 本文利用自相关函数法提取出富锂巨星的自转周期并确定误差. 本研究发现, 对于A(Li)2 dex的巨星, 其自转周期分布较为弥散;A(Li)>2 dex的巨星, 其自转周期相对较快. 与此同时, 与之前研究相比, 富锂巨星的转动探测率(6.8%)显著高于巨星总样本(2.08%)[35].

2 样本选择及数据预处理

本文将Gao等[5]工作中用LAMOST搜寻的10525颗富锂巨星与Kepler任务的观测交叉, 获得619颗共同源, 其有效温度的范围为3900–5600 K, 表面重力加速度对数值lgg的范围是1.0–3.5 dex, 在Kiel图上的分布如图1所示.

图1 619颗富锂巨星在Kiel图(lg g-Teff)上的分布, 颜色棒代表锂丰度Fig.1 The Kiel diagram (lg g-Teff) of 619 Li-rich giants, the color bar represents the abundance of lithium.

由于本研究中所关注的由自转调制带来的恒星表面转动为低频信号, 往往大于1 d,只有采样间隔为29.4244 min的LC数据可以被用来研究. 在619颗富锂巨星中, 332颗观测源的光变曲线可以从MAST网站1https://archive.stsci.edu/index.html直接下载. 考虑到本文研究的巨星表面转动周期分布集中于10 d以上[35], 为了保证提取出的转动周期可靠, 本研究对数据质量有较高要求,因此选取了295颗观测数据大于30 d的源作为总样本, 与Yu等[36]对Kepler进行星震学分析的样本进行交叉, 获得星震学子样本共205颗以及剩余的90颗非星震学子样本. 在这里选择30 d观测时长作为良好数据的标准有两个: 首先是因为自转信号的探测需要观测时长覆盖多个周期才可被确认; 其次,Kepler卫星的观测是分季度(Quater)进行的, 对于仅有Q0一个月的数据或者只有其中某个季度不完整观测的观测源, 其数据质量不足以得到可信的分析结果.

NASA工作组提供了两种数据产品: 简单孔径测光(SAP)及预研究调节简单孔径测光(PDC)[37]. 前者作为原始数据包含多种仪器效应, 后者在一定程度上修正了仪器效应带来的周期信号影响, 但是对于提取出的周期信号, 尤其是长周期信号(100 d)依旧要小心应对. 本研究在提取表面转动周期时使用了PDC测光数据产品, 由于PDC的数据在之前的工作展现出的效果并不完美[38], 可能会存在被误认为自转调制的假周期信号, 本工作对提取出的周期信号进行了严格的筛选.

对于光变曲线的处理基本上遵循了Garc´ıa等[39]等在星震学分析预处理中的流程.由于同一颗恒星在不同季度(Quarter)可能由不同的电荷耦合元件(CCD)进行测光观测, 而CCD敏感度的区别会导致不同Quarter的数据有系统差, 这种系统差称之为跳跃值(jump). 为修正跳跃值, 通常会将后一段Quarter加减一个常数进行修正. 本研究中的常数是由前一段最后50个点中值与后一段前50个点的中值相减得到的. 通过对数据进行滑动平均, 当某一点的观测值偏离平均值5σ的时候认定为异常值(outlier), 将其剔除.同时, 由于数据采集中的间断会产生一个规律的窗函数, 对大振幅低频调制信号产生影响(如本工作中的自转调制现象). 为了减少这种影响, 对于光变曲线中的缺失值, 本文使用线性插值的方式进行补充. 大多数的工作会对光变曲线进行滤波[22,35,38], 本研究中,为了尽量保留所有的疑似转动信号, 没有进行滤波操作. 尽管这对之后信号证认造成了困难, 但是由于样本量较小, 可以逐个进行肉眼检查以确保结果准确性.

3 表面转动周期提取

本文使用的方法来自于McQuillan等[21]的工作, 其主要研究对象为矮星, 在其工作中同时使用了周期图的方法. 而本文研究的对象为巨星, 其星震学信号会十分接近自转信号, 因此傅里叶周期图的方法不够可靠. 于是本文仅使用了自相关函数法进行分析.在信号处理领域, 自相关函数可以写作如下形式

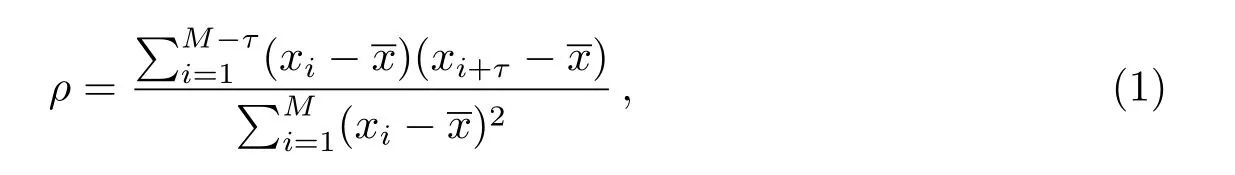
其中,ρ是对于一个时间序列xi(i=1,···,M)在延迟τ处的自相关系数, 其中M为时间序列的观测点个数.是时间序列的平均值. 如上文所述, 本文研究的是长周期转动信号,在这取τ <300, 代表小于300 d的自转周期可以提取.

转动周期的计算分为以下3步: 第1步依靠所计算的自相关函数值判断光变曲线是否具有周期信号, 第2步证认自相关函数图中的峰值, 第3步先是判断周期信号是否为转动信号, 如果是则选择与自转周期对应的峰值, 然后, 计算自转周期的误差. 其中, 第2步可以依靠多种峰值匹配算法进行, 本文使用的是Python中Peakutil软件包, 其原理为最小距离和最小峰值. 然而, 由于算法的不稳定性, 需要证认哪些峰是自转调制信号, 哪些峰是假信号, 这一步本文使用的是肉眼检查的方式来手动挑选.

在前两步中, 由于实际观测的光变曲线包含多种高频低频信号, 所以计算出的自相关函数值也不是十分的平滑, 会出现锯齿状结构, 所以首先需要对求得的自相关函数值进行平滑, 本研究中使用的是高斯窗, 窗的尺寸为240个观测点, 半高全宽为70个观测点.这个取值的依据在于平滑掉5 d以下的信号, 保留5 d及以上的信号. 在提供平滑的自相关信号的同时, 有利于提取自相关函数图中的峰值. 这时, 如果证认出的峰值小于3个,或者峰值的高度较小, 则认为这颗恒星不具有自转调制现象.

第3步中自转信号的证认依靠多种先验知识. McQuillan等[21]在2013年的研究中也进行详细介绍. 包含以下3种情况: 首先, 如果光变曲线包含的自转调制信号来自于一个演化缓慢的大黑子(群), 那么光变曲线会是一个良好的正弦/余弦状曲线, 反映在自相关函数上是多个等间隔、高度逐渐减小的峰. 那么第1个峰所在的位置即可被认为是自转周期, 其余谐频可以用来计算转动周期误差. KIC 2305930是本研究中的其中一颗恒星,它的自相关函数和光变曲线如图2所示; 其次, 光变曲线包含的自转信号来自于两个大黑子(群)的演化, 光变曲线会呈现两个下落趋势(Double Dip), 反映在自相关函数上是第2个峰会略高于第1个峰, 这时我们认为第1个峰为1/2自转周期, 第2个峰为转动周期,寻找第2个峰的谐频来进行误差计算, KIC 8479301是本研究中的其中一颗恒星, 它的自相关函数和光变曲线如图3所示; 最后, 由于仪器效应消除, 邻近源干扰等因素, 光变曲线可以很复杂, 尽管在自相关函数上依旧可以提取出周期信号, 但是在本研究中我们将其摒弃不用.

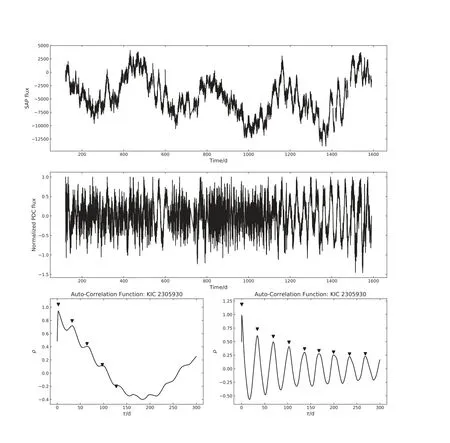
图2 KIC 2305930的光变曲线及自相关函数图. 上图为原始光变曲线; 中图是修正的归一化PDC光变曲线; 左下图为原始光变曲线得到的自相关函数, 右下图代表由修正的PDC光变曲线得到的自相关函数. 三角标志了自相关函数中的峰值,右下图中第1个峰值被认为是自转周期.Fig.2 The light curves and corresponding auto-correlation functions (ACFs) of KIC 2305930. The top panel plots the light curve of raw data. The middle panel represents the corrected normalized PDC light curve. The bottom two panels are ACFs of the two series of light curves, respectively. The triangles mark the peak location of auto-correlation functions. The first detected peak of bottom right panel is considered as rotation period.

图3 KIC 8479301的光变曲线及自相关函数图. 各子图与图2相同. 右下图中的第1个峰被认为是1/2自转周期.Fig.3 The light curves and corresponding auto-correlation functions of KIC 8479301. The panels are the same as Fig.2. The first detected peak of bottom right panel is considered as half rotation period.

将原始光变的自相关函数图与PDC光变曲线的自相关函数图相比较, 有助于对提取的周期进行进一步的确认. 若两者皆表现出类似的长周期变化趋势(>90 d), 则通过光变曲线进行进一步确认. 若前者提取出一个长周期变化而后者提取出一个短周期变化,则认为短周期信号为自转周期, 因为短周期信号在Kepler观测中更可靠, 而长周期信号更容易受到仪器效应的影响.

通过以上几步的筛选, 只有被认为是真正自转信号的自相关函数图才会进入第4步进行误差计算. 对于自转周期对应的横坐标τ, 计算相邻谐频的差值记为∆τ, 可以得到N–1个∆τ, 依靠以下公式计算误差

其中N为峰值的个数, MAD是每个∆τ与所有∆τ的中值之差的中值. 这种方式等效于求解高斯分布的标准偏差, 而这种方法对于偏离值更加稳健.

需要强调的是, 本文对于提取出的周期是否来自于恒星自转进行了比较严格的筛选, 最后保留的都是极大可能性的自转源, 因此所求的自转探测率实际为下限, 或许还会更高.

4 结果与讨论

如上文所提到的, 本文中的295个样本被分成了两部分, 其中205颗具有星震学演化阶段分类. Yu等[36]将样本中的巨星演化阶段分为3类: RGB、氦核燃烧星(HeB)以及未能通过星震学确认的恒星(Unknown), 这里我们使用了其结果. 剩余90颗没有星震学参数. 前者星震学样本共提取出14颗星的转动周期, 自转探测率为6.82%, 后者非星震学样本有22颗星提取出转动周期, 自转探测率为24.4%. 由于前者星震学样本的选择效应与Ceillier等[35]的样本基本一致, 两者都是Kepler搜寻到的震动恒星, Ceillier等[35]的样本仅在本工作星震学样本的基础上增添了少许样本. 其自转探测率仅为2.08%, 因此表现出恒星转动与巨星锂增丰现象的相关性. 尽管90颗非星震学样本的探测率无相同选择效应的样本进行比较, 但如此之高的巨星转动探测率也值得讨论. Drake等[30]在研究K型富锂巨星时也发现快速转动的巨星有很大部分为富锂巨星. 由于前者的星震学样本是选择了Kepler观测中具有长时间观测且有良好星震信号的样本, 而后者的非星震学样本观测时长较短或无星震学信号探测, 两者具有不同的选择效应. 这是由于在测光观测中, 星震学信号会对自转信号的探测产生副作用, 所以后者理论上也应当比前者有更高的探测率.

如图4展示了不同演化阶段富锂巨星锂丰度与转动周期的关系, 在探测到36颗有自转信号的恒星中, 只有2颗为RGB、11颗为HeB, 因此转动信号的测量展现出与演化阶段的相关性. 通过分析Ceillier等[35]的样本, 将其数据与Yu等[36]的数据进行交叉, 发现其工作从RGB与HeB个数大致相当的一万余总样本中, 提取出转动周期的恒星361个, 其中HeB的个数约为RGB的7倍, 与本研究中富锂巨星样本提取转动比例大致相似(11: 2),转动信号的测量同样展现出与演化阶段的相关性. 因此, HeB的确更容易被提取出转动周期, 可能的原因在于HeB相比RGB更强的黑子活动. 但从本工作的样本量(13颗)来看,尽管绝大部分为HeB, 但不能确定锂增丰现象与演化阶段是否具有相关性.

同时, 从图4中还展示出其他特点. 首先, 相比于锂增丰较弱的恒星其转动周期分布较为弥散, 对于锂增丰程度更强的恒星, 样本自转周期相对较短. 与早期的研究结果一致. 然而, HeB在富锂巨星样本中展现出较短的转动周期这一特性, 在普通巨星样本中不存在. 如图5来自于Ceillier等[35]的结果, 可以看到HeB和RGB的转动周期分布基本一致, 都是近似平均分布. 因此, 可以说出现锂增丰现象的HeB转动周期通常更短; 其次,在富锂巨星与极富锂巨星的分界处(约3.3 dex), 转动周期的演化被分为两个序列, 在极富锂巨星侧显示出更明显的转动越快锂增丰越强的特点. 两个序列的现象可能来自于数据量较小的巧合, 如果真实存在, 也可能暗示着对于富锂巨星和非富锂巨星存在不同的形成机制, 需要更多的观测数据去确认. 但两个序列都显示出与转动速度的相关性.

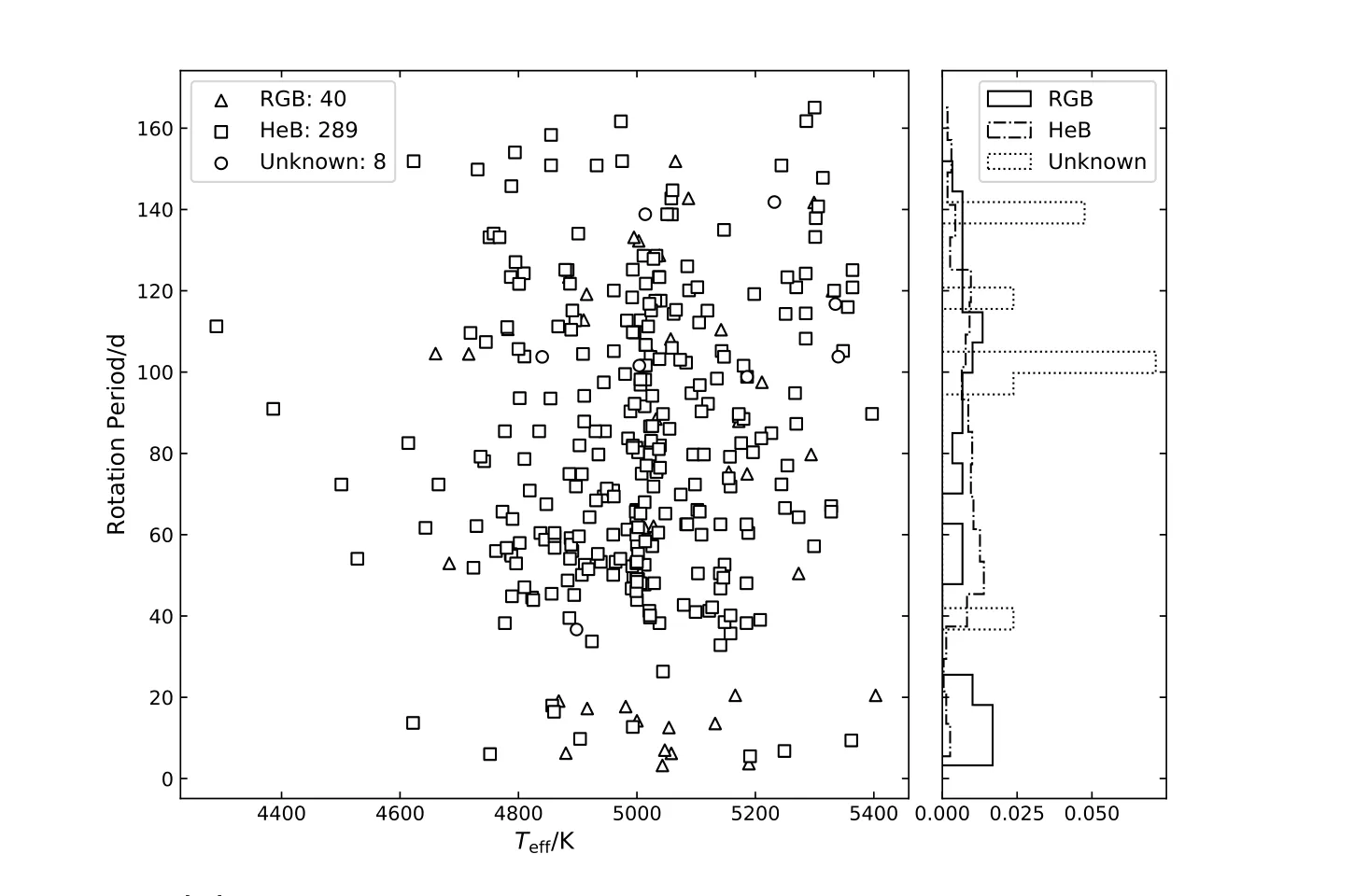
图5 左图为Ceillier等[35]2017工作中样本的恒星自转周期-有效温度分布图, 图例与4相同. 右图为转动周期对3类恒星的直方密度统计图.Fig.5 The left panel stands for the period vs. effective temperature of three classes stars, which have the same symbols as Fig.4. The right panel plots the histogram for rotation periods of three classes stars.

综上, 本文首次利用Kepler卫星提供的光变曲线研究了由LAMOST望远镜搜寻出的富锂巨星表面转动周期与锂增丰的关系并得到以下结果: (1)从转动周期的角度确认了转动与锂增丰具有相关性, 强锂增丰的星倾向于快速转动, 而相对弱锂增丰的星其转动周期分布相对弥散; (2)富锂巨星和极富锂巨星的转动速度随锂增丰强度或许存在两个演化序列, 在极富锂巨星侧显示出更明显的随转动加快锂增丰越强的特点, 由于样本量较少的原因, 还需要更多的观测确认, 如果此现象确实存在, 或许暗示两种不同的形成机制; (3)富锂巨星与演化阶段的相关性需要更大样本的数据去确认.

本研究中极富锂巨星锂增丰越强转动越快的观测结果, 可以将其归因于恒星Ω的增加可以增强Dmix并导致锂增丰(Dmix∝Ω2). 因此, 为由转动导致的额外混合机制提供了一定的支持. 但其中精确的物理图景仍不明确, 仍然需要更多的观测数据支持以及更精细的模型计算. 由于现有的模型并没有太多地考虑表面转动的效应, 未来的工作可以在讨论形成机制的时候计算自转和锂丰度的分布, 并与本观测进行比较.