潮汐能量耗散与地月系统演化∗

高布锡

(中国科学院精密测量科学与技术创新研究院武汉430077)

1 绪论

地月之间距离的长期变化, 主要是由于月球引起的潮汐耗散引起的. 月球对海洋上潮汐隆起的微小引力是原始的引潮力, 它正比于潮汐的高度, 而海潮高度反比于地月之间距离的立方[1]. 因此利用开普勒第3定律, 可以导出月球的引潮力位正比于月球平均运动的平方. 根据月球的平均运动以及它的加速度, 月潮的能量耗散可以被计算出来. 如果采用现代的月球平均运动加速度值−25.90′′·cy−2, 地月距离的演化就能被反推出来[2].但是计算结果显示, 在28亿年前地月距离迅速减小, 甚至趋向于零. 某些学者推算地月系的演化过程也得到了同样的结果[3–7]. 这个事件被称为格斯科恩事件, 显然这是不可能的. 因此采用现在的月球平均运动加速度值来反推地月系统的演化, 显然是不合适的.现在月球平均运动加速度值为−25.90′′·cy−2, 它大于用古生物钟给出的结果. 如果采用月球平均运动加速度值为−20.72′′·cy−2, 它等于现在月球平均运动加速度值的0.8倍, 则推算结果表明, 在35亿年前地月距离是0.18百万公里. 因此直到35亿年前格斯科恩事件都可以避免.

地球自转速率变化的长期项主要受3个因素影响. 最主要的贡献是月球潮, 第2个因素是太阳潮. 由于地球位相的变化, 月球潮和太阳潮总是互相加强或者抵消, Gao[8–9]曾估计太阳潮贡献的能量耗散仅仅是月球潮的1/6. 第3个因素是地球极角动量矩的变化.太阳潮和地球极角动量矩变化对月球自转长期变化的贡献可以认为是固定的. 因此可以推导出过去35亿年以来的回归年日数变化. 例如在33亿年前, 日长约为9.6 h, 一个回归年中有913.2 d.

在大碰撞之后[10], 吸积过程曾使得月球达到融化的温度[11]. 但是根据热模型显示,月壳在50–100百万年间迅速冷却[12]. 随后从40到38亿年前发生了后期大轰炸事件[13].月球自转形成与轨道同步应该是在后期大轰炸事件之前. 由于早期月球离地球很近以及地球的强大引力场, 绝大多数陨石落在了月球的背面, 它们形成了厚厚的覆盖层, 并且导致了月球的形状中心对月球质心有1117 m的偏离(根据嫦娥月球模型CE-1). 虽然现在的月球没有磁场, 但是月球岩石显示在39–36亿年前曾有剩余磁场[14]. 所以可以估计除月核外月球的凝固时间大约在35亿年前.

假定月球在自转离心力和地球的引潮力作用下形成三轴椭球体, 月球表面形成等位面. 再假定月球冷却后一直保持它的化石形状至今, 那么根据月球的三轴椭球体形状可以算出在35亿年前, 地月距离应该等于1.7455×108m, 月球的自转周期等于3.652 d[15–16]. 根据开普勒第3定律, 恒星月的长度应该等于8.34 d. 但是后期大轰炸可能部分地破坏了月球的平衡面形状, 因此上述关于地月距离以及月球自转周期的数值可能并不精确.

2 地月距离的演化

月球引起的潮汐摩擦耗散使得地月距离逐渐变大, 并使得地球自转逐渐变慢. 海洋上的潮汐隆起总是略微超前于月球轨道, 并且产生一个小的引力拖住月球, 这个力等于总的潮汐摩擦力. 潮汐与地球表面的摩擦力使得地球自转变慢. 月球对潮汐隆起的引力正比于潮汐隆起的质量, 而潮汐隆起的质量正比于潮汐的高度. 所以可以简单地假定潮汐摩擦力正比于潮汐的高度(见图1). 潮汐的高度反比于r3, 在这r是地月之间的距离[1]. 应用开普勒第3定律n2r3=f(M+m), 可以导出月潮引起的潮汐摩擦耗散正比于月球的平均运动n的平方, 其中,f是万有引力常数,M、m分别是地球质量. 因此t为时间. 在这C和ω分别是地球的极惯量矩和自转角速度. 根据地月系统的角动量守恒定律, 可以给出[8–9]：

i是月球轨道的倾角,K是常数. 不考虑太阳潮的影响, 假设地球的极惯量矩C是常数, 利用(1)式, 月球平均运动n的演化可以用(2)式计算：

A是一个常数, 它可以从求得.n0是现在的月球平均运动,0是现在月球平均运动的长期加速度. 将(2)式积分, 可以得到：

其中,t0为起始时间.

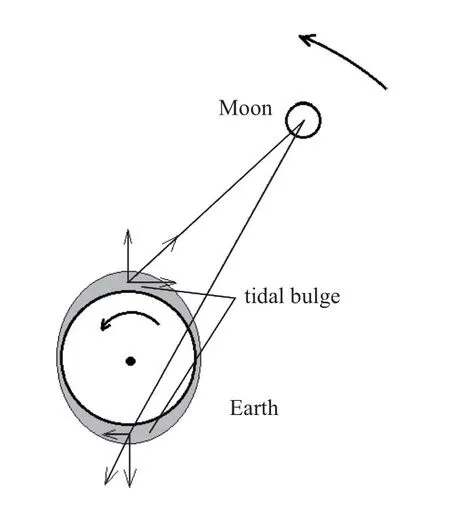
图1 月潮引起的能量耗散正比于海洋潮汐的高度Fig.1 Energy dissipated by lunar tide is proportional to oceanic tidal height

为了计算现在的月球平均运动长期加速度值0, 1995年Yoder[2]根据多种不同测量方法得到了数值相互符合的结果. 不妨取

由此可算出现在地月平均距离每年增加3.83 cm. 现在月球n0= 13.17636◦·d−1, 根据n0和0的数值, 利用(3)式可以得到计算n的公式：

利用开普勒第3定律, 可用下式计算地月距离,

现在的月球平均运动加速度绝对值是比较大的, 它比自奥陶纪(the Ordovician age)以来用古生物钟获得的平均数值大1.4倍[17]. 1982年Webb[7]采用半球海洋模型发现,假如地球自转速率比现在的数值增大1倍, 那么在海洋中的潮汐能量耗散将减少约1/3.大陆漂移大约发生在两亿年前, 它改变了海洋的形状, 分裂的大陆可能更强烈地阻止潮汐的流动, 增加了潮汐能量耗散. 因此现在的潮汐能量耗散可能是有史以来最大的. 但两亿年相对于35亿年的地球演化历史是个很短的时间, 因此在以下的计算中将忽略由于大陆漂移造成的影响.

利用(6)式并采用绝对值较小的月球加速度值−20.72′′·cy−2, 就可以算出35亿年以来地月距离的演化. 在图2中用实线表示了这个变化.

图2 过去35亿年来地月距离的变化Fig.2 The change of distance between Earth-Moon during past 3.5 billion years

3 地球自转速率的演化

有3种因素影响地球自转速率的长期变化, 它们是月球和太阳引起的潮汐耗散以及地球的极惯量矩的变化. 设是地球自转角速度的变化率, 有

其中,mt为月潮引起的地球自转速率变化,st为太阳潮引起的地球自转速率变化,nt为非潮汐因素引起的地球自转速率变化.

潮汐能量耗散主要是由于月潮引起的. 暂不考虑日潮的影响以及地球极惯量矩的变化, 利用(1)式, 可给出月潮引起的地球的自转速率变化公式,

将(8)式积分, 就可以导出计算ωmt的公式,

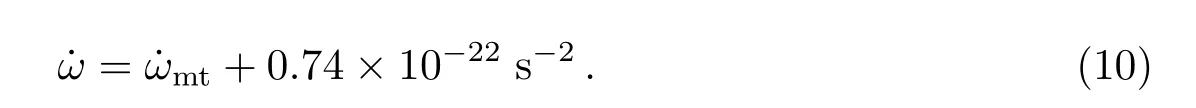
利用(5)、(9)和(10)式, 可以求得上溯到35亿年前ω的数值. 考虑到日月潮汐摩擦以及地球惯量矩的变化, 可以算出, 现在=−5.405×10−22s−2, 相对于日长的长期变化为2.01 ms/cy.

用N表示回归年日数, 可以用下式求得[8–9],

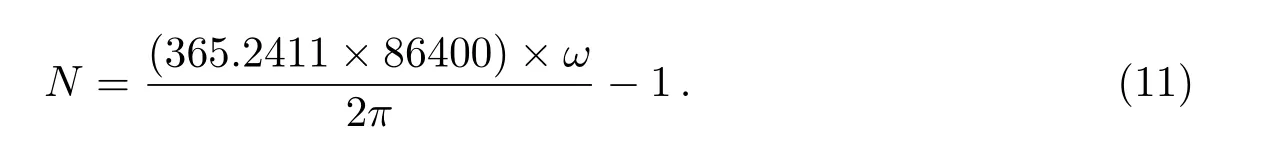
在图3中描述了35亿年来回归年日数N的变化, 可以看出在34亿年前回归年日数等于1000 d左右.

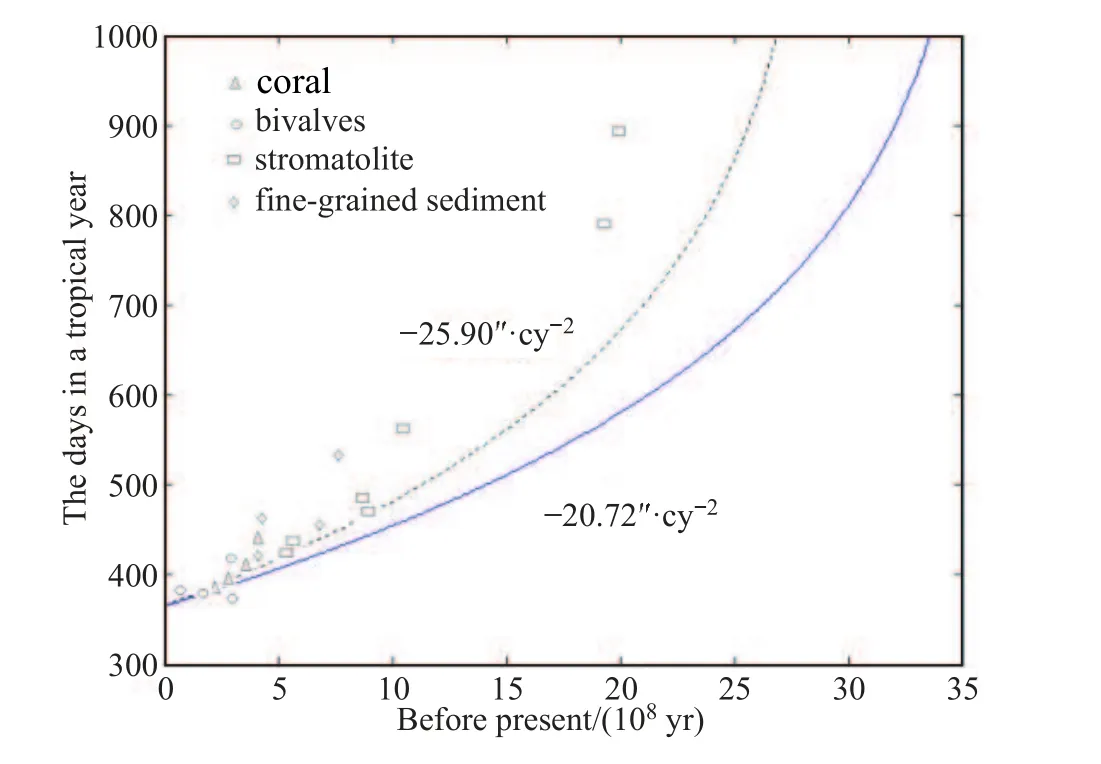
图3 过去35亿年来回归年日数的变化Fig.3 The days in a tropical year during past 3.5 billion years

4 古生物钟数据与理论数据的比较

最重要的古生物钟是珊瑚、贝类以及蓝藻形成的叠层石化石. 某些软体动物的壳保存了一些连续的层, 它们反映了天文现象的周期变化. 周日结构的生长与太阳的照射以及潮汐高度的变化有关. 古生物钟化石累积的沉积层密度的变化反映了季节变化, 从而给出了回归年日数的数据. 沉积层密度的变化也反映了潮汐的逐日变化, 从而给出了朔望月日数的数据. 因此测量古生物钟的层状结构可以知道古地质时期时的回归年日数和朔望月日数.

在图3中, 用不同符号标识了采用不同的古生物钟化石求得的回归年日数变化. 但是珊瑚和软体动物的结果只能给到5亿年前. 叠层石是最古老的古生物钟, 至今为止,只有叠层石的资料可以提供在寒武纪时反映地球自转历史的资料. Pannella[19]曾研究最古老的叠层石(28亿年前)显示了由于潮汐变化而产生的周期为10、20和40 d的变化.从Biwabik得到的叠层石化石显示在20亿年前一年有800–900 d[20]. 然而更古老的叠层石的数据并没有能够提供季节变化的数据. 其原因是这些叠层石化石的层状图像, 特别是季节的图像十分不清楚.

在太古纪(28亿年前)早期太阳的光度是微弱的[21], 但是早期的地球大气富含CO2、CH4和N2. 由于温室效应地球气候是温暖的[22], 使得蓝藻大量增加, 蓝藻的光合作用使得大气中的二氧化碳含量急剧减少, 氧气成分增加. 由于蓝藻的沉积和粘合形成了叠层石. 太古纪的锆石表明在44亿年前地球表面有水[13], 为了解释叠层石的形成同样也需要假设在38亿年前地球表面有液态水的海洋. 叠层石的沉积层提供了朔望月日数, 但是由于有周日潮和半日潮, 在1 d中可形成双沉积线. 因此预先知道合理的天文韵律, 对于做出正确判断是很重要的[11]. 另外一种地球古自转的证据是细砂粒沉积形成的韵律.在7.5–6.5亿年前, 在澳大利亚Neoproterozoic沙砾的沉淀层, 被解释为是记录了古潮汐周期的韵律[23–24], 其结果显示在6.5亿年前每年有13个月和450 d.

假定回归年的长度是固定的, 那么根据地月距离数值, 就可以推算出恒星月的长度.在本文中已经求出了回归年日数, 因此朔望月的日数(N2)也能够计算出来, 计算结果见图4. 可以看出直到28亿年前在N2的变化是很小的, 其最大值是在约18亿年前, 一个朔望月约有32.4 d. 根据古生物钟资料得到的朔望月日数与图4中的曲线符合很好[19,25].在28亿年前N2的数值很快减少到20 d. Pannella[19]、Cao[26]和Zhu等[27]曾经在古老的叠层石化石中发现了40–45 d的潮汐生长线, 作者认为它们很可能是朔望月周期的加倍.

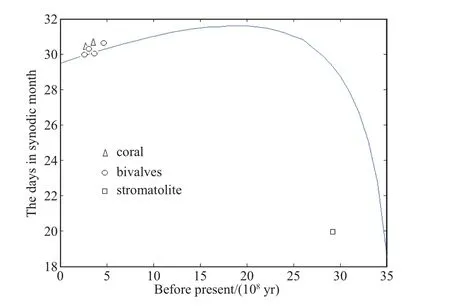
图4 过去35亿年来朔望月日数的变化Fig.4 The days in a synodic month during past 3.5 billion years

利用不同的古生物钟和沙粒沉淀形成的韵律所求得的回归年日数被采用不同的符号标志在图3上. 可以看出直到8亿年前, 古生物钟的结果与理论结果都是符合得很好的.但是8亿年前叠层石的数据大于理论值. 在20亿年前回归年日数等于800–900 d太大了,是不可能的. 1972年Pannella[19]曾经指出在叠层石的9–10个沉淀线之后紧随着4–5个沉淀线是经常发生的. 由于1 d内有两个潮峰, 并且在太古纪叠层石化石的季节韵律是十分不清楚的, 所以这些叠层石给出的回归年日数的变化结果是值得商榷的, 但是给出的朔望月日数的变化, 即潮汐周期的变化是很有意义的, 它较好地反映了地球的古自转历史.

5 总结

30亿年以来潮汐能量耗散成为影响地月系统演化的重要因素. 地月距离变得越来越远, 地球的自转速率也变得越来越慢. 在本文中给出了地月距离和回归年日数的演化曲线. 理论数据与古生物钟的结果直到8亿年前都基本上符合.

忽略太阳潮引起的能量耗散, 地月系统的角动量守恒是正确的. 但是地月系统的能量守恒是不正确的. 由于月球潮汐引起的摩擦使得地球自转角速度变慢, 现在数值为=−6.145×10−22s−2. 因此地球自转的能量耗散率为−3.6×1019erg/s. 同样根据月球平均运动的加速度0=−25.90′′·cy−2可以算出月球轨道运动的能量增加值为1.22×1018erg/s. 因此只有约3%的地球自转能转化为月球的轨道运动能. 绝大部分能量(约97%)耗散在地球表面上.

地月系统的演化过程是十分复杂的. 大气、海洋以及大陆的变化都能够影响地球自转速率的演化, 例如, 在1991年Young[28]曾经指出至少在大陆上有11个主要的冰期被确认, 冰期存在的时间大约占地球历史的5%–10%. 在冰期时许多海洋都冻结了, 所以潮汐能量耗散将变得较小, 因此地月系统的动力学演化过程将变慢. 在本文中, 只是给出了地月系统的大致演化过程. 还有许多其他的自然因素也会影响地月系统的动力学演化,它们都需要更多的古地质资料才能估计.致谢 感谢钟敏教授和张子占博士的帮助.