热海王星系统HD 106315的近2:1平运动共振捕获与轨道演化∗

黄秀敏 季江徽 董 瑶

(1 中国科学院紫金山天文台南京210023)(2 中国科学院行星科学重点实验室南京210023)(3 中国科学技术大学天文与空间科学学院合肥230026)

1 引言

1995年, Mayor和Queloz[1]利用视向速度测量法在类太阳型恒星51 Pegasi周围发现第1颗热木星, 他们也因此分享了2019年诺贝尔物理学奖. 随着测量精度的不断提高, 截至2019年12月天文学家通过视向速度法(Radial Velocity)、凌星法(Transit)、微引力透镜法(Microlensing)、直接成像法(Direct Imaging)、天体测量法(Astrometry)等手段[2],发现并确认4100多颗系外行星(exoplanet.eu). 这些行星大小不一形态各异, 包括热木星(Hot Jupiters)、亚海王星、类地行星、超级地球(super-Earth)等类型, 它们怎样形成以及轨道构型如何演化, 无疑是当前系外行星研究的前沿科学问题.

在发现的系外行星中, 有一类天体的质量接近海王星且其离恒星的平均距离约为1 au (天文单位)以内, 通常我们称之为热海王星(Hot Neptunes). 目前观测统计表明, 在已发现的300余颗热海王星中偏心率较大(>0.2)的约占1/4, 分别分布于27个不同的行星系统[3].

作为Kepler空间探测任务的延续, K2在2014年至2018年3月完成了16期观测工作并发现数百颗系外行星[4–5]. 而本文的研究对象热海王星系统HD 106315正由K2任务所发现. 恒星HD 106315距离地球(107.3±3.9)pc, 它是一颗质量和半径与太阳相似的F光谱型恒星, 年龄约为40亿年, 其质量为(1.07±0.03)M⊙, 半径为(1.18±0.11)R⊙, 有效温度为(6290±60)K[6]. 该行星系统中包含两颗大偏心率的热海王星, 表1中列出了HD 106315系统两颗行星的轨道观测数据, 其中,M为行星质量,M⊕代表地球质量,Rp为行星半径,R⊕代表地球半径,R⋆为中央恒星半径,P为行星轨道周期,i和ω分别为轨道倾角和近星点幅角. HD 106315b和HD 106315c在密近轨道上(轨道半长径a分别为0.09012 au和0.1526 au)以较大的轨道偏心率e(分别为0.3和0.23)围绕明亮的中央恒星运动. 这两颗行星轨道周期比接近2, 故它们围绕中央恒星的轨道呈近2 : 1平运动共振构型. Yimathlmaz等[7]还指出行星HD 106315b的主要组成为50%的水和50%的岩石, 介于气态行星和岩石行星之间. 结合视向速度测量结果, 这两颗行星的质量、内部结构及大气特征值得关注. 其他研究表明, 该行星系统在更长周期的轨道上还可能存在第3颗行星[6].

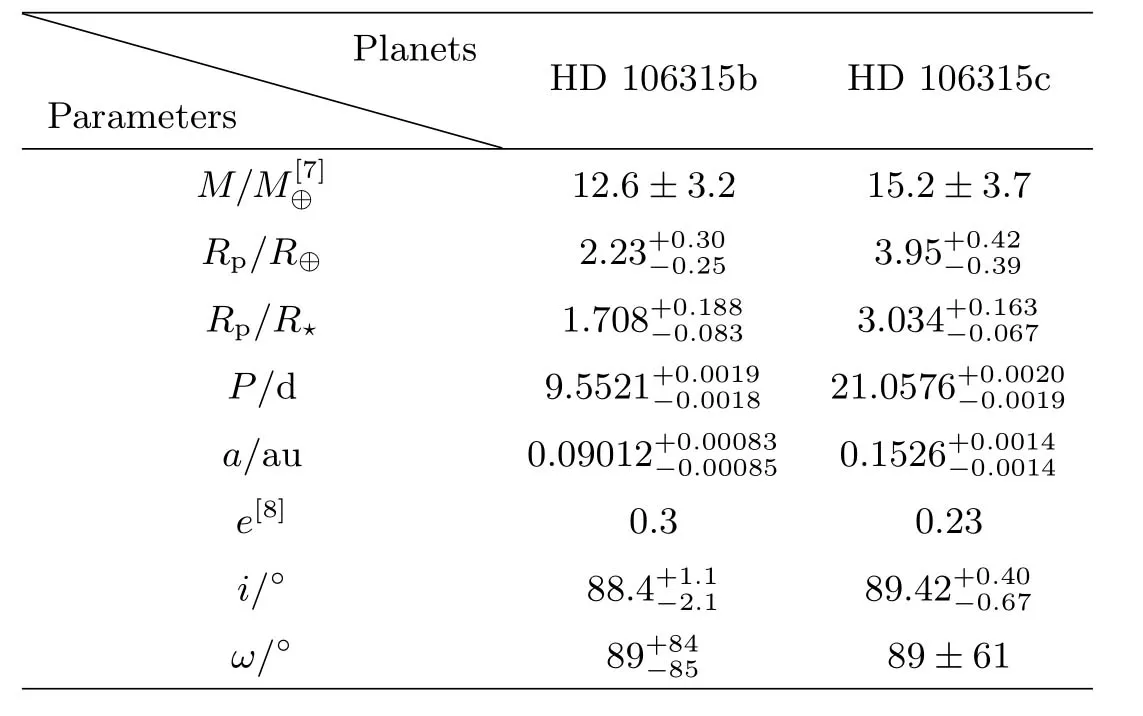
表1 HD 106315系统行星参数[6]Table 1 Planetary parameters of HD 106315 system[6]

通过对Kepler多年观测的数据分析[9], 科学家发现有很多系外行星系统呈现平运动共振(Mean Motion Resonances, MMRs)轨道构型. 法国数学家和物理学家Laplace最早将轨道共振比率定义为两颗行星围绕同一中央恒星在相同的时间间隔内完成轨道数的比例, 即两星轨道平运动速率n′和n呈整数比:n′/n=p/(p+q)(p、q均为正整数). 此时,行星轨道周期也呈现对应的整数比(p+q)/p. 系外行星中常见的共振轨道构型有2 : 1、3 : 2共振[10], 其中2 : 1平运动共振十分普遍[11–13], 凌星法发现的行星系统中有16%显示为近似2 : 1平运动共振行星系统, 2 : 1共振也被认为是行星系统演化过程中比较稳定的轨道构型. 此外还有一类特殊的平运动共振—3体共振(也称为Laplace共振)[14–15], 是指系统内3颗行星两两处于2 : 1平运动共振, 例如太阳系内木星的3颗卫星Ganymede、Europa、Io就是4:2:1轨道构型.

在系外行星系统中与HD 106315行星系统类似的近2:1平运动共振有很多, 例如GJ 876、GJ 1061、HD 136352等. GJ 876[16]系统中的GJ 876b和GJ 876c质量接近木星质量, 而HD 106315b和HD 106315c为海王星质量行星. 在考虑行星与原行星盘相互作用时, GJ 876行星系统由于质量更大而可能形成原行星盘内间隙环(gap), 从而使行星之间的盘内物质被快速清除, 抑制了外部轨道行星进一步向内迁移. 对于HD 106315行星系统, 需要判断行星质量是否满足产生间隙环的条件, 进而影响后续的轨道迁移过程. 同时, HD 106315行星系统构型更紧凑, 恒星引力和行星间的摄动作用对行星共振迁移的影响也会更显著.

对于轨道半长径小于0.1 au的热海王星, 来自中央恒星的潮汐耗散效应也会对轨道半长径和偏心率产生影响. 与轨道迁移相比, 潮汐耗散作用时标更长, 对于海王星质量的行星, 该潮汐耗散时标通常大于106yr. 通过对HD 106315轨道演化机制的研究, 我们可深入了解大偏心率热海王星系统演化历史及当前系统稳定性.

综上所述, 本文工作将围绕热海王星系统HD 106315近平运动共振构型的形成机制和轨道迁移模型展开. 第2节简要介绍HD 106315系统的轨道演化动力学模型, 包括I类轨道迁移和共振捕获. 第3节给出本文使用的参数空间和数值模拟方法, 并据此得到观测值对应的近2:1共振轨道构型及初始轨道参数范围. 第4节考虑了潮汐耗散效应, 结合半分析方法和数值模拟, 讨论HD 106315系统在不同轨道构型下的潮汐演化结果. 第5节总结了HD 106315系统轨道迁移机制和潮汐效应对轨道共振构型的影响.

2 轨道迁移模型

2.1 HD 106315系统的I类轨道迁移

一般认为, 行星起源于围绕在年轻恒星周围的气体和尘埃盘. 在恒星引力主导的收缩过程中, 气体和尘埃因具有不同的角动量, 被分配到空间不同位置. 角动量小的物质被吸引到系统中心, 角动量大的物质形成原行星盘. 根据Hayashi[17]等提出的原行星盘经典物理模型, 原行星盘直径范围为10–1000 au, 寿命约106–107yr.

根据系外行星原位起源(in-situ)模型和Lee等[18]的工作, 在距离中央恒星大约0.1 au处质量为10M⊕的原行星可以达到雪崩吸积(Runaway accretion)的临界核质量, 在百万年内快速吸积气体生长为气态巨行星. Hansen等[19]和Chiang等[20]提出了类海王星行星的原位吸积模型, 行星在当前轨道附近直接通过尘埃吸积和行星子(planetesimals)并合形成. 他们认为, 目前观测到的超级地球和类海王星行星形成于气体耗散殆尽的过渡原行星盘中, 一般不会经历剧烈的角动量交换过程, 从而易保持行星形成时刻的近圆轨道.

HD 106315系统内两颗行星均处于短周期密近轨道, 但是轨道偏心率较大. 这意味着该行星系统更可能通过轨道迁移机制形成, 且轨道迁移过程中可能存在不稳定的轨道偏心率激发和衰减. Terquem等[21]通过对质量为0.1∼1M⊕的原行星轨道演化进行数值模拟, 发现它们可以并合形成海王星质量的行星, 且这些类海王星行星相伴出现, 形成多行星系统. Cresswell等[22]指出, 对于无法形成原行星盘环形空隙的类海王星行星, 其轨道偏心率和轨道倾角受盘内气体耗散作用的衰减时标远小于轨道迁移时标.

原行星盘驱动的轨道迁移模型中, 行星和气体盘之间产生不可逆的角动量交换,轨道迁移的速率是由气体盘的物理参数和行星质量决定的. 根据行星的质量不同, 一般分为两种类型的轨道迁移机制: 第I类迁移(type I migration)和第II类迁移(type II migration). 类地行星和类海王星往往启动速度较快的第I类迁移, 质量较大的气态巨行星则会发生第II类轨道迁移, 且在其轨道附近形成空隙环, 使行星周围尘埃和气体密度下降, 共旋力矩(corotation torques)和Lindblad力矩[23]影响减小, 进而减慢行星迁移速率.

对于HD 106315系统, 考虑I类轨道迁移. I类轨道迁移速度较快, 地球质量的原行星可在105yr内到达中央恒星处. I类轨道迁移时标具体还取决于行星盘的结构、行星质量比、行星盘表面密度等. 同时, 两颗行星轨道倾角差值较小, 根据行星盘内的轨道迁移平面效应理论, 可以假设轨道迁移初始时刻两颗行星共面.

针对HD 106315行星系统从行星诞生后不久开始的轨道迁移过程, 我们首先考虑原行星盘内残余的气体和尘埃对行星轨道迁移动力学模型的影响. 原行星盘通过这些作用力对行星施加外部力矩, 为了保证这类力矩的持续性, 需要行星在原行星盘内稳定地迁移并且没有较大质量的吸积. 根据Masset等[24]早期工作中提出的观点, 行星受到的共旋力矩与其轨道迁移速率成比例, 且会对轨道迁移产生正反馈, 加快迁移速率.

在行星迁移的初始时刻, 通常假设两颗行星位于相距较远的两个轨道上, 以使行星轨道迁移的时标尽量小于行星盘星云物质完全耗散所需的时间. 一般可以假设行星b和行星c的初始轨道半长径a之比为ab:ac≈1:2. 行星迁移的时标是行星盘粘度系数的函数, 即原行星盘内轨道迁移的速率·a是行星盘粘滞系数v的函数[25]:

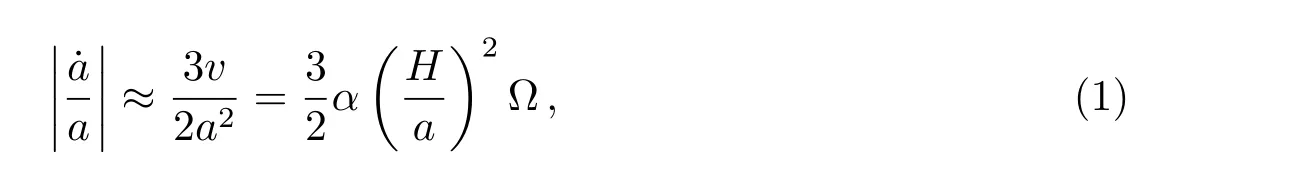
式中原行星盘粘滞系数[26]v=αH2Ω,α是用于表征原行星盘粘性程度的无量纲参数,H为原行星盘标高, 此处Ω是在行星轨道半长径为a时的Kepler公转角速度. 原行星盘内可能的粘性来源主要有: 磁转动不稳定性(Magnetorotational Instability, MRI)激发的磁流体动力学扰动以及由地球质量的行星激发的密度衰减[16]等.

2.2 HD 106315系统的共振捕获

在行星系统演化后期通常会形成稳定的平运动共振轨道构型, 目前系外行星共振捕获理论包括: 原行星盘驱动迁移模型、行星子散射迁移模型和潮汐演化模型[27]. 在不受外部扰动作用下, 行星不再产生剧烈的轨道迁移. 由于此时行星盘内剩余的气体对行星产生作用很小可以忽略, 若行星质量足够大且轨道偏心率较小, 那么两颗行星的轨道相对位置会长期保持稳定而形成所谓的“共振锁定”现象. 描述共振轨道构型的共振角为:θ=(p+q)λ′−pλ −qϖ′.λ′和λ分别为两颗行星的平运动经度:λ=n(t −tσ)+ϖ,其中,ϖ和ϖ′分别为两颗行星的近星点经度,ϖ ≡Ω+ω, Ω为轨道升交点经度,ω为近星点幅角. HD 106315系统当前轨道构型处于近似2 : 1平运动共振, 下文将主要围绕HD 106315系统进入2:1共振捕获的机制进行讨论.

在行星形成初期,轨道偏心率一般都较小. Batygin[27]提出,对于同样的初始偏心率,随着行星质量比m1/m2以及行星总质量与中央恒星质量比(m1+m2)/m0同时增大(下标0、1、2分别表示恒星和内、外行星, 下文同), 确定形成共振捕获的概率也越大. 他们还发现当m1/m2= 1, (m1+m2)/m0= 10−5,e1和e2均小于0.03时对应2 : 1平运动共振捕获概率为100%. 对于HD 106315行星系统,m1/m2=mb/mc= 0.829, 接近1, 且(mb+mc)/m0=7.87×10−5, 随着两颗行星偏心率增大, 2:1共振捕获概率逐渐减小, 对应的2:1共振捕获临界偏心率为emax=0.08.

同时, Batygin[27]还在研究木星和土星共振构型时得出2 : 1共振捕获概率随行星近星点经度差值∆ϖ的等高线图, 当∆ϖ=π时, 行星确定形成共振捕获的数据覆盖范围最小, 当∆ϖ= 0时, 行星确定形成共振捕获覆盖的参数范围最大. 因此, 我们在设置HD 106315行星系统的轨道初始参数时, 两颗行星的初始轨道近星点经度均设为0.

当行星轨道形成稳定共振构型之后, 其偏心率演化是由近星点平均进动速率决定的. 两颗行星近星点轨道进动速率达到同步时, 轨道偏心率也会受到激发. 且在实际迁移过程中, 存在一个偏心率衰减模型, 该衰减项与行星间的平运动共振作用对偏心率的激发项达到平衡, 此时偏心率会停止增长. 因此通过调整偏心率衰减的数学模型可以改变共振捕获后的偏心率平衡值, 以此得到接近观测值的轨道迁移机制. 该结论将应用到数值模拟的参数空间选择中.

3 数值模拟与结果分析

3.1 MERCURY6算法

传统的N-Body动力学积分算法在进行长时间的积分时无法避免产生累积的能量误差, 且积分速度较慢. 本工作在对HD 106315行星系统进行数值模拟时将采用辛算法积分器[28], 它不会产生长时间的能量误差累积, 并且当系统内行星数量较少、天体质量较集中时, 积分的速度将更快. 但是, 辛算法的缺点是当两颗行星发生近距离交会时, 积分结果会变得不精确. 为了解决这个问题, 我们采用了适用于N-Body问题积分的MERCURY6算法包[29], 在处理天体近距离交会问题时使用传统的积分方法, 其余部分采用混合辛算法(Hybrid Symplectic).

在对HD 106315行星系统进行轨道迁移数值模拟时, 除了考虑中央恒星的引力作用和行星之间的摄动作用, 还将考虑加入原行星盘耗散效应后的行星轨道迁移动力学模型. 由于原行星盘的耗散作用会使轨道半长径和偏心率产生衰减, 我们在HD 106315系统迁移模型中添加了准确的半长径a和偏心率e指数衰减项, 所以可以将哈密顿函数对应分解为3部分:Ha、He和Hgrav(即分别由轨道半长径a和偏心率e的衰减以及引力作用项表示的系统能量函数), 并将半长径和偏心率的衰减项写成哈密顿函数具体积分项的形式. 行星b轨道迁移的启动时刻受到行星c迁移速率的影响, 我们固定行星c初始时刻的轨道迁移速率为·ac, 假设原行星盘中的行星偏心率衰减速率满足Lee等[16]提出的由原行星盘耗散效应产生的轨道迁移偏心率衰减模型, 我们仅考虑行星c的偏心率衰减,即e的衰减速率满足: ·e2/e2=−K|·a2/a2|. 其中衰减系数K是无量纲的正常数. 鉴于·a/a和·e/e实际上是半长径和偏心率变化的时标(倒数),K值实际上是偏心率变化时标和半长径变化时标之间的比值, 偏心率最终平衡值只与K相关.

3.2 参数空间与轨道迁移结果

常见的设定轨道初值的方法有: 固定两颗行星的初始位置, 改变行星迁移的速率;或固定行星迁移的速率, 改变两颗行星的初始轨道位置. 这两种选取参数空间的方法均可以使行星在一定时间内迁移至目标轨道位置, 且可通过空间尺度与时间之比进行等价变换. 根据2.1节介绍的第I类轨道迁移半长径和偏心率演化模型, 可初步判断行星轨道迁移初始阶段在原行星盘内的相对位置, 但由于初始时刻行星的具体轨道位置与迁移时标均未知, 本文在一定初始轨道范围内固定两颗行星半长径比值及行星c初始时刻迁移的速率, 同时设定轨道迁移时标为105yr. 假设初始轨道半长径满足ac,0/ab,0= 2或接近此值, 以避免两颗行星因初始时刻相距过近而过早地产生密近交会, 从而使积分过快停止. 假设HD 106315c的轨道迁移速率满足: ·ac=−5×10−5au·yr−1, 再根据2.2节, 当两颗行星偏心率均小于0.03时, 将100%形成2 : 1平运动共振捕获, 随着偏心率增大, 形成2:1共振捕获的概率将减小.

现设两颗行星轨道初始偏心率均为e= 0.01, 其余轨道参数设置如表2所示. 表中所列的几组轨道半长径是经过模型线性化假设得到的初始参数组合,Pc/Pb是数值模拟得到的两行星轨道周期比. 其中, 初始值ab,0= 0.2–0.6 au、ac,0= 0.4–1.2 au得到的轨道周期比为2 : 1. 图1中所示为ab,0= 0.2–1.0 au、ac,0= 0.4–2.0 au时分别对应的轨道周期比变化图像. 在初始偏心率等于0.01的情形下,ab,00.6 au、ac,01.2 au时, 可形成2:1平运动共振捕获. 当ab,0=0.8 au、ac,0=1.6 au和ab,0=1.0 au、ac,0=2.0 au时,HD 106315系统会分别进入3 : 2和4 : 3平运动共振捕获. 所以根据共振比确定轨道迁移的初始半长径范围为: 0.2 auab,00.6 au、0.4 auac,01.2 au.

表2 初始轨道参数及对应轨道周期比Table 2 Initial orbital parameters and corresponding orbital period ratio

图1中, case1和case2在形成2 : 1共振捕获一段时间后, 对应的轨道周期比均出现下降, 这是由于两颗行星初始时刻轨道位置比较靠近, 第I类轨道迁移速率较快, 两颗行星周期比迅速减小从而脱离2:1平运动共振.

除了满足2 : 1平运动共振捕获, 还需要两颗行星轨道半长径能迁移到观测值附近,即接近ab= 0.09012 au、ac= 0.1526 au. 使用表2中的参数进行数值模拟, 得到图2所示的轨道半长径演化图像. 在case1–case4中, case1和case3会因发生近距离交会而使系统失稳, 只有在case2中, 当ab,0∼0.4 au、ac,0∼0.8 au时, 两颗行星半长径可以同时稳定迁移到当前观测数值附近(行星b和c当前轨道半长径分别为0.09012 au和0.1526 au),且在65000 yr附近两颗行星轨道半长径之差约为0.06 au. 故ab,0∼0.4 au、ac,0∼0.8 au可能是符合HD 106315行星系统轨道迁移的初始轨道位置.

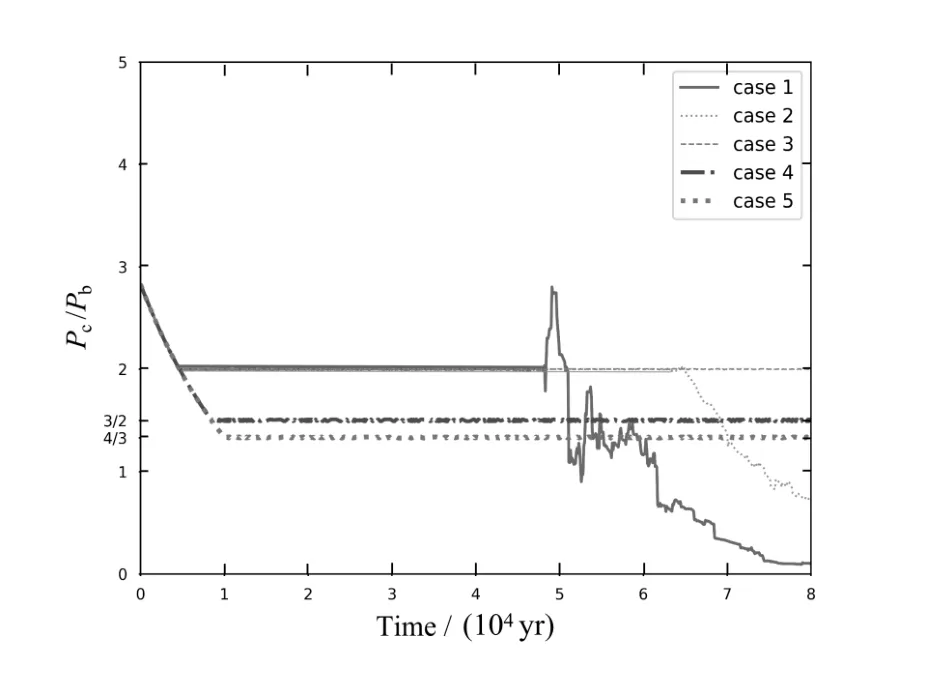
图1 不同初始轨道半长径下得到的轨道周期比Fig.1 Orbital period ratio of planets with different initial semi-major axes

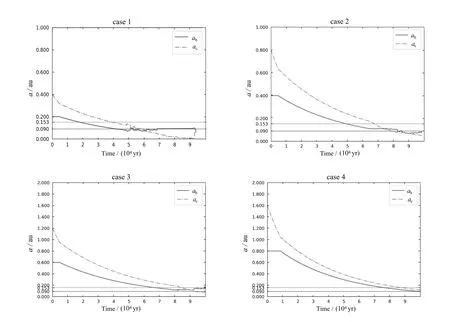
图2 不同初始轨道半长径下的行星轨道半长径演化Fig.2 Evolution process of planetary semi-major axis with different initial semi-major axes

在HD 106315初始半长径分别为ab,0= 0.4 au、ac,0= 0.8 au、eb,0=ec,0= 0的前提下, 本节考虑了原行星盘对轨道迁移产生的耗散效应, 通过改变行星盘内的偏心率衰减系数可以调整轨道迁移时标及最终轨道偏心率数值. 令两颗行星初始偏心率均为0,设置不同偏心率衰减系数K, 得到的偏心率平衡值见表3. 为了进一步说明偏心率衰减项K与偏心率最终稳定值的关系, 我们给出偏心率随时间的变化图像. 图3对应的分别是K= 0、100、200、300时的轨道偏心率演化.K= 0即没有添加偏心率衰减效应时,两颗行星的偏心率在平运动共振作用下不断激发, 直到超出观测值.K= 300时, HD 106315c的轨道偏心率受到抑制而无法与HD 106315b形成共振稳定, 且HD 106315b的偏心率快速增大, 系统快速失稳. 根据观测值ec= 0.23、eb= 0.3可知K= 200是当ab,0= 0.4 au、ac,0= 0.8 au、eb,0=ec,0= 0时最接近HD 106315的实际轨道迁移过程的偏心率衰减系数.

表3 偏心率衰减系数及对应的平衡值Table 3 Attenuation coefficient and corresponding equilibrium value of eccentricity

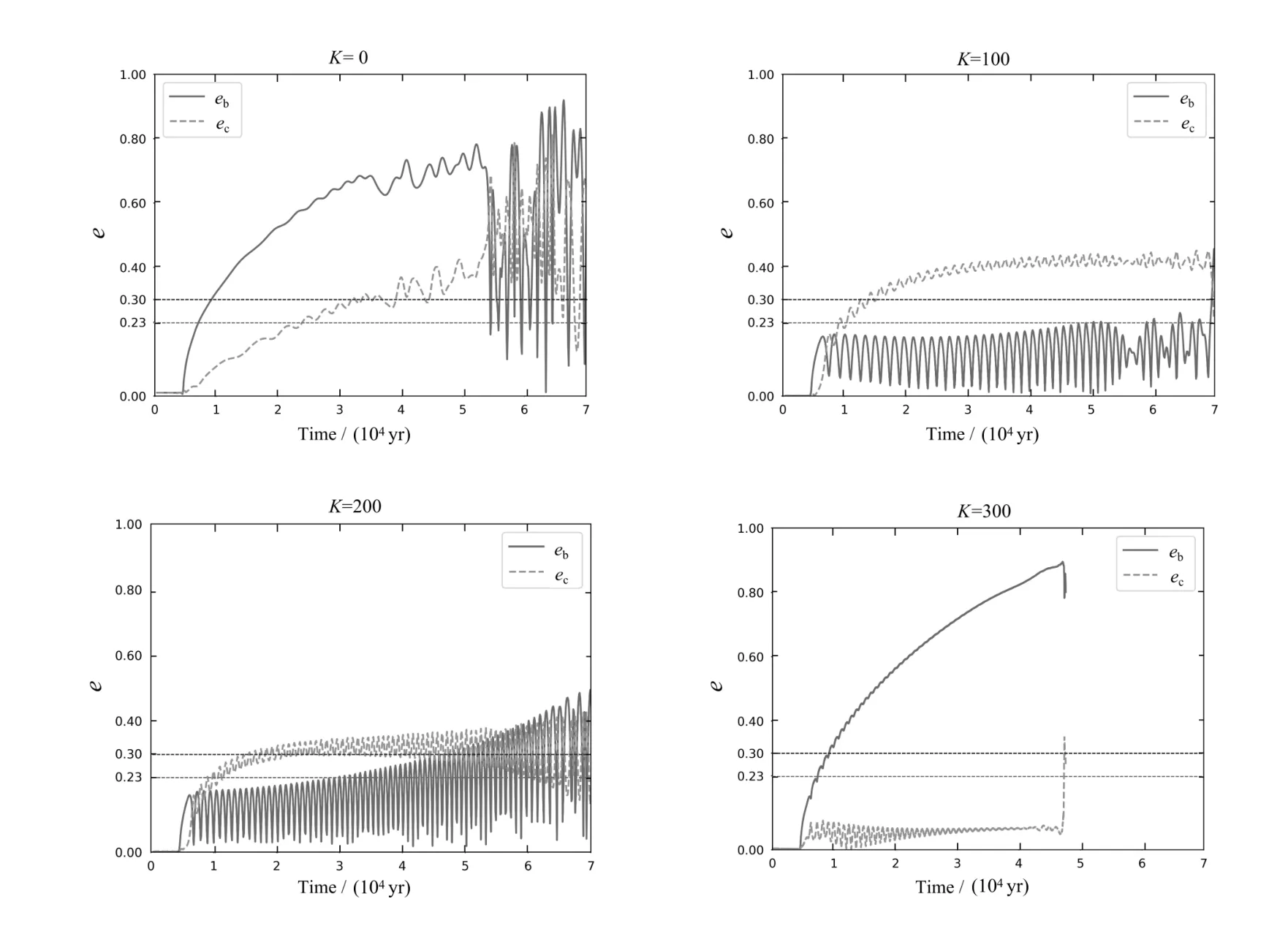
图3 不同偏心率衰减系数下的轨道偏心率演化Fig.3 Orbital eccentricity evolution with different attenuation coefficients of eccentricity

综上, 我们的数值模拟结果给出了HD 106315行星系统的初始轨道半长径和偏心率范围. 假设初始轨道半长径为ab,0= 0.4 au、ac,0= 0.8 au, 两颗行星初始偏心率均为e=0. 随着行星在行星盘内受粘滞力作用,HD 106315c先开始向内迁移,在最初10000 yr, 行星HD 106315b保持在初始轨道位置不变. 随后两颗行星轨道逐渐接近, 在HD 106315c的引力摄动作用以及中央恒星的引力作用下,HD 106315b开始向内迁移,并进入2 : 1平运动共振捕获, 两颗行星的轨道偏心率被激发. 该行星系统轨道半长径和2 : 1平运动共振对应的共振角演化图像见图4.

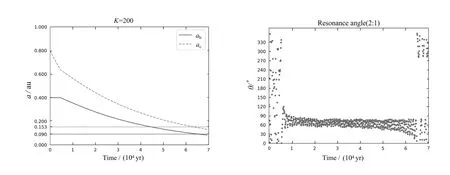
图4 K = 200对应的轨道半长径和共振角演化图像Fig.4 Evolution of semi-major axis and resonance angle with K = 200

4 HD 106315系统的潮汐演化

4.1 一般长期摄动理论修正

根据Kepler空间望远镜观测的系外行星数据, 轨道半长径a >0.2 au的行星轨道偏心率均值在0.3左右, 最大可接近1, 且分布比较均匀. 对于轨道半长径a <0.2 au的系外行星, 其轨道偏心率通常较小(e <0.2)或接近0, 密近轨道的偏心率降低主要是由于主星的潮汐耗散效应[30–32]. 行星轨道偏心率在来自中央恒星的潮汐作用下衰减, 行星公转角动量转化为中央恒星的自旋角动量, 行星偏心率衰减时标主要由行星潮汐耗散系数(tidal dissipation factor)Qp决定.

由第3节的轨道迁移结果可知, HD 106315行星系统中, 较大的轨道偏心率使得系统共振轨道构型不稳定, 考虑轨道迁移停止后的偏心率衰减效应可得到较稳定的共振轨道构型. 且观测时刻系统内气体已耗散殆尽, 无法通过气体耗散作用使系统偏心率有效衰减. HD 106315b的轨道半长径为0.09012 au, 此时主要考虑外轨道HD 106315c的引力摄动作用及中央恒星对HD 106315b的潮汐作用. 系外行星潮汐耗散系数Qp与行星组成和内部结构有关, 在没有精确质量和半径测量数据作为限定条件时, 通常使用估计值. HD 106315b是一颗海王星质量的行星, 根据Gavrilov等[33]的估计, 类海王星的潮汐耗散系数Qp∼105.

与经典单行星系统潮汐理论对比, 双行星系统的潮汐演化模型中添加了中央恒星对内外轨道行星的潮汐力[34−38],ft1和ft2分别是内、外轨道行星受到的来自中央恒星的潮汐力:

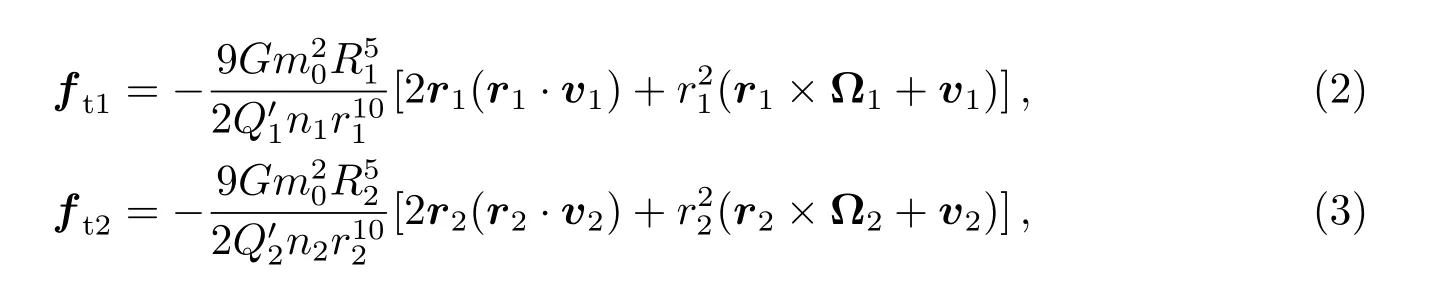
其中G是引力常数,m0为恒星质量,R1,2、n1,2、Q′1,2分别为内外行星的半径、公转速率及修正后的潮汐耗散系数.Q′ ≡3Q/(2k), 其中勒夫数(Love number)k与天体潮汐有效刚性及密度分布有关, 无法精确测定, 此处将实际的行星勒夫数k参数化为3/2,使Q′=Q, 下文统一使用潮汐耗散系数Q.v1= ·r1、v2= ·r2, 分别为内外两颗行星的速度, Ω1,2是内外轨道行星的自转速率.

HD 106315行星系统内两颗行星轨道半长径差值仅为0.06 au, 行星间的引力摄动作用明显, 故此处需考虑引力摄动和潮汐耗散效应耦合作用下的双行星系统的潮汐演化.Laskar等[39]在一般长期摄动理论中添加了相对论和潮汐效应, 修正后的系统长期摄动方程可写为:

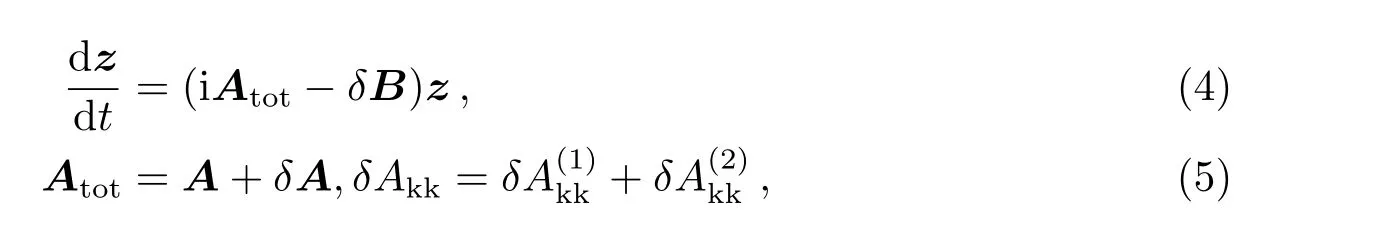
其中,z是行星的位置向量, 行星的运动位置采用复变量表示法:zk=ekeiϖk,ek和ϖk分别是第k颗行星的偏心率和近星点经度,A、δA、δB均为对角矩阵,A是修正前的摄动方程系数矩阵,Atot是添加修正项δA之后的复数部分系数矩阵,δAkk是δA对角线上的元素值,δAkk为相对论效应修正项δA(1)kk和潮汐效应保守项δA(2)kk的叠加,δB为潮汐效应的耗散项. 系统长期摄动方程的解为:

其中,uk(t)表示任意时刻t行星k的位置,γk为考虑耗散项修正定义的系数,gk为矩阵A的本征值,uk(0)为一般长期摄动方程的初解, 可通过行星偏心率初值求解. 复数形式的行星偏心率为uk(t)的线性组合, 线性组合的系数来自Atot与δB矩阵运算得到的复数矩阵.

4.2 潮汐演化理论分析与数值模拟

尽管潮汐耗散时标相比轨道迁移时标长很多, 但在考虑相对论和潮汐效应的长期演化过程中, 潮汐效应保守项和相对论效应会减弱内轨道行星因外轨道行星引力摄动产生的偏心率激发, 从而使行星半长径和偏心率均会缓慢衰减[40–41]. 潮汐演化数值模拟仍然使用MERCURY6算法, 并将4.1节的(2)、(3)式添加到潮汐演化动力学模型中. 本章潮汐演化仅考虑迁移结束后的轨道演化, 轨道半长径初始值设在观测值附近, 且潮汐演化时标远大于轨道迁移时标. 故潮汐演化结果与迁移阶段的初始轨道构型并不直接相关.

首先, 固定初始轨道半长径和轨道偏心率:ab= 0.09012 au、ac= 0.1526 au、eb= 0.4、ec= 0.3, 取行星潮汐耗散系数分别为: 102、103、104、105, 通过改变行星潮汐耗散系数Q观察不同演化时标下两颗行星的潮汐演化结果, 得到的演化结果如图5所示. 该系统的中央恒星HD 106315年龄约为40亿年, 可推测该行星系统剩余寿命约为50–60亿年. 由图5可知, 两颗行星的轨道偏心率衰减时标随潮汐耗散系数的增大而变长,当Q=102、103时,行星的偏心率衰减曲线越过了目前的观测值,而当Q104时,在当前轨道位置上无法通过潮汐效应使偏心率在系统剩余寿命内衰减至观测值eb= 0.3、ec=0.23. 根据前期的研究结果[41–43], 潮汐耗散系数与行星轨道的偏心率衰减时标成反比, 而不影响行星轨道半径演化的最后值. 我们的研究结果也与这些结果一致.

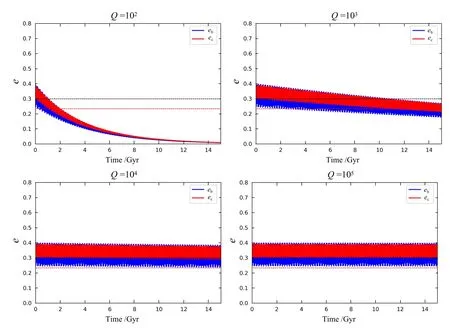
图5 不同潮汐耗散系数下的轨道偏心率演化Fig.5 Orbital eccentricity evolution with different tidal dissipation factors

此外, 为了探究两颗行星的初始偏心率差值是否会对行星潮汐演化产生影响, 假设行星潮汐耗散系数Q=100, 改变初始时刻两颗行星偏心率差值∆e=eb,0−ec,0, 得到的偏心率演化结果如图6所示, 其中ec,0= 0.2, 0.1<∆e <0.4, 图5和图6中的行星偏心率振荡来自两颗行星间的引力摄动作用.

由图6可知, 当∆e较小时, 行星偏心率振荡幅度较小, 随着∆e增大, 两颗行星偏心率振荡幅度均变大, 且初始时刻HD 106315c偏心率受HD 106315b引力摄动激发较明显, 随后波动下降, 反之HD 106315b偏心率不会被HD 106315c激发, 而是直接振荡衰减, 且行星偏心率衰减时标不会随∆e发生变化. 该研究结果可以解释为: 外行星偏心率一定时,随着内行星偏心率变大(∆e变大), 内行星的潮汐衰减效应增强, 在其引力摄动影响下,外行星的轨道衰减也增大. 这与Mardling等[36]的研究结果一致, 导致外行星偏心率衰减的主要原因在于它受到内行星潮汐衰减效应, 而不是其自身受到的潮汐效应.

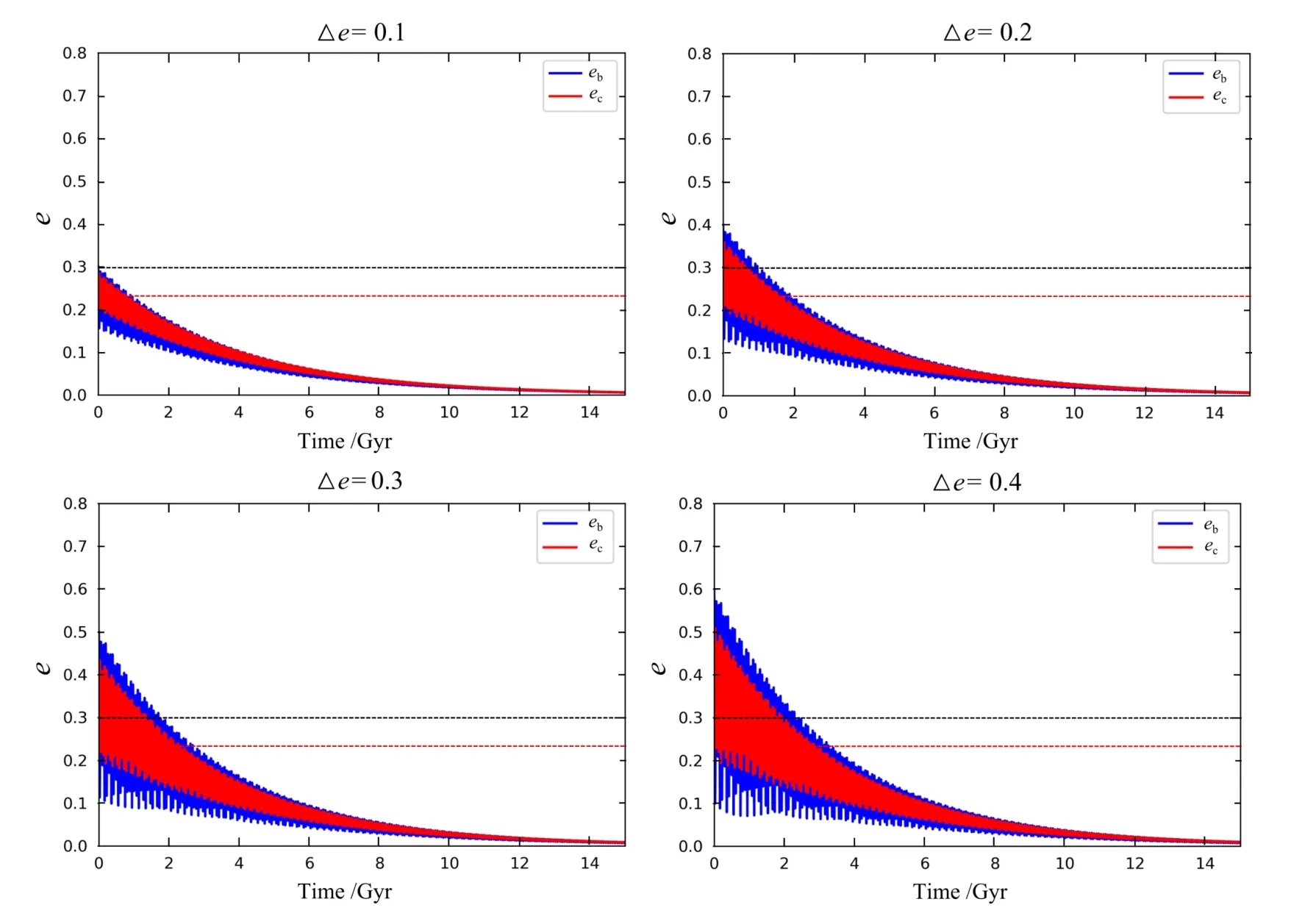
图6 引力摄动和潮汐效应下的行星轨道偏心率演化(理论分析)Fig.6 Orbital eccentricity evolution with perturbation and tidal dissipation (theoretical analysis)

第3节中系统的轨道演化结果表明, HD 106315系统可能经历了2:1共振捕获及脱离共振的过程. 本节给出了HD 106315系统脱离2 : 1共振的可能物理图像: 行星系统在潮汐演化过程中会经历偏心率和轨道半长径的衰减, HD 106315b由于受到更强的潮汐效应会进一步向内迁移, 而HD 106315c受到的潮汐效应较弱, 从而使两颗行星轨道周期比发生变化, 使系统脱离2:1平运动共振构型. 但是潮汐演化数值模拟表明, HD 106315系统内两颗行星潮汐效应作用太弱, 并不会使2:1共振捕获的两颗行星轨道周期比增大至脱离共振.

行星轨道潮汐演化数值模拟结果见图7, 初始轨道参数同图5. 当潮汐耗散系数Q= 100时, 潮汐效应造成的轨道半长径衰减会使系统轨道周期比逐渐增加. HD 106315系统内两颗行星Q103, 潮汐演化过程中轨道周期比几乎没有改变, 验证了中央恒星产生的潮汐效应不是HD 106315系统当前脱离2 : 1平运动共振构型的原因. HD 106315系统可能是由于在原行星盘内轨道迁移初期即进入共振捕获, 且平运动共振激发偏心率时标远小于盘内气体粘滞力对偏心率的衰减时标, 导致HD 106315b偏心率持续受到激发的同时两颗行星轨道距离缩短, 从而脱离2:1平运动共振捕获.

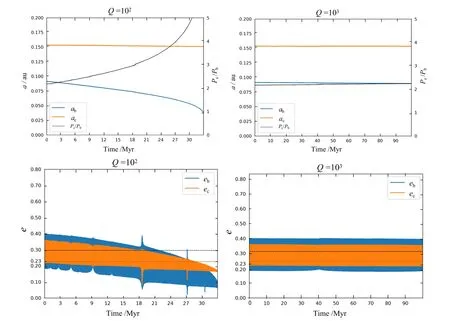
图7 引力摄动和潮汐效应下的行星轨道半长径和偏心率演化(数值模拟)Fig.7 Orbital semi-major axis and eccentricity evolution with perturbation and tidal dissipation(numerical simulation)

5 总结与展望

本文研究了具有大偏心率的热海王星系统HD 106315, 该行星系统目前处于近2 : 1平运动共振轨道构型. 我们研究了在I类轨道迁移和中央恒星的潮汐效应作用下,HD 106315到达当前观测位置以及脱离2 : 1共振的轨道演化机制. 本文结合理论分析和数值模拟方法反演HD 106315行星系统轨道迁移过程, 确定符合观测值的轨道迁移初始参数范围为ab,0∼0.4 au、ac,0∼0.8 au、eb和ec0.03. 行星轨道迁移过程中因原行星盘气体粘滞力产生的偏心率衰减系数K∼200. 系统内两颗行星约在65000 yr演化至目前观测的轨道上.

通过轨道迁移数值模拟发现, HD 106315系统可能经历了2 : 1平运动共振捕获和脱离的过程. 为了解释行星系统脱离2 : 1平运动共振构型的演化机制, 我们讨论了该热海王星系统的潮汐演化. 对比潮汐演化理论分析和数值模拟结果, 发现当行星潮汐耗散系数Q= 100时, 潮汐效应造成的轨道半长径衰减会使系统轨道周期比发生变化, 可能是系统脱离共振构型的原因. HD 106315系统内两颗行星Q103, 来自中央恒星的潮汐效应并不会使行星系统产生明显的偏心率和轨道半长径衰减, 中央恒星产生的潮汐效应不是HD 106315系统当前脱离2 : 1平运动共振构型的原因. 由于Crossfield等[6]根据恒星HD 106315的视向速度数据推测该系统内可能存在第3颗行星d, 且该行星质量45M⊕, 而较大质量的行星d的存在可能使内部轨道的行星b和c进入或脱离特定的共振构型[44].

在对HD 106315行星系统进行初始半长轴筛选时发现,ab,00.8 au、ac,01.6 au时对应的行星轨道迁移有形成3 : 2平运动共振和4 : 3平运动共振的趋势, 这是由于随着相邻轨道上的行星距离缩小导致的轨道周期比下降. 但是潮汐演化过程中, 轨道周期比却呈上升趋势. 所以在未来的工作中, 我们将继续关注在行星轨道迁移和潮汐共同作用下, 热海王星行星系统由2:1平运动共振转化为其他共振的关键影响因素和限制条件以及大偏心率密近轨道上的热海王星系统的稳定性和潮汐演化时标. 同时, 密近轨道上的热海王星也是系外行星大气的重要研究目标, 随着系外行星大气观测方法和演化理论的发展[45], 热海王星大气特性研究也将进一步促进系外行星的形成和演化理论的发展.