基于分位数回归和哑变量模型的大兴安岭兴安落叶松树高-胸径模型

王君杰，夏宛琦，姜立春

（东北林业大学 林学院，黑龙江 哈尔滨 150040）

树高-胸径模型在计算树干材积、出材率表编制、生长和收获模型、森林资源调查、立地质量评价、生物量和碳储量研究等方面有着广泛的应用[1-5]，目前，树高-胸径模型的模型形式主要有非线性模型和混合效应模型。非线性模型采用普通最小二乘法（OLS）得到参数估计[6-7]，但只能得到树高的平均预测。当数据来自较大区域，即立地条件不同时，总体使用最小二乘法对一些区域可能产生较大误差。此外，最小二乘法假定模型误差服从独立正态分布，当违背这种假设时，得到的参数估计不可靠。混合效应模型同时考虑固定效应参数和随机效应参数，使用固定效应参数可以得到树高的平均预测，如果能够计算随机效应参数值就可以进行个体预测[8-9]。个体预测需要进行二次抽样校正随机参数。二次抽样对于小尺度是可行的，但对于大尺度区域进行二次抽样会大大增加调查成本，且会增大树高测量的误差，在实际应用时限制了混合模型个体预测的应用，而混合模型总体平均预测效果有时不如传统的最小二乘法[10-11]。此外混合效应模型应用数据条件必须是分组数据或纵向数据，如果数据没有这样的信息，如结合森林采伐获得的伐倒木实测树高和胸径数据，没有样地信息，无法应用混合效应模型进行分析，因此不能进行混合效应树高-胸径模型的构建。

分位数回归（Quantile regression）由Koenker和Bassett[12]提出，它可以给出一组用来描述响应变量的分位数回归曲线。不同回归曲线具有各种形状，可以灵活地反映数据的变化规律。近年来，分位数回归方法在林业上已经用于构建和研究自稀疏边界线模型[13]、胸径百分位模型[14]、胸径生长模型[15]、削度方程[16]和最大密度线模型[17]等。

哑变量（Dummy variable）模型是将一个分类变量引入基本模型中，仅拟合一个模型就可以得到不同分类变量模型的参数估计值。在林业中常用于不同区域模型的构建，并与混合效应模型等方法共同使用，提高模型精度[9,18]。已有很多学者对哑变量方法与线性混合效应模型[19]、非线性混合效应模型[20-21]等其他方法进行比较，但与分位数回归模型的比较还未见报道。

本研究以大兴安岭4个区域的兴安落叶松Larix gmelinii为研究对象，采用分位数回归方法和哑变量方法构建各区域的树高-胸径模型，确定各区域树高-胸径模型的回归系数，然后对分位数回归模型、哑变量模型和传统的基本模型进行详细的对比分析，为林业树高-胸径模型的构建提供新的思路和方法。

1 研究区概况

大兴安岭地区是我国天然林和重点国有林的主要分布地区之一，属大陆寒温带季风性针叶林气候，平均海拔573 m，年平均气温-2～4 ℃，年降水量450 mm左右。物种资源丰富，主要树种为兴安落叶松，其次是樟子松Pinus sylvestrislvar.mongouca、云杉Picea koraiensis、白桦Berula platypgylla等。本区属高纬度山地，地势西高东低，主要土壤类型为棕色针叶林土、暗棕壤、暗色草甸土和沼泽土等。地貌基本属于低山、丘陵地貌，地形起伏不大。全区河谷宽阔，江河网布，水资源丰富，存在大量的沼泽地和草甸地貌，年径流量达149亿m3以上。

根据张万儒等[22]的方法，将研究地区划分为4个区域：漠河、图强和阿木尔划分为区域1（西北）；塔河、十八站和韩家园划分为区域2（东北）；松岭、加格达奇划分为区域3（中部）；呼中、新林林场划分为区域4（南部）。分区情况见图1。在4个区域实测了2 411株兴安落叶松伐倒木的胸径和树高。为了使数据具有代表性，每个区域树高和胸径数据都尽量接近正态分布。采用随机的方法将每个区域的数据分成建模数据（80%）和检验数据（20%），即建模样本数据共1 933对，检验样本数据共478对。各区域的建模样本和检验样本数据统计量基本情况见表1。

2 研究方法

2.1 基本模型

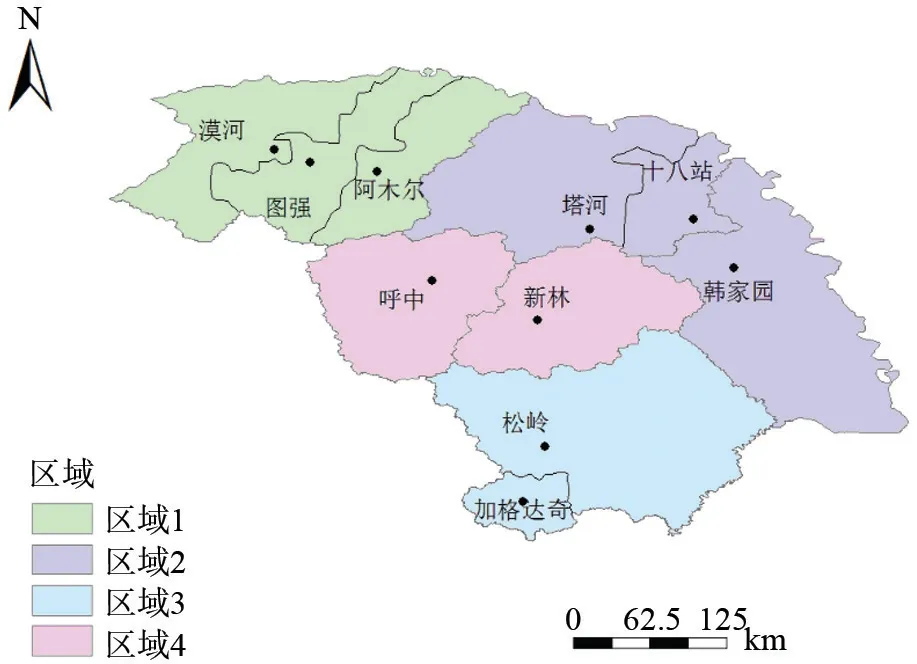
图1 研究区域分区情况Fig.1 Partition of the study area

选取国内外林业上广泛应用的12个树高-胸 径 方 程：Weibull方 程、Schumacher方 程、Richards方程、Korf方程、Loetsh方程、Curtis方程、Mitscherlich方程、唐守正方程、Sibbesen方程、Wykoff方程、Hossfeld方程、Ratkowsky方程[3,23]。初步分析表明Richards方程表现了较好的拟合效果，因此本研究选取Richards方程作为基本模型，模型形式如下：

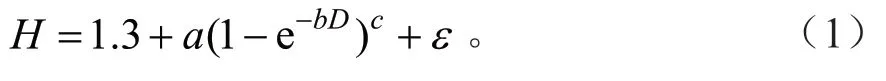
式中：H为树高；D为胸径；a、b、c为模型参数；ε为误差项。

2.2 分位数回归

分位数回归（Quantile regression）利用自变量的多个分位数得到因变量条件分布的相应分位数方程，可以捕捉分布的尾部特征，对条件均值以外的预测非常有效[24]。当自变量对不同部分的因变量的分布产生不同的影响时，例如出现左偏或右偏的情况时，更加全面地刻画分布的特征，从而得到全面的分析[25]。

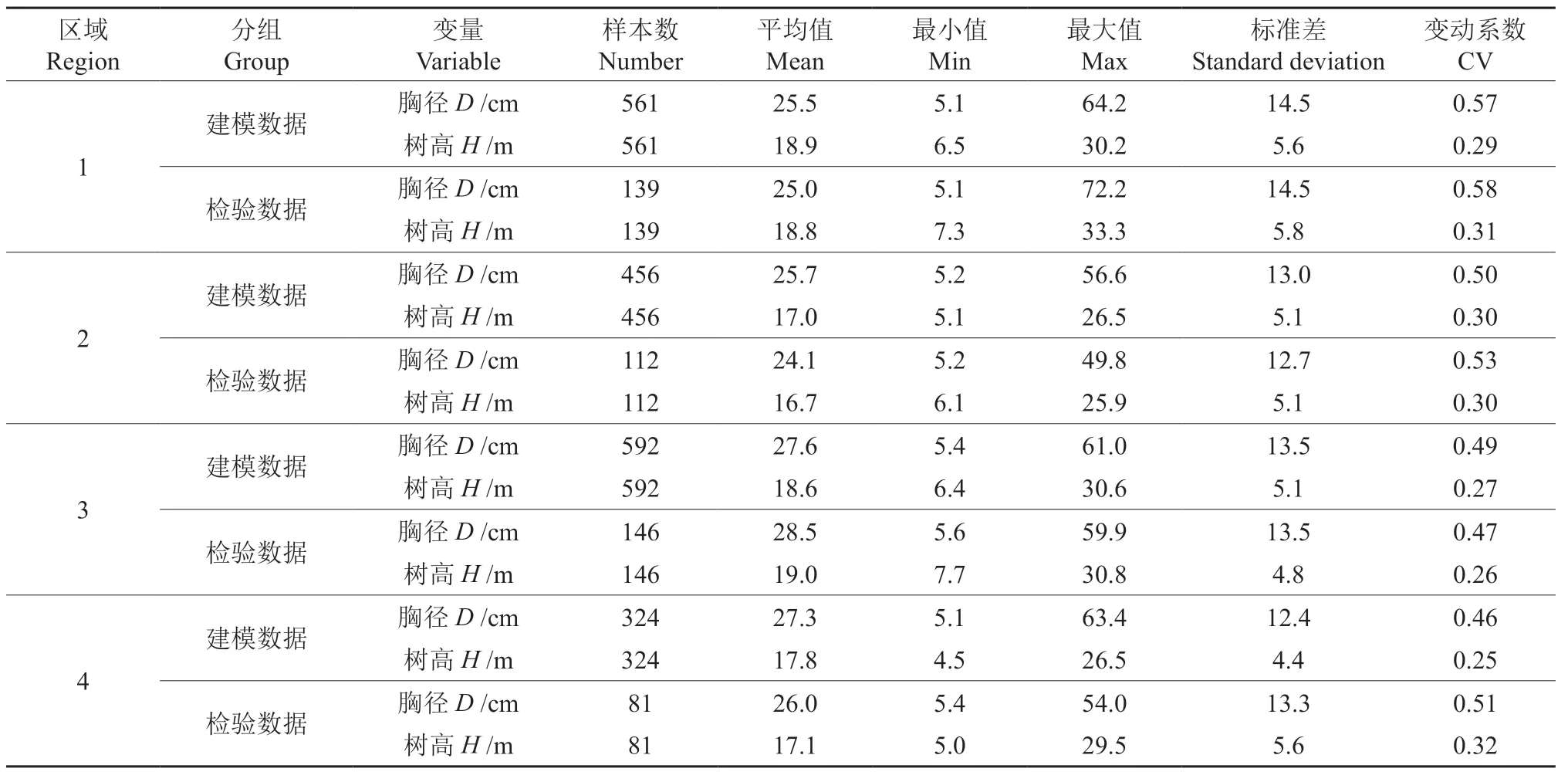
表1 兴安落叶松样本统计量Table 1 Summary statistics for sample trees of Larix gmelinii

基于Richards方程，其9个分位数（τ=0.1, 0.2,0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9）树高-胸径模型形式如下：

式中：Hτ是第τ个分位数的树高预测值；aτ、bτ、cτ是第τ个分位数模型的参数，其他参数定义同上。

分位数模型中第τ个分位数模型的参数估计可以通过最小化残差绝对值的非对称损失函数来估计[13]，如式（3）所示：

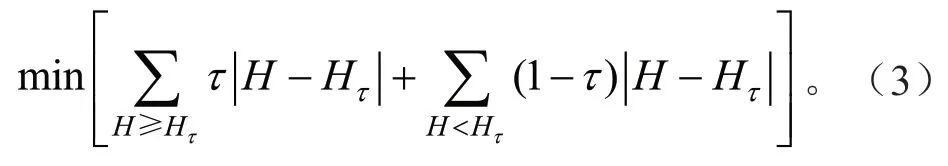
不同分位数模型拟合具体采用SAS软件中的非线性规划（NLP）模块计算不同分位数τ上的树高-胸径方程的参数估计。

2.3 哑变量模型

哑变量（Dummy variable）模型是在基础模型中引入一个定性变量，将不同区域的生长模型整合成一个模型，进行参数估计时仅对哑变量模型进行拟合即可得到各区域的参数估计值，既减少了工作量，又解决了不同区域单独建立模型所造成的整体和分量之间不相容的问题[26]。哑变量法不同于最小二乘法将所有参数都视为全局参数，也不同于混合模型方法将模型参数视为适用于总体的固定参数和适用于个体的随机参数的和，它把个体参数看作是固定的，但在不同的个体之间却是不同的[20]，Wang等[27]称之为固定个体效应。

Richards方程在不同区域都表现了显著的不同，因此本研究也构建了不同区域的哑变量树高-胸径模型，基于Richards方程的哑变量模型如下：

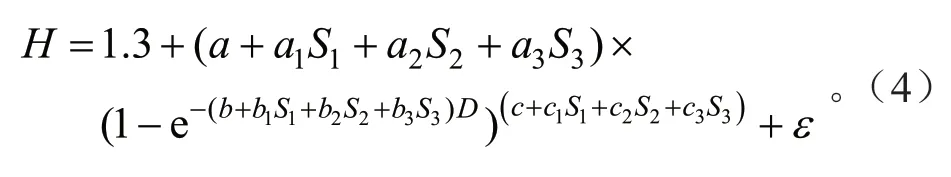
式中：a1、a2、a3、b1、b2、b3、c1、c2、c3是与区域有关的参数值；S1、S2、S3为哑变量，其他参数定义同上。当区域为区域1时，S1=1，而S2、S3为0，依次类推。当区域为区域4时，S1、S2、S3都为0。

采用非线性额外平方和法比较不同区域间的差异[28]，如果没有显著不同，则各区域之间可以共用一套参数。该方法需要拟合无限制模型（Full model）和限制模型（Reduced model）。无限制模型对不同区域有不同的一组参数值，限制模型对所有区域有一组相同的参数值。在本文中，无限制模型即加入哑变量的模型，限制模型即基本模型（1）。采用F检验进行比较，F值计算如下：

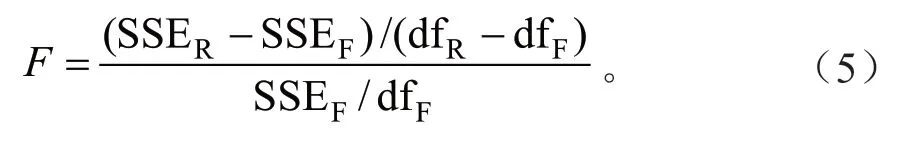
式中：SSEF为无限制模型的误差平方和；SSER为限制模型的误差平方和；dfF为无限制模型的自由度；dfR为限制模型的自由度。

2.4 模型评价和检验指标

拟合结果采用平均绝对误差（MAE）、均方根误差（RMSE）、确定系数（R2）和赤池信息量（AIC）、贝叶斯信息量（BIC）来对比不同模型。检验结果采用平均绝对误差（MAE）、平均预测误差百分比（MPE）、平均绝对百分比误差（MAPE）、均方根百分比误差（RMSPE）进行检验。

3 结果与分析

3.1 模型的参数估计

选择9个不同的分位点（τ=0.1, 0.2, 0.3, 0.4, 0.5,0.6, 0.7, 0.8, 0.9），利用SAS统计软件的非线性规划PROC NLP模块对分位数模型（2）进行非线性分位数回归拟合。利用SAS软件中的PROC NLIN过程对哑变量模型（4）和基本模型（1）进行拟合，得到各方法模型的参数估计值，结果见表2。由表2可以看出，基于不同分位数的参数估计各不相同，整体有一定的趋势走向。随着分位点τ的增大，渐近线参数a逐渐增加，斜率参数b先增加后减小，形状参数c逐渐变小，这反映出在不同分位数处的树高曲线的变化规律。基于哑变量方法的各区域参数也各不相同，且不同于基本模型求出的参数。

表3显示了整个大兴安岭地区和4个划分区域之间树高-胸径模型差异的测试结果。式（5）用来检验使用全部数据的限制模型是否足以满足4个划分区域的需要。从表3可以看出，使用全部数据的限制模型不足以描述4个划分区域的树高-胸径关系（F=49.32，P=0）。然后利用4个区域两两进行检验：将4个区域的数据两两进行合并，分别构建成对区域的含有哑变量的无限制模型（哑变量个数都为1），对成对区域的无限制模型和限制模型进行拟合，并利用式（5）计算F值及相应的P值。除区域2和区域4外，其他5个成对区域P值都显著，表明其他5个成对区域有显著不同；而区域2和区域4差异不显著（F=1.27，P=0.284 4），说明区域2和区域4的树木长势没有明显区别，可以利用同一个模型进行拟合。

表2 基于不同方法的树高-胸径模型参数估计†Table 2 Parameter estimates of height-diameter models based on different methods

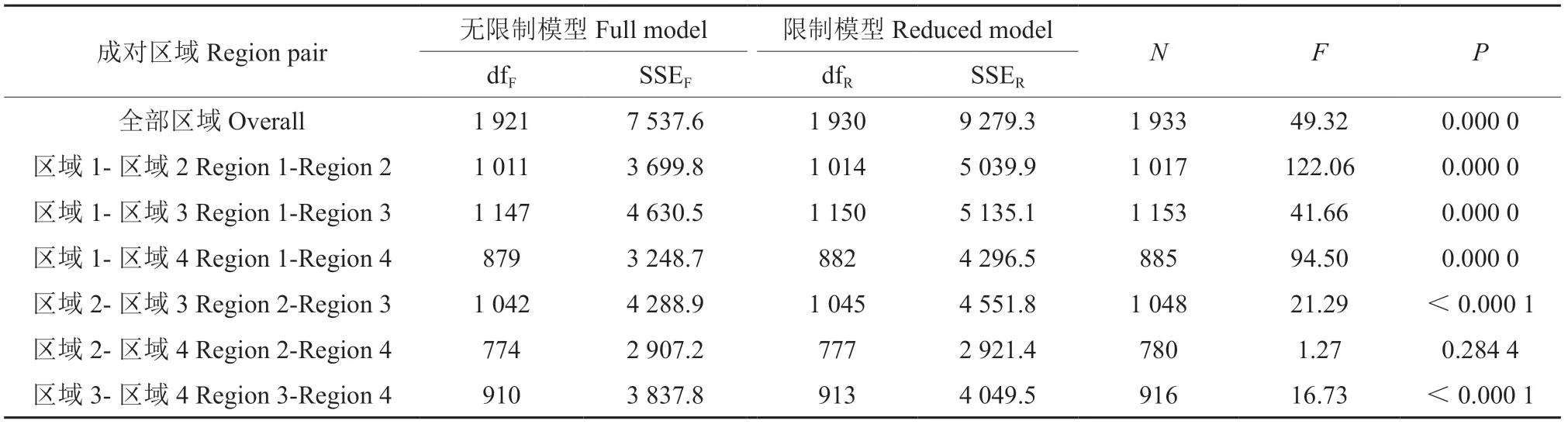
表3 不同区域模型对比F检验Table 3 F-test for models for different regions

为了更直观地分析分位数模型模拟树高曲线的趋势，利用拟合数据绘制不同分位数的树高曲线（图2），其中A为基本模型，B为中位数模型（τ=0.5），C为3个分位数组合（τ=0.1,0.5,0.9），D为5个分位数组合（τ=0.3,0.4,0.5,0.6,0.7），E为7个分位数组合（τ=0.1,0.2,0.3,0.5,0.7,0.8,0.9），F为9个分位数组合（τ=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9）。由图2A—B可知，中位数曲线与基本模型曲线十分接近，说明拟合数据近似正态分布。而从图2B—F可以看出，各分位数曲线都在树高观测值中穿过，使得观测值插在两个相邻的分位数曲线中。无论是数据密集的小径阶，还是数据分布稀疏的大径阶，分位数回归方法可以清楚地描述树高曲线的变化规律，这也说明不同分位数曲线能够表达不同区域不同立地条件的树高曲线变化。

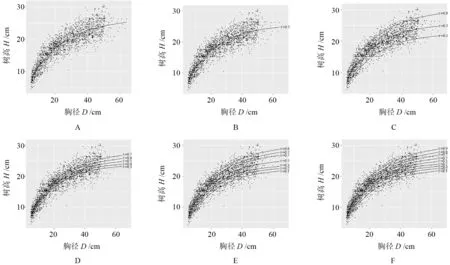
图2 不同分位数兴安落叶松树高-胸径曲线模拟Fig.2 Height-diameter models simulation of Larix gmelinii based on base model, median model and different quantile groups

3.2 模型拟合结果总体评价

一组QR模型可以用来模拟树高-胸径关系，并检验不同大小的树的分位数之间的差异[9]。因此可以根据拟合统计量选择出各区域所对应的最优分位数模型，进而比较各区域树木生长的差异。将表2中的参数估计值代入Richards方程中，计算各树高-胸径模型的拟合统计量，结果见表4。由表4可看出，各个区域都可以根据拟合统计量从其9个分位数模型中选出一个最优的分位数模型，即在所有分位数模型中拥有最小的MAE、RMSE、AIC、BIC值和最大的R2值，4个区域所对应的最优分位数模型分别为τ=0.7、τ=0.3、τ=0.5和τ=0.3。各区最优分位数模型与各区哑变量模型拟合结果差异不大，除区域3外，这2种方法均优于基本模型。区域3最优分位数模型为中位数模型，即τ=0.5，且基本模型的拟合效果也较好，说明区域3的树高曲线与总体拟合数据的树高曲线趋势比较接近，适用于代表平均水平的基本模型。区域3的基本模型与其最优分位数模型（τ=0.5）的AIC、BIC值相差很小（ΔAIC=3.116、ΔBIC=3.115），几乎可以认为是同一模型。而区域1、2、4如果仅用基本模型进行估计误差会较大。区域1的最优分位数模型为τ=0.7，说明区域1树木长势分布偏高，立地条件较好。区域2、4的最优分位数模型都为τ=0.3，说明这2个区域的树木长势分布相似，这与F检验时得到的结论一致，即区域2和区域4的树木长势没有明显区别，可以利用同一个模型进行拟合。且与其他2个区域相比，区域2、4都出现长势偏低的趋势，也说明这2个区域的立地条件相对较差。

表4 基于不同方法的树高-胸径模型拟合统计量†Table 4 Goodness-of-fit statistics of height-diameter models based on different methods

3.3 模型检验

为了更好地评价树高-胸径模型的预测能力，模型检验至关重要。利用检验数据对3种方法构建的树高-胸径模型进行检验，结果见表5。就本文中构建的3种模型来看，区域1、3、4的最优分位数回归模型都要优于哑变量模型，且这2种模型都优于基本模型。虽然区域2的哑变量模型要优于最优分位数模型，但区域2的哑变量模型没有通过正态性检验（P=0.028 6），则区域2的最优模型仍然为τ=0.3时的分位数模型。因此，4个区域的最优树高-胸径模型如下：

区域1：

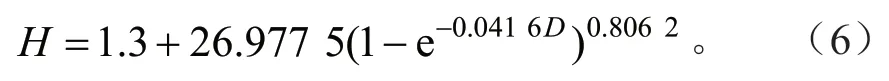
区域2和区域4：

区域3：

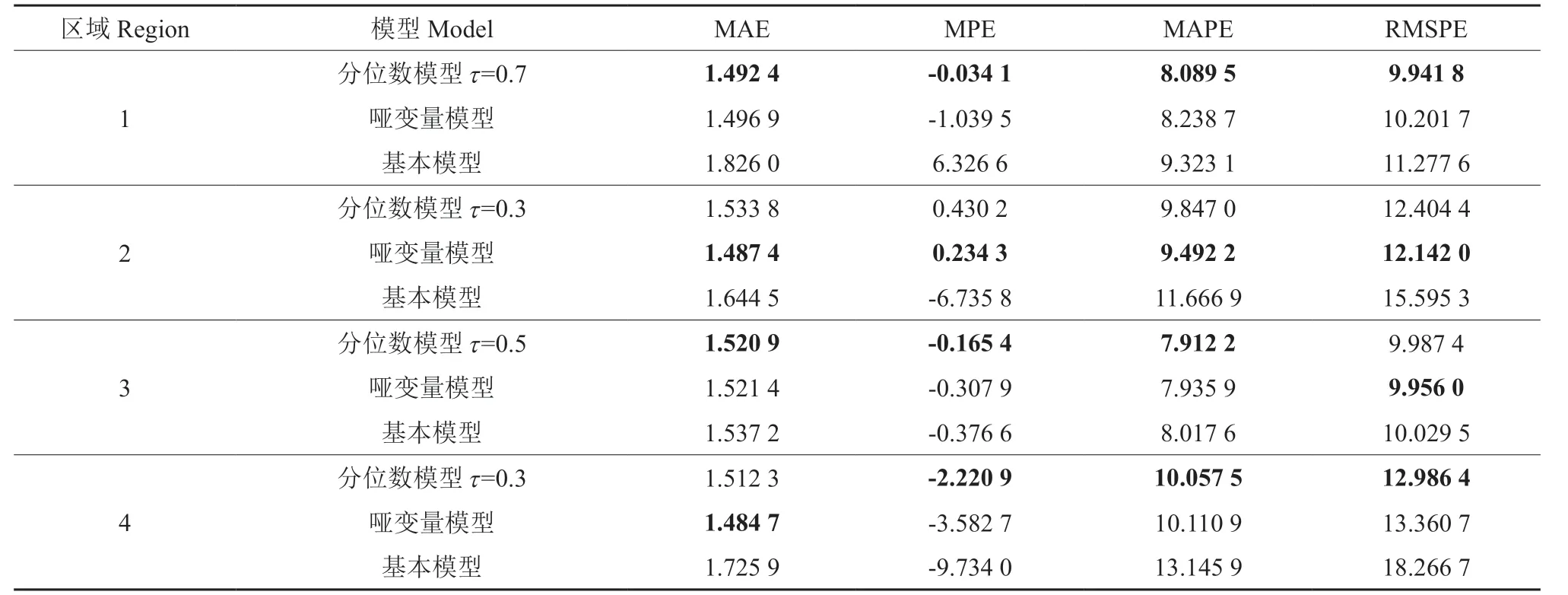
表5 不同方法的树高-胸径模型独立性检验†Table 5 Validation statistics for height-diameter models based on different methods

3.4 不同树高-胸径模型应用模拟

为了更直观地比较3个模型的预测效果，利用检验数据进行不同模型的树高曲线模拟。图3给出了各区域对应的最优分位数模型、哑变量模型、基本模型的兴安落叶松树高模拟曲线。由图3可以看出，在4个区域中，最优分位数模型与哑变量模型在各区域拟合曲线十分接近，趋势也几乎相同，都反映了数据的平均变化趋势。基本模型在区域1、2和4偏差较大，而在区域3与最优分位数模型和哑变量模型模拟曲线比较接近，这也说明区域3的数据分布近似于总体数据的分布。

4 结论与讨论

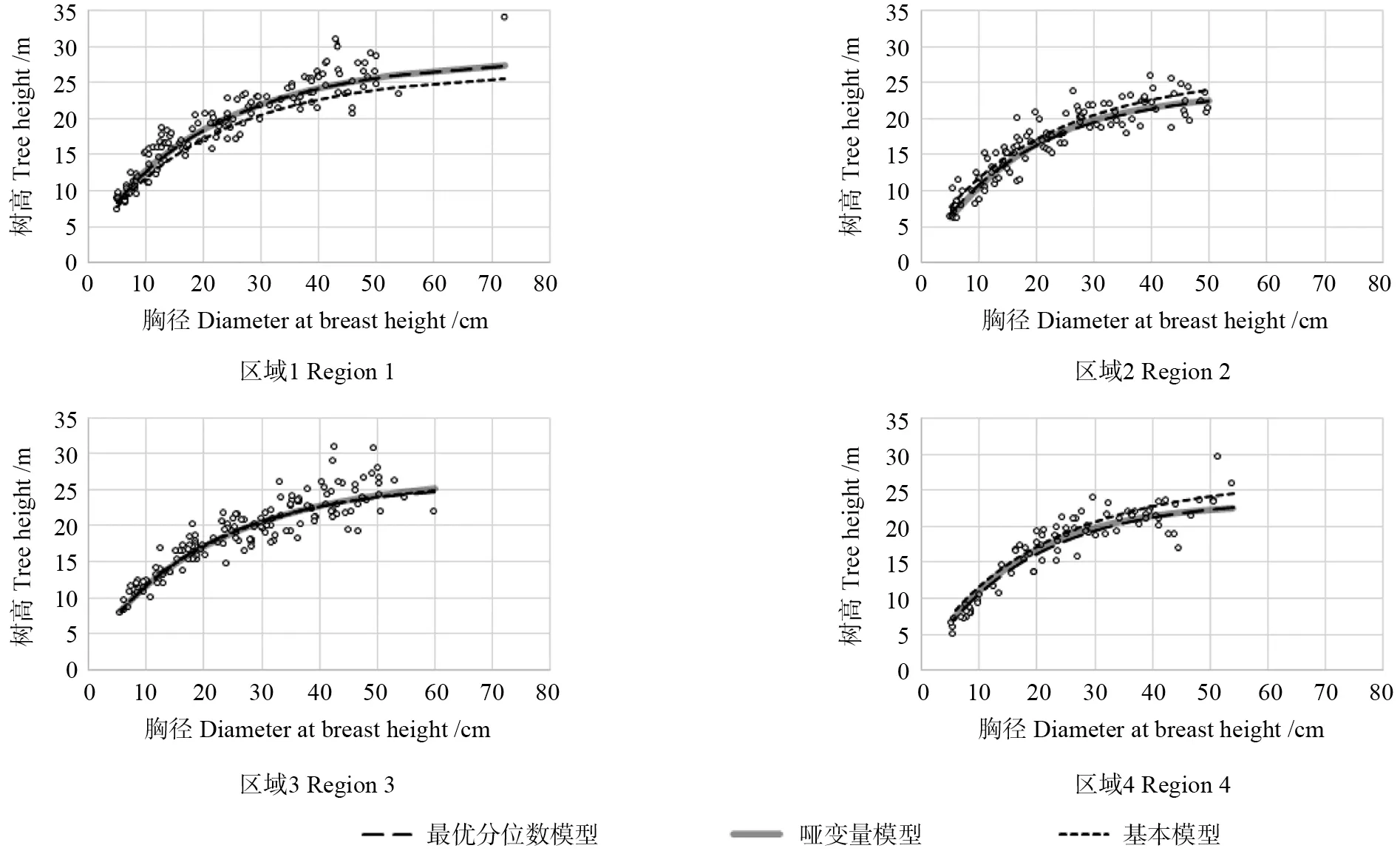
图3 不同方法的树高-胸径曲线预测模拟Fig.3 The simulation of height-diameter models based on different methods

准确的树高预测对于估算树木材积、评价立地指数、描述林分的发展和演替至关重要[28]。建立大尺度范围的林木模型是林业建模中的一项重要工作，但随着方程通用性的提高，用于局部地区的误差也会增大[29]，因此迫切地需要了解不同小区域之间的差异。本研究按照地理方位，将大兴安岭地区划分为西北（区域1）、东北（区域2）、中部（区域3）和南部（区域4）4个区域，引入哑变量建立大兴安岭地区4个区域的无限制模型，并与整体区域的限制模型进行F检验，发现限制模型不足以描述4个区域的树高-胸径关系。对两两区域之间的差异进行比较，发现东北（区域2）和南部（区域4）之间没有明显差别，可以共用同一模型。其他5对区域都有显著不同，说明大兴安岭东北部和南部的树木长势十分相似，当地的环境条件，如气候、土壤和水源等可能非常相似，需要进一步调查研究。

树高-胸径模型拟合时最常使用的方法就是最小二乘法。赖巧玲等[30]发现最小二乘法对异常数据比较敏感，因而当样本量不够大时，最小二乘法得到的参数估计不够稳定。Calama等[2]也发现，当数据有相关性时使用普通最小二乘回归法会导致置信区间的偏差。与最小二乘法相比，分位数方法具有很多优势[31]：适合异方差模型，不需要对模型干扰项做假定，不易受到异常值的影响，能更全面地刻画条件分布的特征等。Zang等[9]构建了落叶松人工林的树高-胸径基本模型和分位数模型，但并没有对两者进行比较。本研究利用拟合数据进行9个分位点（τ=0.1, 0.2, 0.3, 0.4, 0.5, 0.6,0.7, 0.8, 0.9）的分位数模型的拟合，发现无论是数据密集与否，分位数回归都可以清楚地描述树高曲线的变化规律。4个区域各自的最优分位数模型和哑变量模型没有显著差异，可以根据实际情况进行选择：若数据量足够大，满足独立、正态、等方差的假设，这两种方法都可以使用；若数据不满足基本假设，或数据量较少时，建议使用分位数模型。尽管区域2的拟合统计量显示哑变量模型优于最优分位数模型，但区域2数据不符合正态分布，因此认为区域2的最优模型为分位数模型。此外，根据各区域得到的最优分位数模型的分位点的不同，也可以得到不同区域间树木长势的信息。区域1的最优分位数模型所对应的分位数是τ=0.7，则相对于其他3个区域，当树木具有相同的胸径时，区域1所对应的树高偏高，说明区域1的立地条件、水源、光照比较适合树木的生长。区域2和区域4的最优分位数模型所对应的分位数都是τ=0.3，说明2个区域的树木长势相似，环境条件可能十分相似，这一点可以从区域2和区域4的限制模型和非限制模型的比较中得到相同的结论。区域3的最优分位数模型所对应的分位数是τ=0.5，且拟合效果与基本模型相似，说明区域3的数据分布与总体数据的分布十分相似，可以利用基本模型直接拟合。

本研究采用林业上广泛应用的Richards生长方程构建了大兴安岭不同区域的兴安落叶松树高-胸径模型，对比了分位数模型、哑变量模型和基本模型的拟合效果和预测能力。结果表明：各个区域都有其对应的最优分位数模型，且各区域最优分位数模型与哑变量模型拟合结果差异不大，并且都优于基本模型。从预测能力来看，最优分位数模型要略优于哑变量模型，且都优于基本模型。利用哑变量模型和分位数模型可以了解不同区域之间的差异，为森林资源管理者和规划者提供更准确的树木生长发育信息。在进行方法选择时，可以根据数据特征进行选择。本研究所使用的是伐倒木实测数据，由于样本数量有限，只比较了树高-胸径模型的平均预测，随着数据的积累，可以将分位数模型、组合分位数模型和混合效应模型进行比较。