中考数学方案的最优设计题型简析
2020-09-27 23:01李娟刘燚
教育周报·教研版 2020年33期
关键词:中考数学
李娟 刘燚


摘要:中考数学方案的最优设计试题的基本类型有一次函数最值型、二次函数最值型。
关键词:中考数学 最优设计 简析
最优即最佳、最好。方案的最优即是生活中的方案达到最省、最大利润等。《义务教育数学课程标准(2011年版)》中多次提到让学生学会在具体的情境中从数学的角度发现问题,并运用数学知识和方法等解决简单的实际问题。其中通过用代数式、方程、不等式、函数等表述数量关系的过程,建立数学模型,再利用函数的最值来确定方案的最优答案。研究历年中考试题,不难发现中考试题中频繁出现该类题型。中考数学方案的最优设计试题的基本类型有一次函数最值型、二次函数最值型。
一、一次函数最值型
中考问题一次函数最值型试题常以生活中的具体情境为背景,问题常涉及多个小问,前1-2小问利用方程(组)、不等式(组)求出相关数据及确定方案总数,最后一问需列出一次函数及结合求出的自变量的取值范围利用它的增减性确定最大值(最小值)从而找到方案的最优。在这过程中有利于学生阅读理解、数学建模、分析和解决问题能力的提高。一次函数最值型常见两种形式:根据一次函数性质确定最优方案、比较函数值确定最优方案。
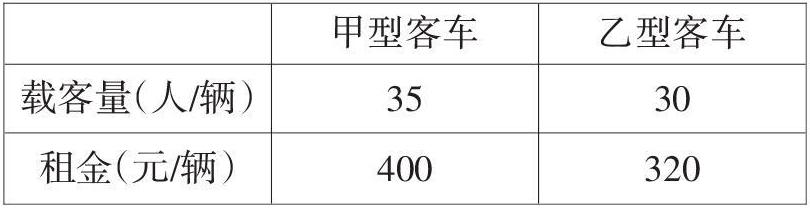
例1 (2019 湖北荆州 第23题)荆州市某中学组织八年级全体学生前往松滋洈水研学基地开展研学活动.在此次活动中,若每位老师带队14名学生,则还剩10名学生没老师带;若每位老师带队15名学生,就有一位老师少带6名学生,现有甲、乙两种大型客车,它们的载客量和租金如表1所示:
学校计划此次研学活动的租金总费用不超过 3000 元,为安全起见,每辆客车上至少要有 2 名老师.
(1)略
(2)略
(3)學校共有几种租车方案?最少租车费用是多少?
猜你喜欢
中学教学参考·理科版(2017年2期)2017-04-05
学周刊(2017年6期)2017-03-30
教育界·上旬(2016年9期)2017-03-17
新教育时代·教师版(2016年46期)2017-03-02
文理导航(2016年35期)2017-02-08
考试周刊(2017年7期)2017-02-06
新教育时代·教师版(2016年26期)2016-12-06
中学课程辅导·教师通讯(2015年11期)2015-08-24

