着眼数学建模 厘清解题思路——从几何图形背景应用题谈高三复习教学

蒋 昊

(江苏省南通市小海中学，226015)

作为核心素养之一的“数学建模”,是对现实问题进行数学抽象,用数学语言表达问题，用数学方法构建模型解决问题的素养．在现实情境的基础上,构建数学模型,发展“四能”,达到“三会”．本文从一道高考数学模拟题入手,尝试阐述几何图形背景这类应用题教学上的实践和思考.

一、典例讲解,积累活动经验

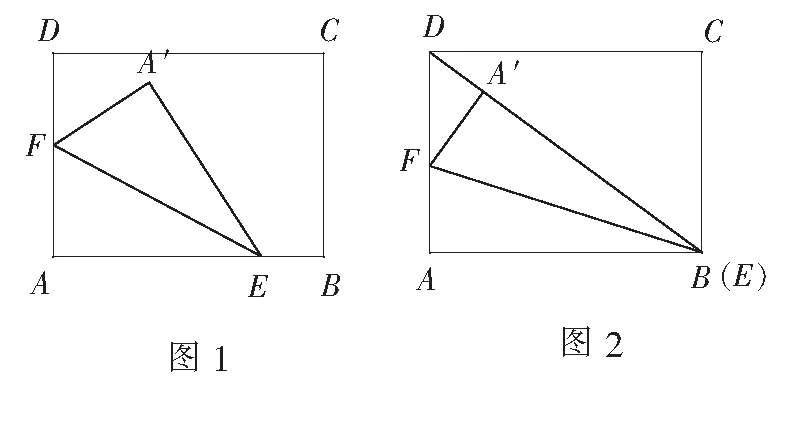
例1(2019江苏省南通市第三次调研测试)南通风筝是江苏传统手工艺品之一.现用一张长2 m,宽1.5 m的长方形牛皮纸ABCD裁剪风筝面.裁剪方法如下:分别在边AB,AD上取点E,F,将三角形AEF沿直线EF翻折到A′EF处,点A′落在牛皮纸上,沿A′E,A′F裁剪并展开,得到风筝面AEA′F,如图1.

(1)若点E恰好与点B重合,且点A′在BD上,如图2,求风筝面ABA′F的面积;

通常解题流程分为:“审题—建模—解模—还原”四个步骤．其中“建模”和“解模”是解决应用题最为关键的两个环节,也是学生最无从入手的部分．例1是以江苏南通传统手工艺品风筝为问题情境,以图形为背景,以求值为目的的应用问题．本道题的第(1)问难度小,学生操作解决较为容易,文中不再剖析．而第(2)问是属于典型的“动态图形求最值问题”,相较第(1)问的静态求值问题难度较大．本课的教学重点即为帮助学生解决“建模”和“解模”的困难.

二、追根溯源,寻找“动”因建模

在学生充分阅读题目,理解题意后,笔者针对第(2)问设计了下列一组问题:

问题1为什么点A′到AB会有距离的最大值?这是一个动态问题还是一个静态问题?

问题2追根溯源,导致A′到AB距离变化的“源头”是什么?

问题3对于变化的“源头”,能有办法刻画吗?

设计意图设计这组问题的目的是让学生明了本题是个动态求值问题,A′到AB的距离是在变化的,因而才会涉及求距离最值问题．进而引导学生探究发现距离变化的“源头”．在课堂教学中，有学生提出“是因为点A′位置的变化才导致A′到AB的距离变化,所以源头是点A′”．此时，教师进一步引导学生思考如何引入参数刻画动点A′,建系设点A′的坐标为(x0,y0)的想法也就自然而然地迸发出来了,我们需要解决的就是y0的最大值．至此就把一道实际的应用问题转化为解析几何模型.

也有学生提出：“是因为∠AEF的变化才导致A′到AB的距离变化,所以源头是∠AEF”．此时教师则可以引导学生考虑设∠AEF=θ,将参数θ引入进来,思考能否用θ来表示点A′到AB的距离,也就是将这道实际的应用问题转化为三角模型处理.

三、紧扣图形,紧抓“定”性解模

问题4题中要求对纸张进行翻折,就数学本质而言这是哪类问题?

问题5前面已经分析过,“翻折”是个动态过程,在此过程中有固定不变的关系吗?

设计意图将实际问题转化为数学模型之后,教学中需要考虑如何帮助学生实现“解模”．在解模过程中,要引导学生紧扣图形,尽管是动态图形,还是要能够“动中取静”．引导学生在动态过程中,寻找到固定的性质,并以此为抓手突破解模．本题的“抓手”在于这是一个翻折问题,就其本质而言是一个“轴对称”问题,也可以理解为是一个“全等变换”问题．由此衍生出来的性质特征是能帮助学生解模的．设计这组问题能让学生明确本题动态变换的实质,基于不同角度观察都能发现固定不变的关系．从学生建立的解几模型出发,在翻折过程中点A与点A′关于直线EF对称是恒定不变的;从学生建立的三角模型出发,在翻折过程中AEF≌A′EF,即∠AEF=∠A′EF=θ是恒定不变的.

基于上述两个维度的分析,从而形成了图3较为清晰的解题方案.

四、实施方案,完善解题过程

在确定解题方案后,课堂上以独立实施方案的方式解答问题,并在各自完成解答的基础上进行小组合作交流,完善解题过程,从而形成两种模型的解题路径,也为后续解法的迁移积累活动经验.

路径1(解几模型):建立如图4所示的直角坐标系.

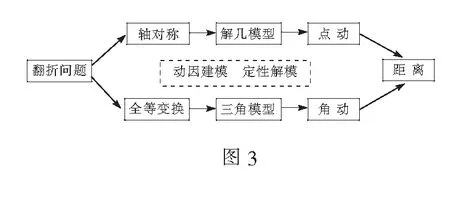
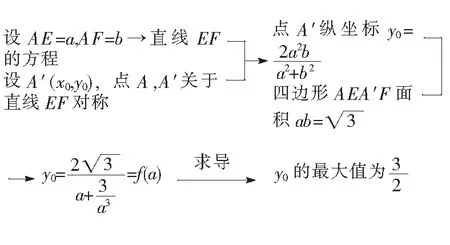
路径2(三角模型):过点A′作AB的垂线A′T,垂足为T,如图5所示.

五、经验迁移,强化巩固认知

例2(改编自2017年江苏高考数学第18题)一位创业青年租用了一块等腰梯形的田地ABCD(如图6)来养蜂、产蜜与售蜜.经测量,AB长为200米,CD长为600米,AB与CD相距200米,田地内有一条笔直的小路EF(E在BC上,F在AD上)与AB平行且相距50米.现拟从入口处A再修一条笔直的小路AN与BC交于N,在小路EF与AN的交点P处设立售蜜点(小路的宽度不计)

(2)两条小路EF与AN将田地划分为四个区域,现将图中阴影部分规划为蜂巢区,空白部分规划为蜂源植物生长区.若要使蜂源植物生长区的面积最大,该如何修建小路AN?

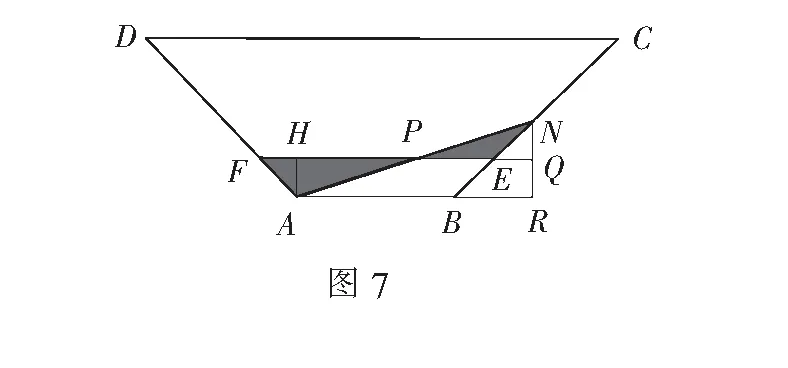
设计意图本例题第(1)问与2017年江苏高考第18题有极高的相似性,本质相同，属于“静态图形求值问题”．就难度而言，第(2)问更为复杂,这是在第(1)问基础上延伸出来的“动态图形最值问题”,与例1中的第(2)问属同类.之所以对高考题做改编，是为了两道例题在教学上的衔接和解法的迁移,更重要的是能进一步帮助学生提炼以几何图形为背景的这类应用题的解题路径．本题的第(2)问实质是已知等腰梯形上、下底边、高以及EF的长度,求何时空白区域面积最大(见图7)?由于空白区域不规则,因而我们可转化为求阴影部分面积最小值的问题．为了引导学生建模,设计如下一组问题:

问题6影响阴影部分图形面积变化的因素有哪些?

问题7追根溯源,什么是导致面积变化的“源头”?

问题8能将“源头”用变量来表示吗?

对于问题6,同学们结合图形不难发现,导致面积变化的因素是FP,PE的长度以及∆PNE的高．而进一步追根溯源,寻求这些因素变化的源头,那么就仁者见仁智者见智了．立足的角度不一样,得到的答案也就不一样．有同学认为源头是“点P的变化”,也有认为源头是“直线AN的变化”．对于问题8,更是呈现出多样性的刻画方法,同一源头也引入了各不相同的变量．对于同样认定源头是“点P的变化”,但选择变量时有以点P的坐标为参数,也有以FP的长度为参数;对于同样认定源头是“直线AN的变化”,在选择变量时有以直线AN的斜率为参数,有以∠BAN为参数,也有以点N的坐标为参数．将上述三个问题剖析清楚,学生也就不难建立对应的数学模型．无论哪种建模方式,都是紧扣了点或线的“变化”,也就是前文所述的“动因”.

问题9要解决这个数学模型,要表示出图形中的那几个关键量?

问题10可以考虑引入哪些参数来表示这些关键量?

问题11表示这些关键量的过程中,图形的哪些几何特征是我们的突破点?

设计意图由于建模类型的多样性,因而“解模”的过程各不相同．对于本题其解模的关键在于教师引导学生用参数表示FP,PE的长度以及∆PNE的高,进而才能解决模型中的阴影面积问题．观察题中几何图形,无论哪类模型,选择哪个变量为参数,都需要依托“AB∥CD∥EF”的几何性质来突破,也就是前文所述的抓“定”性解模．以“三角模型”为例,对解模过程进行简单分析．在三角模型中引入角参∠BAN=θ,需要思考的是如何用θ来表示FP,PE的长度以及∆PNE的高(或NE的长度)．FP的长度应在∆PAF中解决,PE的长度和∆PNE的高(或NE的长度)显然在∆PNE中解决．进一步考虑,如何将θ与∆PAF和∆PNE联系起来?这时依据“AB∥CD∥EF”,发现∠BAN=∠EPN=∠APF=θ,进而就可以分别在∆PAF和∆PNE中利用正余弦定理表示出FP,PE和NE的长度,也就解决了表示阴影面积的问题.