随机利率模型下基于Tsallis熵分布的可转债定价

常竞文， 王永茂

（燕山大学 理学院，河北 秦皇岛066004）

0 引言

可转换债券是由公司发行的债券，持有者在将来某些时刻有权将债券转换为公司的股票。在对可转换债券定价时，信用风险起着非常重要的作用，忽略信用风险会高估券息和本金的价值，计算出的债券价格会不准确。1998年，Tsiveriotis K和Fernandes C［1］在对可转债定价过程中考虑到存在违约风险的情况，此模型的提出使得众多学者意识到在可转债定价过程中信用风险存在的必要性，李念夷和陈懿冰［2］同时将三叉树模型与信用风险考虑到可转换债券定价模型之中，Xiao T［3］研究了当模型依赖于瞬时违约风险的概率分布时可转换债券的定价问题。

由于会受到利率的影响，可转换债券需寻找到一个平衡价格来消除可转债发行者与其持有者的套利机会。潘坚和肖庆宪［4］在具有违约风险的基础上，利用Feynman-Kac表示定理和偏微分方程方法研究随机利率下的可转换债券定价问题。

然而，上述文章在对可转债定价的过程中，仍然存在着问题导致定价结果不够准确。可转债价格与其标的股票价格存在高度相关的关系，而上述文章所研究的可转债定价问题，其标的股票的价格是基于正态分布的，大量实证研究表明，股票市场日收益率分布具有“尖峰肥尾”的特征，因此众多学者开始尝试用新的分布对股票日收益率数据进行拟合，Mandelbrot［5］首次研究稳定Pareto分布，但因其具有无限方差并未被广泛应用于金融期权定价。另外一种常见分布是假设价格模型服从Levy分布一族［6，7］，但其密函函数的复杂性限制了其在金融定价领域中的应用。

巴西物理学家Tsallis［8］提出的Tsallis熵分布可以用来描述具有非线性，长期记忆效应和相互作用的系统。文献［9，10］均对股票市场收益分布进行研究，用Tsallis熵分布替代正态分布，对股票价格过程进行建模，相比于传统的B-S公式，其显著特点就是非广延参数的存在，且不同的值对期权的定价呈现出一定的差异性，研究结果表明Tsallis熵分布可以很好地刻画股票市场日收益率分布的尖峰肥尾的特征。在国内，基于Tsallis熵理论，张磊和苟小菊［11］研究发现股价具有反常扩散特征和非线性动力系统特征。赵攀和肖庆宪［12］研究得到了股价模型基于Tsallis熵下的期权价格的计算公式。焦博雅和王永茂［13］在此基础上将更新过程引入期权定价过程中，并进一步证实于Tsallis熵分布下的股价波动更接近于市场真实的股价波动。

以上文献均是将Tsallis熵理论应用到期权定价过程中，但基于Tsallis熵分布的可转换债券定价有待进一步研究。本文在研究可转债的定价过程中，一方面考虑到了随机利率及存在瞬时违约风险的问题，另一方面用Tsallis熵分布替代正态分布，对标的股票价格过程建模，利用有限元法得到可转债价格满足的偏微分方程的数值解，根据市场真实的股票及可转债数据进行实证分析，期望理论定价结果与市场真实可转债价格更加吻合。

1 双因子建模：随机利率下的可转债

1.1 股票价格模型

可转债价值在连续无摩擦市场的表达形式形式为V＝V（S，r，t），其中S为股票价格，利率r为一个自变量。假设t时刻股票价格S（t）满足下述随机微分方程：

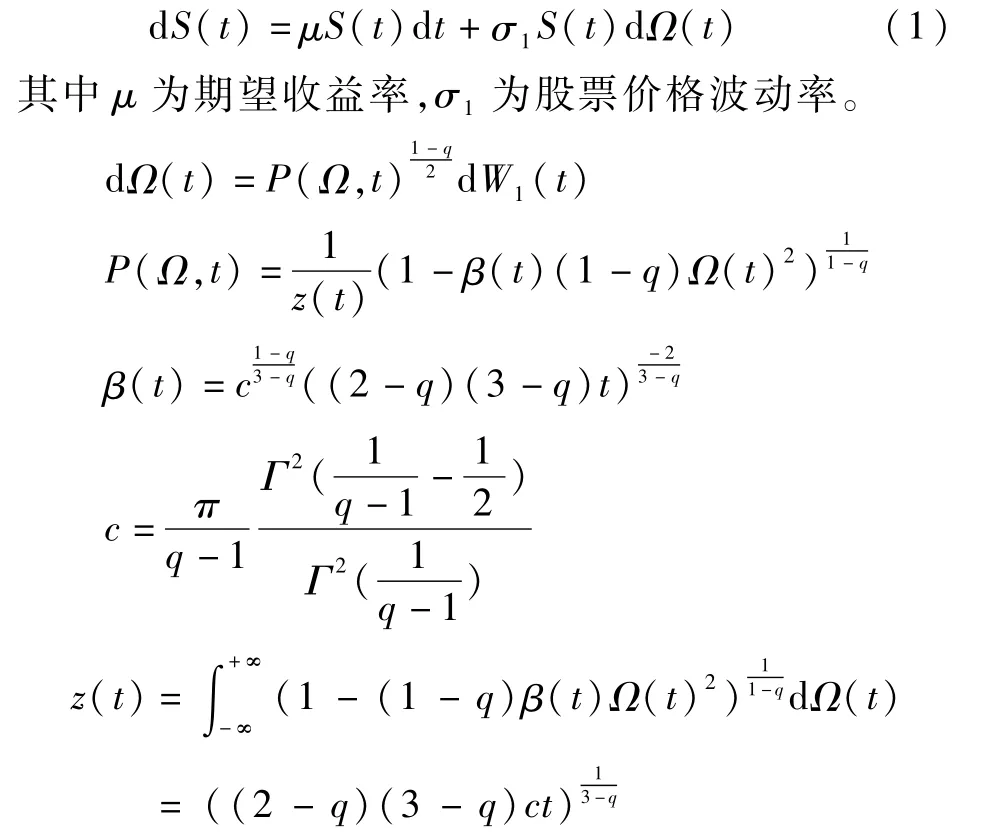
Γ（·）为Gamma函数；Ω（·）表示服从非广延Tsallis熵分布的随机变量，E（Ω（t））＝0，D（Ω，t）＝（（5-3q）β（t））-1，1＜，P（Ω，t）来源于物理学中的Tsallis熵理论，当q＝1时，P（Ω，t）退化为均值为零的正态分布。

｛W1（t）：0≤t≤T｝是标准维纳过程。

1.2 随机利率模型

在风险中性市场，假定利率r（t）服从Vasicek模型，即满足随机微分方程：

其中：θ为常数，表示长期均衡的利率水平；u为平均回复率；σ2为利率的波动率；｛W2（t）：0≤t≤T｝是标准维纳过程，W1（t）与W2（t）的线性相关系数为ρ，其中：-1≤ρ≤1。

1.3 可转债的可赎回和可回售特性

可转债常常带有可赎回特性，给予了发行公司在任意时候或特定时间段用约定的金额将债券购回的权利，此金额随时间变化，将其记为MC，如果公司可以以MC将债券赎回，则根据无套利条件可以得到V（s，r，t）≤MC；有些可转债附带可回售特性，即允许债券持有人以一定金额MP将债券卖给发行公司，施以约束V（s，r，t）≥MP，对持有人而言该特性增加了债券的价值。

2 泊松过程与瞬时违约风险

2.1 瞬时违约风险

如果在t时刻公司还未曾发生违约，而瞬时违约风险为p，那么在时刻t和t+dt之间公司的违约概率为pdt。在无任何事情发生的情况下突然出现一个状态变化，这符合泊松过程的变化规律。

假设为p一个常数，令P（t，T）表示公司在到t时刻为止还未曾发生违约的条件下，在T时刻也不会违约的概率。公司在稍后的t′时刻t′+dt和时刻之间发生违约的概率等于pdt乘以公司到t′为止都没有发生违约的概率，即P（t′+dt，T）-P（t′，T）＝pdtP（t′，T），将上式展开，用于考察极小时间步长的结果，可以得到一个常微分方程。该方程代表了所求概率的变化率∂P／∂t′＝pP（t′，T），若公司一开始没有处于违约状态，那么P（T；T）＝1，该微分方程的解为e-p（T-t）。因此，在T时刻支付1美元的零息票债券的价值可以用期望现金流的现值来建模，其结果为e-p（T-t）Z，Z是与风险债券的到期期限相同的无风险零息债券的价值。该债券到期收益 率 由 下 式 给 出即信用风险以利差p影响收益率的大小。

2.2 可转债价格满足的偏微分方程

考虑可转债价格V（s，r，t），且V（s，r，t）关于t连续可微，关于s和r二次连续可微，根据广义It＾o公式，可以得到

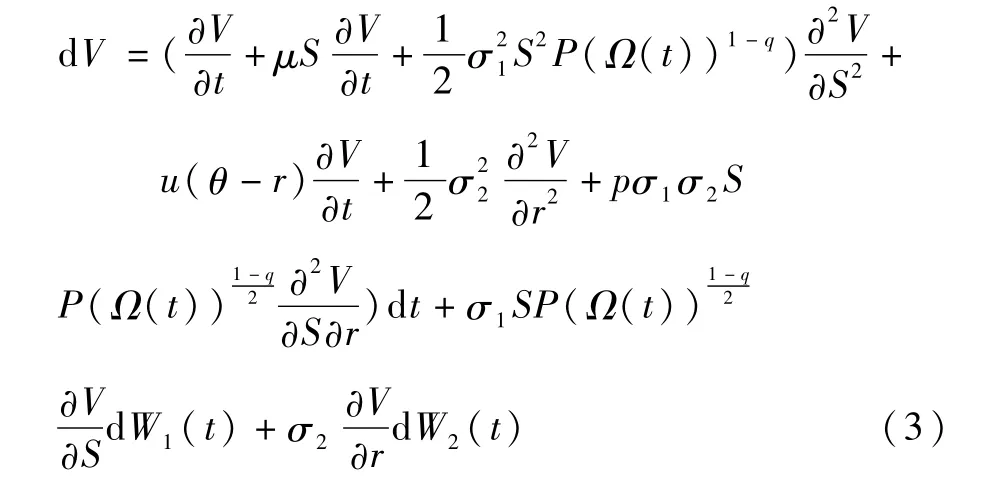
现考虑在定价过程中加入违约风险。在瞬时随机利率与泊松过程的扩散变化不相关的前提下，构建对冲组合：买入一份到期日为T1的可转债V1，卖出Δ2份到期日为T2的可转债V2和Δ1份股票s，即

若公司当前未发生违约，那么在接下来的（t，t+dt）时间段中，存在两种情况。一种情况是有（1-pdt）的概率可转债不违约，在这种情况下，组合价值在单位时间步长下发生的变化为

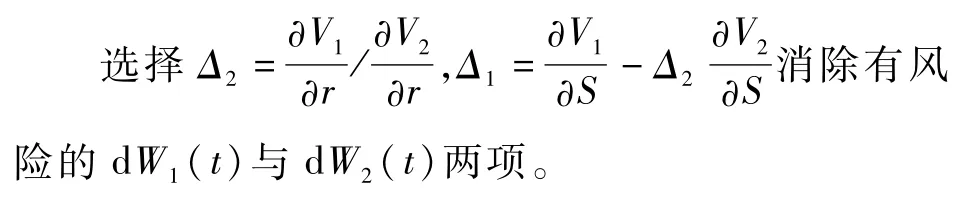
另一是可转债违约的概率是pdt，违约风险发生导致突然损失，组合价值变化为：

这里解释一下η*与R*的含义。

η*表示信用风险折现因子，η*＝η+Xg，g为风险补偿，且0≤η*≤1，在违约时刻来临时，s+＝s（1-η*），s+表示违约事件发生后股票的瞬时价格，s表示违约事件发生前股票的瞬时价格。当η*＝0时，代表在瞬间违约事件发生时股价未产生变动；当η*＝1时，代表公司发生严重违约事件，股价在违约事件发生后瞬间为零。X服从0-1分布，X＝0代表可转债价格处于实值，X＝1代表处于虚值。

η*的意义在于当违约事件发生时，股价在原价格基础上下落一个百分比，更加接近违约事件发生时的公司真实情况。

R*补偿因子，0≤R*≤1，处理方法同η*。

公司违约事件发生时，债券持有人若选择将可转债转换为股票，此时可转债的价值变为：ns（1-η*），n为转换比率；若选择继续持有可转债，则其价值变为：R*F，F为可转债面值。

针对上述两种组合价值变动，取期望并省略dt高阶项，进而由无套利原理，得到

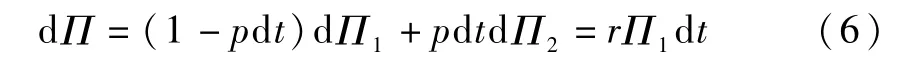
将（4）和（5）代入（6）式，有

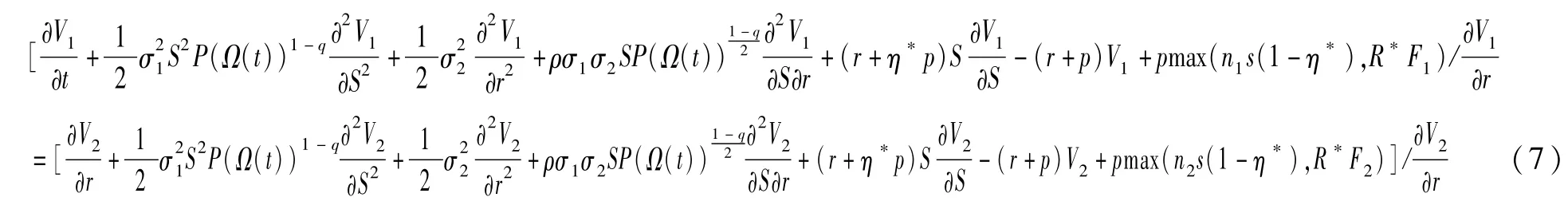
（7）式两端形式相同，说明两端方程式等值且此值与可转债性质无关，假设此值为m（r，s，t），即

假设风险市场价格为零，则根据文献［14］，

一项由公司的违约情况决定，主要与股票价格相关，若股票风险价格为λ1（s），则：

上式即为基于Tsallis熵的具有随机利率及违约风险的可转债价格满足的偏微分方程。

若利率为常数，忽略存在违约风险情况，（11）式与文献［10］中的（10）式保持一致，即

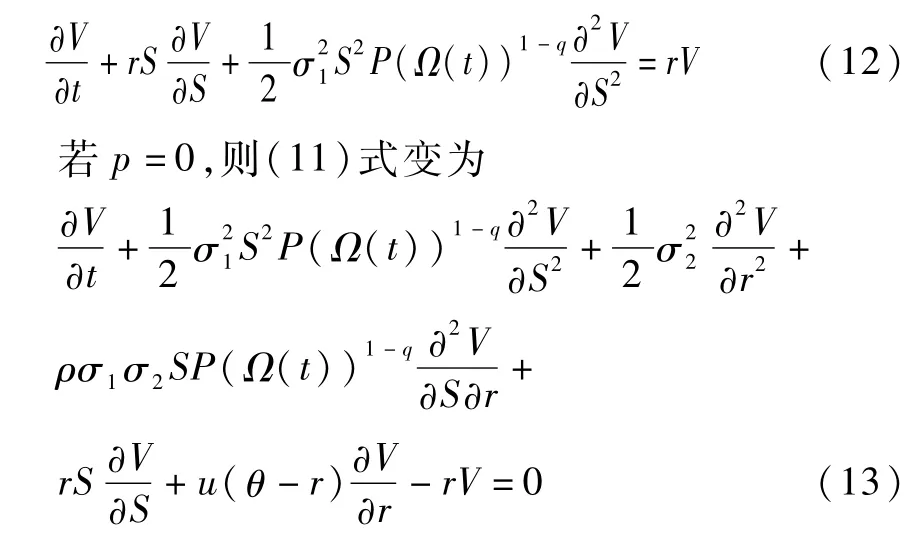
即为基于Tsallis熵的双因素可转债模型。

若q＝1，则（11）式变为

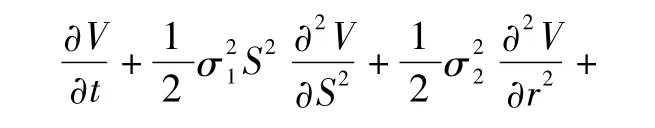
即为具有信用风险的双因素可转债模型。

2.3 自由边界条件

（1）可转债处于转换期内的转换条件：

即其价值大于等于其转换价值；其中n为转换比率。

（2）可转债在赎回期内，其价值的最大值为转换价值和赎回价两者中的较大者，即

（3）可转债在回售期内，其价值的最小值为转换价值和回售价两者中的较大者，即

2.4 终值及跳跃条件

（1）可转债合约到期时，其价值应为可转债的面值与可转债的转换价值两者中的较大者，即到期条件：

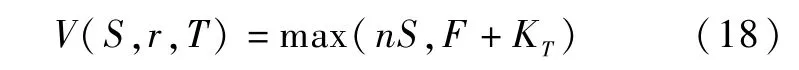
其中：F为可转换债券的面值，KT代表合约到期时可转换债券的息票值。

（2）公司股票价格足够高时，投资者会考虑将持有的可转债转换为股票，因此可转债在此刻的价值是其转换价值，即：

其中n为转换比率。

（3）公司股票价格非常低时，忽略存在回售的情况，可将可转债价值看作普通债券价值，即：

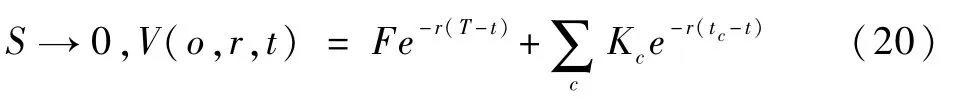
（4）投资者在市场利率足够大的情况下会考虑抛出可转债。忽略存在赎回和回售两种情况，可转债价值为零，即：

（5）可转债价值在市场利率非常低甚至趋于零时的情况下不易确定。可认为可转债价值对于利率的偏导有限，即：

（6）假设息票每半年支付一次，所以有每个息票日的跳跃条件，即：

其中Kc为第c次所付利息，tc为第c次付息时间。

3 有限元法

3.1 自由边界处理

由于可转债具有可赎回、可回售和转换特性，可对其自由边界处理为线性互补问题，在此定义微分算子：

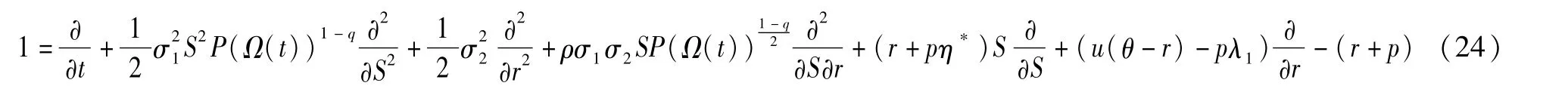
若Mc＜ns，则债券持有者会选择转股，可转债的价值变为：

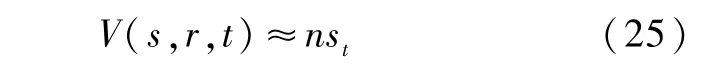
若Mc≥ns，则将其自由边界处理为以下线性互补问题：

其中：D＝pmax（ns（1-η*），R*F）。

此问题可用基本迭代方法求解。

3.2 有限元法计算格式

可转换债券定价采用有限元法，相比于有限差分，有限元法精度更高，它是对整个区域进行求解的，而有限差分法仅仅是计算孤立点的价格，另外有限元法对边界及终值条件处理效果更好。

有限元方法把未知函数V（s，r，t）中的空间变量（s，r）与时间变量t分开处理，本文先利用半离散方法对空间变量（s，r）离散，然后利用全离散方法对时间变量t离散。

步骤1利用变分原理及格林公式得到积分方程。

设求解区域为Ω＝［Smin，Smax］×［rmin，rmax］，则根据变分原理［15］，（11）式变为以下积分方程：

其中，H1（Ω），（Ω）称为Sobolev空间，两者的形式分别为：H1（Ω）＝｛f（S，r）｜fα（S，r）∈L2（Ω），α＝0，1，…，k｝（Ω）＝｛f（S，r）｜f（S，r）∈H1（Ω）且f｜Γ0＝0｝，其中，fα（S，r）表示具有直到k阶广义导数f（S，r）的全体。Γ0对应（20）、（21）所表示的边界条件，在这里，当利率趋于零时，（20）式可以表示为［14］：

在微分方程（27）中存在二阶导数积分，处理此积分需利用到数学微积分中的格林公式：

其中：Γ表示（28）式所对应的边界条件。

对方程（27）应用格林公式并代入（28）式有：

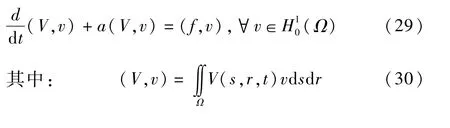
步骤2构造单元局部坐标系，建立插值函数。

将求解区域Ω分成N×N个矩形，节点坐标｛（Si，ri），i＝1，2，…，N｝，任意一个矩形单元ek的四个顶点对应的节点编号为（k1，k2，k3，k4）。其中单元的形心被视作为坐标原点：ek＝｛（S，r）｜Sk1≤S≤Sk2，rk1≤r≤rk4｝，k＝1，2，…，N×N，因此，方程（29）可以表示为

其中（V，v）ek，a（V，v）ek以及（f，v）ck定义类似于（30）、（31）和（32）式，仅是将积分区域Ω换成ek

我们将单元归一化，即采用无量纲坐标（ξ，η），通过仿射变换：

得到标准单元：ek＝｛（ξ，η）｜-1≤ξ≤1，-1≤η≤1｝，其中k1，k2，k3，k4四个节点的坐标分别为（-1，-1），（1，-1），（1，1），（-1，1）。

在每一标准单元上，定义矩形单元上ek上的Lagrange双线性插值函数：

其中Ni（ξ，η）为矩形单元的形函数矩阵：

Vki（t），vki分别对应于矩形单元ek的四个顶点的函数值和扰动值。

步骤3矩阵及总刚度矩阵的形成。

将（34）代入式（33）中，根据变分预备定理［15］

可知vk的任意性，则式（33）可写为：

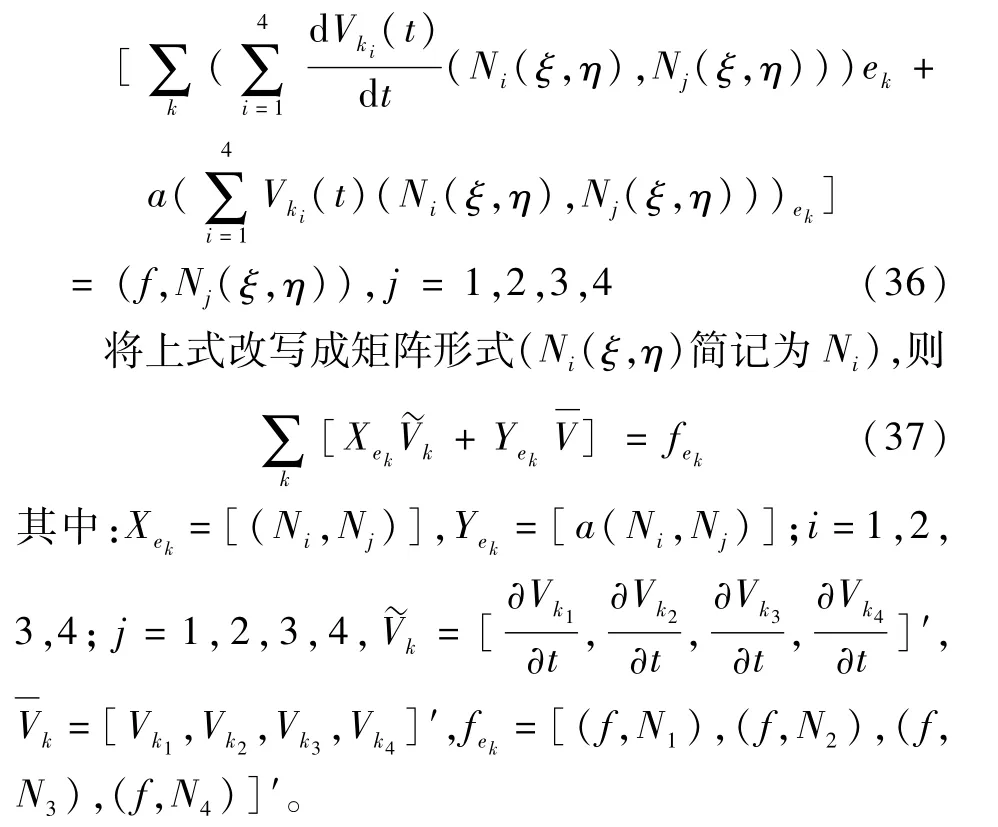
接下来，我们利用单元节点编号与整体编号的关系，把单元刚度矩阵进行叠加，形成总刚度矩阵，方程（37）可改写为：

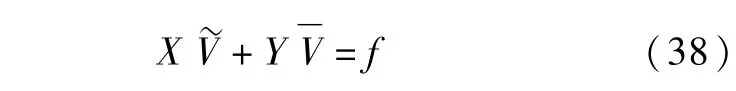
步骤4时间变量的离散化处理及可转债价格的推导。

取正整数K，并令tk＝kτ，0≤k≤K，其 中τ＝T／K。对（38）式建立如下格式

取θ＝1／2，（39）式为Crank-Nicolson全离散格式，根据（39）式可得到迭代方程：

首先根据终值条件（18）可得到到期日可转债的价格，进而采用基本迭代方法，利用方程（40），对时间变量进行回溯，结合约束条件（16）、（17）可得每个节点时刻可转债价格，最终通过插值函数（34）便可得到每一时刻对应不同股票价格和利率的可转换债券的价格。

4 实证研究

4.1 基于Tsallis熵分布的股票价格模型

选取在2018年3月份上市、期限为6年的长证转债、利欧转债、敖东转债的对应标的股票——长江证券、利欧股份、吉林敖东进行实证分析，将每日收盘价作为样本数据（选取日期：2016年1月4日～2018年9月28日；数据来源：RESSET数据库）。样本容量分别为671、656、665。日收益率利用ri＝（si-si-1）／si×100%计算，研究对象为标准化日收益率。计算软件Rstudio。收益率时间序列见图1～图3，三种证券日收益率基本统计量见表1。

图1 长江证券日收益率序列图

图1、2、3显示三种股票日收益率的波动具有显著的集聚性，说明股票价格很容易受到外来因素影响，进而产生连续的跳跃波动，并且股票价格的时间序列在一定程度上表现出较强的记忆性。

由表1峰度值和偏度值可知，三种标的股票日收益率具有明显的“尖峰肥尾”特征，且K-S检验的p值小于0.05，可知日收益率分布在95%置信度下拒绝接受服从正态分布假设。另外，图4～图6显示出日收益率具有“左偏尾”和明显的“尖峰肥尾”特征，且与正态分布曲线吻合度低，以上阐述表明传统的基于几何布朗运动的股票价格波动与真实股价波动存在较大差异，可尝试利用其它分布来模拟真实的数据分布。

图2 利欧股份日收益率序列图

图3 吉林敖东股票日收益率序列图

表1 股票日收益率的基本统计量

接下来用Tsallis熵分布对日收益率进行拟合，采用最优拟合实际日收益率分布的方法来估计最优参数q。首先，标准化实际日收益率并将其作为实际分布；其次，利用蒙特卡洛方法进行数值模拟，得到各q值下的模拟收益率序列并将其作为理论分布；最后，对q∈（1，5／3）进行穷举，计算出各确定q值下日收益率理论分布与实际分布的最优拟合优度值，其对应的q值即为需要Tsallis熵分布的最优参数。

依据以上所阐述的步骤估计出的Tsallis熵分布的针对三种股票的最优参数值分别为q＝1.42，1＝1.44，q＝1.51。将其模拟得到的日收益率理论曲线与日收益率实际曲线进行比较，结果见图4、5、6。

图4、5、6显示Tsallis熵分布的优势在于在峰度以及尾部特征上对日收益率的拟合更好，且对应三种股票的最优参数值分别为q＝1.42，q＝1.44，1＝1.51。基于此，在之后对可转债定价研究过程中将其标的股票价格模型服从正态分布进一步修正为服从最优参数q值下的Tsallis熵分布。

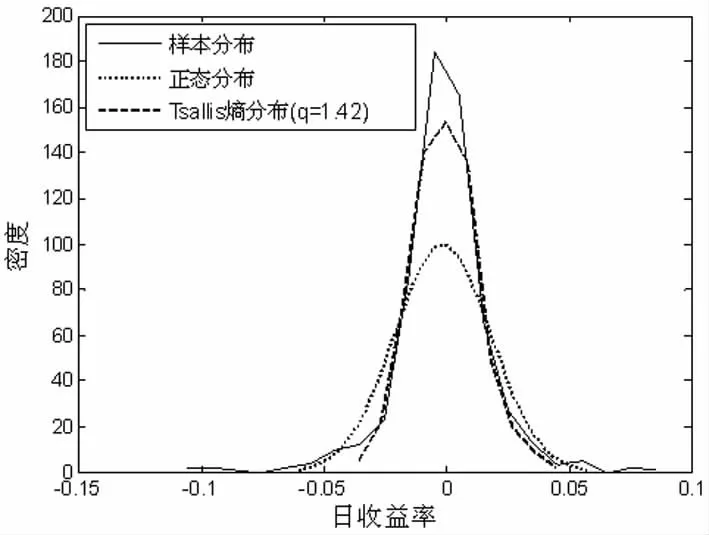
图4 长江证券日收益率分布和正态分布及Tsallis熵分布曲线比较

图5 利欧股份日收益率分布和正态分布及Tsallis熵分布曲线比较

图6 吉林敖东日收益率分布和正态分布及Tsallis熵分布曲线比较

4.2 可转债价格的实证分析

本文实证分析中，选取对象为长证转债、利欧转债、敖东转债，三者上市日期接近且期限均为6年。

长证转债（127005）基本要素：期限：6年（2018年3月12日～2024年3月12日）：债券面值：100元；票面利率：第一年0.2%，第二年0.4%，第三年1.0%，第四年1.5%，第五年1.8%，第六年2.0%；发行张数：5000万张；实际发行规模：5000百万元；转股起止日期：2018年9月17日～2024年3月11日；转债评级：AAA。

利欧转债（128038）基本要素：期限：6年（2018年3月22日～2024年3月12日）：债券面值：100元；票面利率：第一年0.3%，第二年0.5%，第三年1.0%，第四年1.5%，第五年1.8%，第六年2.0%；发行张数：2197.5万张；实际发行规模：2197.5百万元；转股起止日期：2018年9月28日～2024年3月21日；转债评级：AA。

敖东转债（127006）基本要素：期限：6年（2018年3月22日～2024年3月12日）；债券面值：100元；票面利率：第一年0.2%，第二年0.4%，第三年0.6%，第四年0.8%，第五年1.6%，第六年2.0%；发行张数：2413万张；实际发行规模：2413百万元；转股起止日期：2018年9月19日～2024年3月12日；转债评级：AA+。

本节主要研究加入Tsallis熵后可转债价格变化情况，研究对象为三种可转债从刚上市到转股期开始这个时间段的价格变化。在利率为常数的前提下可转债价格满足偏微分方程（12）式。

长江证券的波动率估计：采用GARCH（1，1）模型计算波动率得到：

对应于α＝0.0470022，β＝0.9272747，ω＝γVL＝6.400797×10-6。由α+β＜1可知模型通过平稳性检验，且根据α+β+γ＝1可计算得到隐含长期每日方差平均为：VL＝2.488×10-4。长江证券每年均有244个交易日，则年波动率

同理可得到利欧股份股票波动率σ2≈0.25，吉林敖东股票波动率σ3≈0.237。

取到期日与长证转债相近的七年期国债（019216）的票面利率作为无风险利率，即r≈0.0325。

转换比率（可转债面值／转股价）分别为：n1＝13.157，n2＝36.232，n3＝4.735。

利用单因子有限元方法绘制三维图并计算得到长证转债、利欧转债及敖东转债的理论价格。所用软件：Matlab。选取三种可转债交易天数均为107天，其中长证转债（2018年4月11日～2018年9月10日）、利欧转债（2018年4月19日～2018年9月19日）、敖东转债（2018年5月11日～2018年10月17日）。基于Tsallis熵分布的三种可转债理论价格及其与实际交易价格对比图如图7～图12所示。

图中理论价格1与2分别表示股价基于正态分布与Tsallis熵分布下可转债价格。

图7 标的股价基于Tsallis熵的长证转债价格三维图

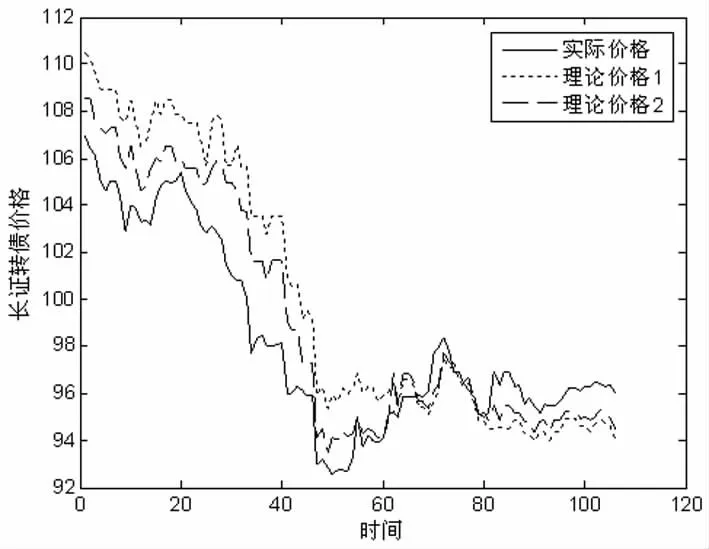
图8 长证转债的实际价格与理论价格对比图

图9 标的股价基于Tsallis熵的利欧转债价格三维图

图10 利欧转债的实际价格与理论价格对比图

图11 标的股价基于Tsallis熵的敖东转债价格三维图

图12 敖东转债的实际价格与理论价格对比图

图7、图9、图11所示分别为长证、利欧、敖东转债价格与时间（6年期限）、相对应标的股票价格的三维图。

图8、图10、图12所示分别为长证、利欧、敖东转债从刚上市到邻近转股期时间段。图中显示：相比于理论价格1，股价基于Tsallis熵分布的可转债理论价格2更加贴近于市场实际价格。

以上分析说明基于T sallis熵分布的理论定价结果更贴近于可转债真实的价格波动。

5 结论

（1）本文主要研究了在随机利率下股价基于Tsallis熵分布及带有瞬时违约风险的可转换债券定价问题，并利用有限元法得到了可转债价格所满足的偏微分方程的数值解。

（2）对三支市场可转债进行实证研究。根据可转债标的股票的市场真实数据模拟收益率序列，发现股价模型基于Tsallis熵分布下曲线拟合明显优于传统的正态分布，并得到了Tsallis熵分布的最优参数。在此基础上，绘制可转债理论价格的三维图和理论价格与实际价格对比图。研究结果发现，在可转债刚上市至临近转股期的时间段内，股票价格基于Tsallis熵分布情况下的理论价格更加贴近于市场实际价格。因三支可转债为6年期可转债，故对其更准确的定价有待进一步的研究。