考虑繁忙率的多时段救护车优化布局研究

李 瑞， 苏 强， 祝延宏， 王 谦

（1.同济大学 经济与管理学院，上海200092；2.上海市第一人民医院，上海200080；3.中国人民解放军第二军医大学 第三附属医院，上海200433）

0 引言

院前急救是现代急诊医疗体系中重要的一环，它包含从突发事件起病人拨打急救电话，120指挥中心委派救护车辆，相应医护人员抵达现场进行救治，以及必要时将病人转运至医院急诊室进行进一步抢救的整个过程。它与院内急诊科、重症监护室等相关医疗科室共同组成急诊医疗服务体系，是城市应急保障体系的重要组成部分。时间性、多样性、不可预见性是院前急救的鲜明特点，救护车作为院前急救中不可或缺的重要角色，更是承担着对时间分秒必争的重任。

据相关文献［1］报道，重症急救患者中，仅不到10%的人是由于原发疾病致死，更多的是由于等待救援时间过长引发更为严重的并发症，最终导致死亡。合理的救护车布局方案可以保证在有效时间内响应更多的急救需求，达到一定的服务水平，有助于建设高效、完善的院前急救服务体系。

对救护车布局问题的研究最早可以追溯到上世纪70年代，在早期的研究中，最经典的两个模型分别是Toregas［2］提出的LSCP（Location Set Covering Problem）模型和由Church与Revelle［3］提出的MCLP（Maximal Covering Location Problem）模型。其中LSCP模型考虑在覆盖所有需求点的情况下最小化所需救护车数量，MCLP模型则考虑在救护车数恒定的情况下最大化覆盖需求量。但这两个经典模型均只考虑了需求点被一次覆盖的情况，这导致如果一辆救护车覆盖的区域同时发生两次急救需求，必须放弃一个急救需求，这显然不符合实际。为了提高系统救援能力，Daskin和Stern［4］在MCLP模型的基础上提出最大化二次覆盖需求量。之后，Gendreau等学者［5］提出了双标准覆盖模型DSM（Double Standard Model），首次引入两个覆盖圈半径，在保证所有需求都能被大圈覆盖的情况下，最大化被小圈两次覆盖的需求数。本文即是在双标准覆盖模型的基础上考虑了救护车的繁忙率，并探究一天内不同时段的繁忙率带来的不同布局方案。繁忙率最早是由Daskin［6］在MEXCLP（Maximum Expected Covering Location Problem）模型中提出的，之后的学者Rapede和Bernardo［7］建立了不同时段需求不确定型模型，简称TIMEXCLP模型。Jagtenberg等人［8］提出了动态MEXCLP模型解决实时动态布局问题，系统中每出现一次急救需求，都要重新进行一次决策。

从既有文献可知，在救护车布局领域，大部分研究主要来自国外学者，国内的研究相对较少。宋元涛，杨文国和黄钧［9］提出有数量限制的双覆盖标准救护车选址模型，并利用禁忌搜索方法对模型进行求解。苏强等人［10］对双覆盖模型进行改进，提出以最小化延误成本和运营成本为目标函数。不同学者从不同角度对问题进行剖析。

本文的主要贡献在于在传统的双覆盖模型基础上考虑到当急救需求产生时，救护车有的一定的概率处于繁忙状态，此时无法立即响应需求，故在模型中引入繁忙率。此外，由于每天不同时段下需求产生频率的不同，救护车的繁忙率也随时段而改变，故本文提出多时段下的救护车布局方案。

1 问题描述

1.1 基本概况

在本研究中，假设共有p辆救护车，n个需求点，需求点集合V＝｛v1，v2，…，vn｝，其中任意需求点vi处的需求为λi；有m个备选站点，备选站点集合W＝｛w1，w2，…，wm｝，其中任意备选站点wj处停放的救护车数记为yj。结合实际情况，每个救护车备选站点都有其相应的承载上限，故这里规定备选站点wj处的救护车承载上限为pj。救护车从备选站点wj到需求点vi的行驶时间为tij。在双标准覆盖模型中，标准一为保证所有需求都能够在一定的时间内被响应。由于覆盖的全面性，这个时间通常比较久。标准二为保证至少有α比例的需求能在较短时间内被响应。这两个规定时间记作r1和r2（r1＜r2）。定义三个0-1变量γij，δij和。当行驶时间tij≤r1时，规定γij＝1，否则γij＝0；当行驶时间tij≤r2时，规定δij＝1，否则δij＝0。＝1表示需求点vi被覆盖了k次，这里k＝1，2，…，p。现实中，一辆救护车并不可能是24小时待命状态，当急救电话打进时，救护车可能正在奔赴上一个需求点的途中，也可能在其他需求点等候医护人员对病人进行检查或抢救，也可能在将病人转移到医院急诊室的途中等等，这些情况下救护车都无法立即响应新的需求，即处于繁忙状态。因此，在解决问题时，应该考虑每辆救护车在不同时段下的繁忙率，这也是本文的主要创新点所在。

1.2 考虑繁忙率的期望覆盖需求的计算

我们可以通过向专家及相关人员咨询的方式获得救护车的繁忙率q的值。本文假设所有的救护车繁忙率相同，且任意两辆救护车之间的状态不存在相关性，即一辆救护车是否可用的概率与另一辆救护车是否可用是独立的。在上述设定下，可计算出任意时刻系统中有t辆待命救护车的概率为：

同时我们也可以计算出需求点vi被k辆救护车覆盖，且k中至少2辆处于待命状态的概率为：

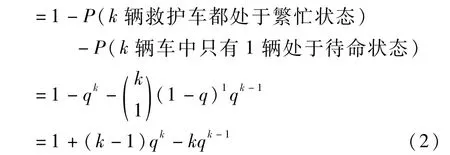
P（需求点vi被k辆救护车覆盖，且k中至少2辆处于待命状态）故可以得到被k辆救护车覆盖，且k中至少2辆处于待命状态的需求点vi处的需求期望值：

从k辆车减少到（k-1）辆车产生的需求期望差值为：

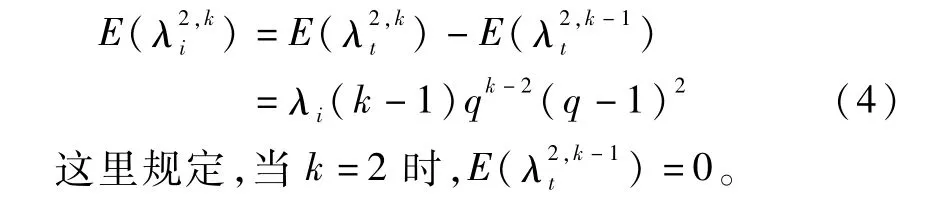
1.3 多时段的划分

为了更接近实际情况，可以将繁忙率进一步按照时间、空间标准进行细分。本文考虑到不同时段需求产生率的不同，将一天按照早、晚高峰时段共划分为5个时段h1-h5，其中h1表示“早间时段”，h2表示“早高峰时段”，h3表示“白天非高峰时段”，h4表示“晚高峰时段”，h5表示“晚间时段”。不同时段救护车具有不同的繁忙率qh（h＝1，2，…，5）。表1列举出多时段划分法的基本框架。

表1 多时段的划分及其繁忙率表

2 考虑繁忙率的多时段布局模型的构建

模型涉及到的相关变量已经在问题描述部分加以阐明，为了简化分析，假设需求点位置及需求是确定的，且需求产生服从均匀分布。为解决院前急救中的救护车布局问题，本文提出以最大化全天在r1时间内被覆盖至少2次的期望总需求量为目标函数的优化模型。构建的模型如下：

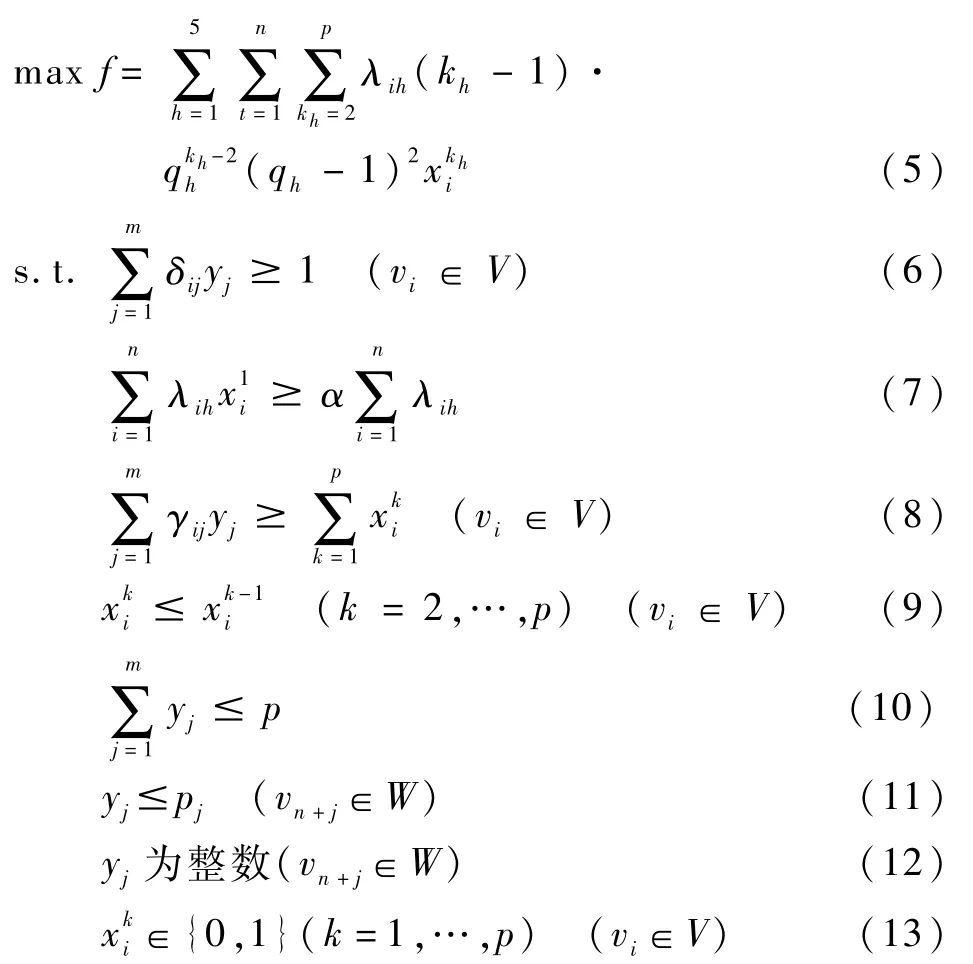
在上述模型中，（5）式为目标函数，表示在考虑救护车在不同时段繁忙率的情况下，全天能够在r1时间内被至少2辆救护车响应的需求的期望最大值，其中λih表示在th-th+1时段内，任意需求点vi处的需求。（6）～（13）式为约束条件。（6）式为单覆盖要求，保证每个需求点vi都能被救护车在r2时间内响应，即双标准覆盖模型中的标准一。（7）式表示能被救护车在r1时间内响应的需求数占总需求数的比例大于α，即双标准覆盖模型中的标准二。（8）式约束了目标函数中的时间限制为r1，同时它保证了当＝1时，能在r1时间内响应vi处需求的救护车数量至少为1；当＝1时，能在r1时间内响应vi处需求的救护车数量至少为2。约束（9）确保了当需求点vi没有被覆盖（k-1）次时，其不可能被覆盖k次。（10）式表明布局的救护车总数不超过现有救护车数。（11）式约束了每个备选站点安置的救护车数不超过该站点可安置救护车数的上限。（12）式为整数约束。（13）式表示需求点vi是否被覆盖k次为0-1变量。

3 算例比较实验

为了验证模型的有效性与改进性，将模型与传统的双覆盖模型进行比较。为使随机算例具备较强的实际意义，本文的算例规模与上海市松江区院前急救系统的实际规模相当，即24×24平方公里大小的区域被抽象成144个需求点，系统中有8个急救站点，每辆救护车的日繁忙率为0.1，双覆盖模型中两个时间标准分别为r1＝8分钟，r2＝15.6分钟，需求比例α＝0.95。

不失一般性，本文随机生成3个144×8的坐标网络，4种大小的急救需求规模，因此共有3×4＝12组实验来比较两个模型的优劣。

根据上海市松江区院前急救的历史数据，每年的急救需求量大约为总人口的1.5%。考虑到上海市高人口密度的特点，4种急救需求规模的需求人口比例分别为0.5%，1%，1.5%和2%。利用ILOG CPLEX 12.0求解模型，得到的对比结果见表2。

表2 传统双覆盖模型与本文模型计算结果对比

表2中列出了通过传统双覆盖模型与本文模型计算得到的需求覆盖率及相应的运算时间，可以看出，在不同的随机网络下，利用本文提出的模型得到的需求覆盖率均高于传统双覆盖模型的结果，证明了本模型的有效性及改进性。运算时间几乎与需求的规模大小呈正相关关系，但本文提出的模型由于引入了繁忙率这一因素，在运算时间上较传统双覆盖模型略长，在之后的研究中可以通过设计合理的算法来缩短运算时间。

4 实例分析

本文以上海市松江区2014年120急救中心数据为例进行分析。松江区位于上海西南部，近年来经济发展迅速，大量企业入驻，外来人口增加，急救需求也随之增加。松江区人口总量为1，755，900，覆盖面积达24×25平方公里。通过对2014年急救中心数据的预处理，得到该年共发生25，841起急救事故。为了便于之后的计算，现将松江区划分为12×12个正方形，统计每个正方形内的需求量并将其集中于小正方形的某一点，这里选取每个小正方形的中心作为需求点，该点的需求量即为该小正方形的需求量。急救系统中共有8个备选站点，27辆救护车，假定这些救护车为相同型号并具有相同的繁忙率，每个备选站点停放救护车不得超过4辆。每个备选站点的位置可由图1形象化表示。图中A点为中心总站，B点为九亭分站，C点为佘山分站，D点为叶榭分站，E点为新浜分站，F点为泗泾分站，G点为老城区分站，H点为车墩分站。

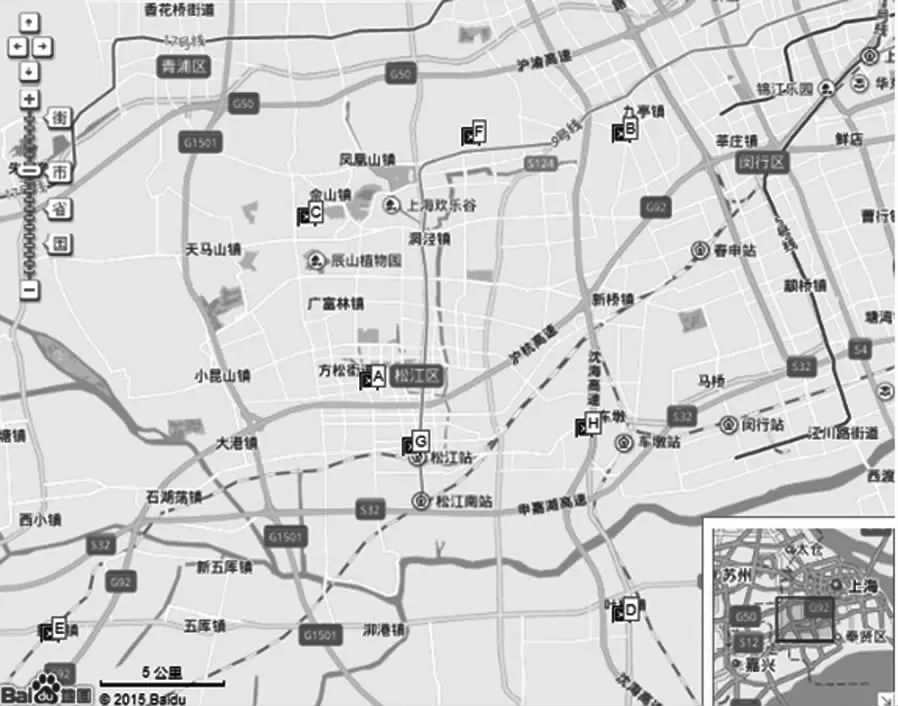
图1 松江区备选站点位置图

救护车的平均行驶速度由历史数据得知为每小时50公里，行驶距离通过起始点的经纬度进行计算，计算公式如下：

Lat1表示地点1的纬度，Lon1表示地点1的经度，地点2同理。

在上海市市委、市政府的重视下，近年来上海急救系统得到了较快的发展，以松江区为例，2005年松江区救护车响应急救需求的时间为20分钟，2010年为15～18分钟，到2014年已达到12～18分钟。基于此情况，本文设定双覆盖模型中两个时间标准分别为r1＝8分钟，r2＝15.6分钟，需求比例α＝0.95。

通过向专家及相关人员的咨询，结合掌握的历史数据，现设每辆救护车的日繁忙率为0.1，利用ILOG CPLEX 12.0求解模型，得到新的救护车布局方案。表3列举了松江区救护车原始布局方案、传统双覆盖模型求解方案与本文模型求解方案的结果对比。

表3 三种救护车布局方案

经计算，在救护车日繁忙率为0.1的情况下，应用本文提出的布局方案比应用原始方案得到的期望覆盖需求量提高了3.19%，比传统双覆盖模型的解得到的期望覆盖需求量提高了0.54%，这充分证明了模型引入繁忙率后的有效性与改进性。从结果中也可以看出，A站点（即中心总站）由原来8辆车减少至2辆车，表明虽然站点处于松江区中心地段，但通过科学计算得到该处并不需要安置过多的救护车，原布局方案下极易产生偏远地区救护车数量不足，对产生的需求应接不暇，而中心总站处救护车闲置的现象，这无疑是一种对资源的浪费。

为了进一步探究繁忙率对救护车布局的影响，令q分别为0.05，0.15，0.25，0.35，得到相应4种布局方案，结果见表4。

表4 不同繁忙率下的布局方案

根据表4可知，当繁忙率从0.05变为0.15时，需从A站点调离1辆救护车到D站点。繁忙率为0.15与0.25时的救护车布局方案相同，无需调动救护车。当繁忙率从0.25变为0.35时，需从D站点调离1辆救护车至G站点。

为了更接近实际情况，考虑将一天划分为“早间时段”、“早高峰时段”、“白天非高峰时段”、“晚高峰时段”、“晚间时段”5个时段，不同时段救护车繁忙率及救护车平均行驶速度由历史数据统计处理后获得。表5列举了5个时段详细的时间划分及该时段下系统的繁忙率及救护车的平均行驶速度。

表5 一天不同时段的划分及其繁忙率、行驶速度表

因此，根据上述结论，可以得到一天5个不同时段下的救护车布局方案，详见表6。

表6 一天不同时段下救护车布局方案

可以看出“早间时段”与“晚间时段”的布局方案相同，其余三个时段布局方案相同。调度仅发生在中心总站（即A站点）与叶榭分站（即D站点）之间。当时间由“早间时段”变为“早高峰时段”时，应从中心总站派1辆车至叶榭分站；而当时间由“晚高峰时段”变为“晚间时段”时，应从叶榭分站调1辆车到中心总站。为了更直观地表现繁忙率q对需求覆盖率的影响，选择这两种不同的布局方案（即表6中的“早间时段”方案与“早高峰时段”方案），探究在应用这两种方案的情况下，需求覆盖率随q的变化。利用Matlab计算出结果，绘制出图2，q根据实际情况，定义为从0到0.4。

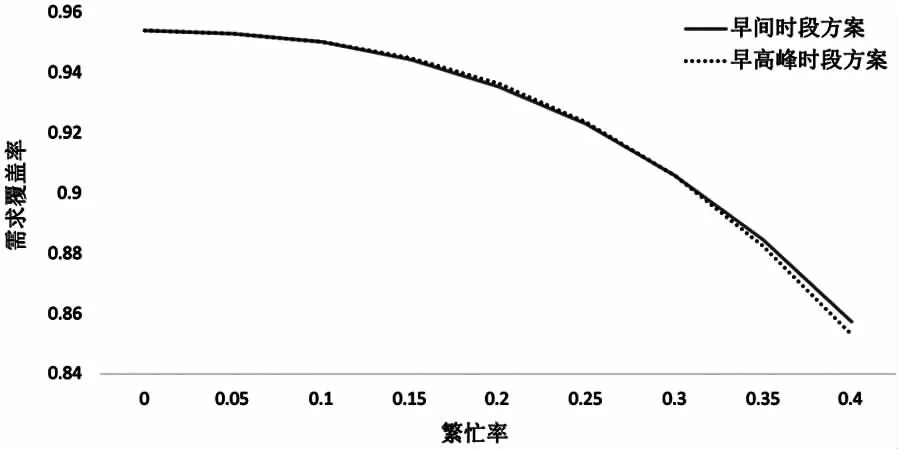
图2 需求覆盖率与繁忙率的关系图

明显可以看出，需求覆盖率曲线随繁忙率q的增加而减小，意味着救护车处于待命时间的比例越小，其可服务的需求越少，这与实际意义完全相符。同时也可以看出，在0＜q≤0.3时，两种布局方案下的需求覆盖率具有很小的差异。这表明在繁忙率低于0.3的情况下，当遇到突发状况导致无法按原计划对救护车进行再布局时，对需求覆盖率的影响在可接受范围内。

5 结论

本文针对院前急救中救护车布局问题，通过引入繁忙率的概念，对传统的双覆盖模型加以改进，并将模型应用于上海市松江区，基于已有站点对救护车进行合理布局，验证了改进后模型的优越性，具有较强的可行性与应用性。同时，为了更贴合实际，考虑到一天中不同时段救护车繁忙率的差异，本文提出了多时段布局方案，以“早高峰”和“晚高峰”为界点，将一天划分为5个时段，通过本文模型得到5个时段下分别的最优布局方案，保证了期望覆盖需求量的最大化，更利于决策者做出合理决策。最后，本文验证了繁忙率与需求覆盖率之间的关系，即繁忙率越大，需求覆盖率越小。需要指出的是，本文假设救护车行驶速度是恒定的，在今后的研究中可以考虑多时段下救护车速度的不同，使研究结果更为精准。也可以从救护车响应急救需求时间的角度考虑问题，保证需求被快速响应。在本文多时段布局的结论基础上，也可以根据救护车布局方案，进一步探究救护车工作人员的排班情况。这些都是未来研究中可以考虑的研究方向。

院前急救服务能力可以体现出一座城市，乃至一个国家的急救医疗水平与社会安全保障程度。虽然近年来，我国的院前急救服务水平已经得到了很大的提升，但由于起步晚、基础弱等历史原因，较之于西方发达国家，我们的服务水平还处于相对落后的状态。因此，要进一步加快和保障急救系统健康发展，提升急救服务水平与应急救援能力，为创造和谐社会提供有力的保障。