基于韧性度的低轨卫星通信网络抗毁性度量及优化

邵瑞瑞， 方志耕， 刘思峰， 游伟青， 聂媛媛， 高 素

（1.南京航空航天大学 经济与管理学院，江苏 南京211106；2.江苏省国家密码管理局，江苏 南京210013；3.中国空间技术研究院 通信卫星事业部，北京100094）

0 引言

我国疆土辽阔，自然灾害较多，经济发展迅速但发展很不平衡，同时面临着严峻的国内外安全及治安形势。虽然电信业在近年来得到飞速发展，但是受地理环境和经济因素的制约，地面通信网络只覆盖了国土面积的约15%，且在重大自然灾害的抢险救灾、远海、高纬度地区没有通信能力，全球范围的维和、救援以及科学考察、资源运输等缺乏主导的通信网络，信息安全问题存在重大隐患，建立我国自主可控的卫星移动通信系统成为亟需解决的问题［1］。低轨道（Low Earth Orbit，LEO）卫星移动通信系统具有信号传播距离短，链路损耗和传播时延小，采用蜂窝通信、多址、点波束、频率复用等相对比较成熟的技术，实现了真正意义的全球覆盖［2］。因而，低轨卫星通信将成为未来卫星移动通信的主要发展方向。卫星通信网络与传统的地面通信网络相比，在应用场景上有很大的不同，卫星布置在轨道面上有其自身的工作寿命，与此同时还可能受到外界的攻击，其外部环境相对苛刻，使得其抗毁性的研究成为低轨卫星通信网络技术的核心问题。

网络抗毁性是指网络中的节点或边发生自然失效或遭受故意攻击时，网络拓扑结构保持连通的能力［3］。在低轨卫星通信中，用无向连通图来表示通信网络，图的顶点代表低轨卫星星座中的卫星节点，边代表无线通信链路。在此数学模型下，人们开始讨论抗毁性的有关测度。众所周知，网络的抗毁性与其连通性有十分密切的关系，因而早期的研究主要集中在对图的点连通度和边连通度这两个参数的分析［4］。而连通性仅描述了网络遭受破坏的难易程度，而没有考虑网络被破坏后剩余网络的连通能力。鉴于此，一些新的抗毁性参数被引入来解决这一困难，如坚韧度、离散数、完整度、韧性度［5～8］。文献［8］提出的韧性度指标综合了网络被破坏的难易程度、被破坏后连通分支的规模、数目，更精细地度量网络的抗毁性。孙成雨等［9］提出韧性度作为网络抗毁性的指标，利用改进二进制粒子群算法求解点韧性度，验证了方法的有效性。在网络的抗毁性研究中，低轨卫星通信网络必须考虑节点移动和切换造成的影响，这就为低轨卫星通信网络抗毁性的研究提出了新的挑战。彭兴钊等［10］考虑了加权网络在不同攻击策略下的级联抗毁性，分析了随机攻击与恶意攻击下的网络抗毁性问题。蒋瑞［11］研究了星上路由策略，提出切换是影响系统整体性能的关键因素，通过信道预留与接入控制策略来降低通话中断的概率。Matar EDH等［12］开发了一个分析框架，用于评估完全共享（CS）与低地球轨道-移动卫星系统（LEO-MSS）中多类业务的两种不同切换优先级方案的性能，开发了保护信道和切换请求方案排队的组合。Mirzasoleiman B［13］等在加权网络中研究了级联故障的容差，考虑了三种加权策略对链路负载、网络性能的影响。

从已有的抗毁性文献可以看出，低轨卫星通信网络抗毁性的研究主要集中在不同攻击策略、路由策略和链路容量的优化设计上，并且都是考虑无权或者边加权某个时刻的抗毁性，在考虑某个时间段内的抗毁性及其改进的问题上显得明显不足。本文通过考察网络抗毁性的一个良好参数韧性度，结合低轨卫星的移动与切换模型来度量低轨卫星通信网络在某个时刻及某个时间段的抗毁性，与此同时通过对切换模型中关键信道的赋权，求得了赋权韧性度下的抗毁性，实现了对低轨卫星通信网络抗毁性的度量与优化。

1 相关理论

低轨卫星通信系统（简称LEO星座系统）主要是指轨道高度小于5000千米的一组或一群卫星相互协同工作，共同提供通信服务的卫星通信系统［14］。卫星轨道的形状和高度对卫星星座的覆盖性能有非常大的影响，是确定完成对指定区域覆盖所需的卫星数量和系统特性的一个非常重要的因素。按照卫星轨道的形状分为圆轨道和椭圆轨道，从轨道倾角的角度出发，卫星轨道分为赤道轨道、极地轨道和倾斜轨道。从轨道高度的角度出发，可以将卫星轨道分为低地球轨道LEO（Low Earth Orbit）、中地球轨道MEO（Medium Earth Orbit）、静止/同步轨道GEO/GSO（Geostationary/Geosynchronous Orbit）和高椭圆轨道HEO（Highly Elliptical Orbit）。

低轨卫星通信网络的抗毁性需要考虑卫星的移动、星间链路的不断切换带来的影响，确保网络的连通性和关键功能。当网络遭受攻击时，拓扑结构随时可能变化，要求其仍然能够完成必要的通信任务。抗毁性模型中相关参数及理论定义如下：

定义1韧性度（Cozzens等人［8］）

设G（V，E）是一个无环无重边的简单图，V为顶点集，S为割点集，S⊆V，E为边集。

其中，割点是指在图G中删去一个节点S后，图G的连通分支数增加，即ω（G-S）＞ω（G），则节点S为G的割点。｜S｜表示割点集S中节点的数量，G-S表示图G去除割点及其边后剩余的图，ω（G-S）表示G-S的连通分支数，τ（G-S）表示G-S最大连通分支的顶点数。

定义2赋权韧性度

设（G，W）是一个点赋权完全连通图，其赋权韧性度定义为：

其中，τW（G-S）表示G-S各连通分支顶点权和的最大值，W（S）＝ΣW（v）。

2 基于韧性度的低轨卫星通信网络抗毁性模型构建

2.1 建模思路和原理

在设计低轨卫星通信网络的时候，为了保证其有效运行，设计者既要考虑网络内部节点发生失效或在受到攻击时能维持通信要求不易被破坏，又要考虑一旦网络遭到破坏后能够容易修复而承受较小的代价。卫星在轨道内高速移动，为了确保通信的连续性必须进行切换，包括波束切换、卫星切换以及星间链路的极区切换，卫星的移动和切换是实现低轨卫星通信的关键因素。

通过对低轨卫星移动的分析得到其移动模型，进而求得其简化拓扑结构图为Gx，Gy，…，同理，通过对卫星切换模型的分析得到其简化拓扑结构图为Gu，Gv，…，进而对某时刻的抗毁性以及某一段时间内的平均抗毁性进行度量。因此，低轨卫星通信系统抗毁性的建模可以通过对卫星的移动和切换模型分析，对抗毁性进行度量及优化的过程，如图1所示。

图1 低轨卫星通信网络抗毁性建模

2.2 低轨卫星通信网络的移动模型

不同的移动模型对网络的性能、网络的运行成本以及网络的安全性都会产生不同的影响。对移动模型的研究和分析有助于整个卫星星座的设计，对卫星通信网络的安全性及韧性度、抗毁性等性能的改善起到推动作用。因此，分析低轨卫星通信网络的移动模型以及如何度量不同移动模型的抗毁性，是卫星星座设计和实现网络通信所要考虑的首要问题。

卫星的移动遵循特定的轨道，根据轨道中的卫星间是否存在星际链路分为有星际链路卫星星座（Iridium系统）和无星际链路卫星星座（Globalstar系统、Teledesic系统）等。所谓星际链路，是将星座系统中相邻卫星连接起来的通信链路，使卫星有机地联系在一起。星际链路的建立使得系统可单独组网，降低了对地面网络的依赖，成为全球移动通信系统不可替代的重要组成部分，引起了世界各国的广泛关注，也是我国未来卫星通信网络的重要组成部分［15］。

簇首移动模型（Cluster head movement model，CH2M）是卫星群构成的星座围绕地球按预定的轨道周期性的运行，如果将每个轨道面看成一个簇，且每个簇存在一个簇首卫星，簇首卫星的特性代表了整个轨道卫星的移动行为。因此，可以看成簇首卫星带着本簇的卫星在预定的轨道内围绕地球运动。CH2M模型的卫星移动情况如图2和图3所示，其特点如下：

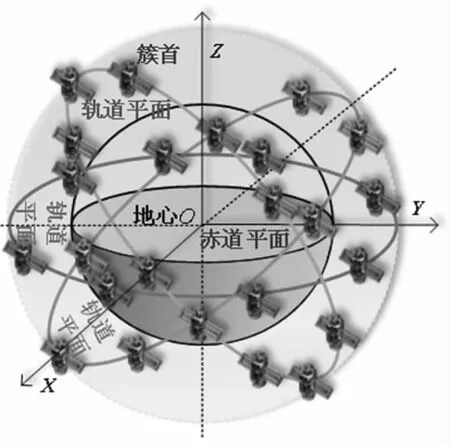
图2 卫星移动模型

图3 卫星位移示意图

（1）当簇首在轨道平面内运动时，会将相应的移动参数通过星际链路传递给周围的卫星。若簇首发生位移A→C，B→D，簇首的移动方向即由加上位移矢量得到新的位移方向

（3）同一轨道平面内的相邻卫星要保持一个安全距离SD（safe distance），即∀i，∀j，∀t，Dij（t）≥SD。

Manhattan移动模型（曼哈顿移动模型）是根据纽约市曼哈顿岛的城市地图抽象而来的，具有规则的格状拓扑结构。在该模型下，假定节点随机分布于城市街道中，城市的街道由一些水平和垂直的街道组成，并且节点只能在水平和垂直的街道上移动。由于与星座网络的拓扑结构非常类似，因而可以用来描述卫星网络的移动情况，如图4所示。

图4 星座网络的曼哈顿移动模型

2.3 低轨卫星通信网络的切换模型

在LEO卫星通信系统中，卫星在预定的轨道内绕着地球高速的公转，同时地球在自转、用户在移动。由于卫星的运动速度远高于地球的自转和用户的移动速度，成为引起呼叫切换的主要因素，用户可视为相对“静止”状态。在陆地蜂房网中，基站是静止不动的，切换主要是由于移动用户的无规律运动，而在LEO卫星通信系统中，卫星起到了类似基站的作用，切换主要归因于“基站”有规律的运动。由于两种网络中引起切换的因素与规律不同，因而不能用陆地蜂房网切换模型来分析LEO卫星通信系统的切换问题，必须建立适用于低轨卫星通信网络的切换模型。

低轨卫星星座中的切换可分为波束切换（图5）、卫星切换（图6）和星间链路的极区切换（图7）三种［16］。卫星在跨越极点时，相邻轨道面之间的卫星相邻关系产生交错，必须关闭轨道面间ISL和部分波束，导致星座网络拓扑结构发生变化。

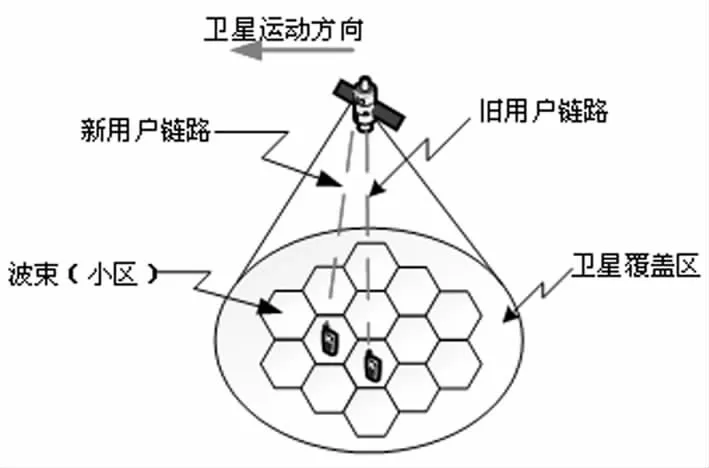
图5 波束切换

图6 卫星切换

图7 极区切换

在低轨卫星通信网络中，卫星和地面移动终端之间的相对运动，使得部分呼叫在通信过程中需跨越边界，此时系统必须将这类呼叫切换至相邻的、具有空闲信道的卫星继续服务。当空闲的信道同时接收原始呼叫和切换呼叫时，它们获得信道服务的机会是等可能的。当所有的信道都处于繁忙状态时，到达的切换呼叫不能被分配信道，对于用户而言则表现为通话中断，因而，低轨卫星通信网络切换失败的概率等于呼叫阻塞的概率。在移动通信系统中，除了通话结束信道被释放外，由于卫星运动造成单元小区不再覆盖当前用户，用户呼叫被迫切换，先前占用的信道也将被强制释放，切换状态转移图如图8所示：

图8 低轨卫星通信网络切换状态转移图

其中，Ei表示信道的占用情况，λt与μc表示切换状态的呼叫到达率，N为信道总数。当所有信道均被分配完毕后，新的原始呼叫与切换呼叫被会被阻塞。

2.4 低轨卫星通信网络抗毁性的求解

抗毁性（Invulnerability）是指系统在失效的情况下，能够继续保持正常工作的能力。沿用美国国土安全部的概念，韧性（Resilience）可以定义为系统预防和适应变化条件，并且承受这些扰动并迅速恢复的能力［17］。Francis与Bekera等对现有韧性定义的总结，认为“抵御能力、吸收能力与恢复能力”是韧性系统的三个主要特征［18］。抵抗扰动及扰动后的恢复能力是韧性理念的两个核心指标，可以说，一个系统的韧性越强，其抵御扰动、面临打击时的抗毁性也越强。与此同时，在文献［8］和［9］中都提出韧性度作为一种新的抗毁性参数，对于解决抗毁性仅注重网络遭受破坏后的连通性这一难题提出了新的解决方案。因此，本文引入韧性度来度量低轨卫星通信网络的抗毁性。

在低轨卫星通信网络中，卫星按照一定的轨道周期高速移动，为了保持通信的连续性，需要不断的进行切换，不停的移动需要不断的切换，移动与切换伴随了低轨卫星通信的全过程。如果将卫星的移动看成0时刻，切换看成T时刻，通过对移动和切换模型的分析，对［0，T］内低轨卫星通信网络的抗毁性进行度量。

在［0，T］内，做以下两点假设：

a）若低轨卫星通信网络在t时刻的移动／切换模型有n种（G1，G2，…，Gn），每种移动／切换模型出现的概率为P1，P2，…，Pn，且P1+P2+…Pn＝1。以此类推，网络在其它时刻也有类似的特点，且整个网络是保持连通的。

b）对于韧性度的求解只考虑节点（卫星）出现故障的情况。

根据上面的假设，可以求得由N个卫星组成的低轨卫星通信网络G在时刻t时的抗毁性：

其中，p1，p2，…，pn为低轨卫星通信网络G在t时刻每种移动／切换模型出现的概率，T（G1），T（G2），…，T（Gn）为低轨卫星通信网络G在t时刻移动／切换模型为G1，G2，…，Gn时的韧性度。

低轨卫星通信网络G在［0，T］内的平均抗毁性为：

由式子（3）可知，某时刻低轨卫星通信网络的抗毁性与该时刻的韧性度有关，而韧性度值跟该时刻的移动／切换模型有关。由于移动／切换模型的出现的可能性不同，因而在考察其抗毁性时引入了每种移动／切换模型出现的概率。式（3）求得的抗毁性值K（G）t越大，网络的抗毁性就越强。式（4）是某时间段内的平均抗毁性越大网络抗毁性就越强。

2.5 低轨卫星通信网络抗毁性的优化

通过对低轨卫星通信网络切换模型的分析可知，在繁忙的信道环境下，原始呼叫和切换呼叫都不能被分配信道，已经接入的用户呼叫也会中断，这显然与用户通信要求是相背离的。因此，需要对低轨卫星通信网络的切换模型进行优化，减少切换的阻塞概率，尤其应避免已经建立的通话被中断。

在优化切换模型中，通过对低轨卫星通信网络切换模型韧性度的求解，找出使网络的韧性度值达到最大的割点集所在的节点（假设有Nq个，且Nq∈［2，n-2］）为关键信道，将其专门用于分配切换呼叫。与此同时使用排队门限和定义缓冲区对切换呼叫进行先入先出的队列管理，通过缓冲区的设置达到延长呼叫切换等待时间，增大切换成功的概率，在此主要通过对信道进行赋权来体现其改进。要想赋权信道发生堵塞，对于攻击者来说要花费更高的代价。剩余的N-Nq个信道按原切换模型进行分配，当原始切换和切换呼叫到来时，首先分配N-Nq个信道，当N-Nq个信道被分配完毕后，切换呼叫到达时，使用Nq个专用信道，不再向原始呼叫分配信道。优化切换状态转移图如图9所示：

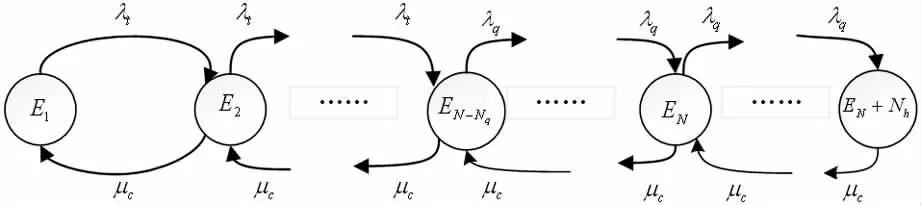
图9 低轨卫星通信网络优化切换状态转移图

其中，λt与μc表示呼叫到达率，λq表示切换到达率，N为信道总数，状态Ei表示信道占用情况和队列容纳情况，Nh表示缓冲等待队列中切换呼叫的数目。

低轨卫星通信网络的数据传输是依靠卫星节点来实现的，若网络中存在核心卫星节点，如网络割点，一旦这些卫星节点失效，将会严重影响通信网络的整体连通度，甚至导致整个网络的崩溃。因而，对切换模型的优化，可以通过对核心节点进行保护来提高网络的抗毁性。对低轨卫星通信网络优化的切换模型进行赋权，用赋权韧性度的值代替式（3）中的韧性度求得抗毁性值，进而根据式（4）求得平均抗毁性值。

3 案例分析

铱星（Iridium）是典型的低轨卫星移动通信系统，是美国Motorola公司于1986年提出的世界上第一个全球覆盖的卫星通信系统。铱星系统主要由空间段和地面段组成，空间段是指卫星星座，包含6个轨道高度为780km的近极轨道面，每个轨道面11颗卫星，共有66颗卫星以及6颗备份星。地面段主要包括系统控制中心、关口站和用户终端等。为了实现随时随地的个人通信并使卫星及其空中网可以独立于地面的蜂窝通信网络，铱星系统采用了具有星上交换功能的智能卫星，每一颗卫星都与其它卫星之间维持着星际链路ISL（Inter-Satellite Links）。星际链路ISL又分为不同轨道平面间星际链路（InterlSL）和同一轨道平面内星际链路（IntralSL），实现了真正意义上包括两极地区的全球覆盖。

3.1 铱星系统移动模型分析及其拓扑图的构造

簇首移动模型（CH2M）中，每个轨道平面内的卫星以簇首为参照进行移动，卫星之间通过交互信息进行通信，而且这些卫星在当前时刻以某种方式相连着，下一时刻还是以类似的方式相连着。在铱星系统中，每个轨道面上11颗卫星等间距分布，其中，每个轨道面都是穿过极地的圆形轨道，轨道面倾角为86.4度，卫星通过轨道平面内的星际链路（IntralSL）互连。同一轨道面上，前后2颗卫星之间的星间链固定安全距离为4033km，且每个轨道面上有一颗备份星，那么在某个时刻卫星与卫星之间的连通关系可以用图10来表示。

曼哈顿移动模型（Manhattan）模拟车辆、行人在Manhattan街道上移动的情况，其运动受到街道的限制，同一街道上的节点可以进行通信，不同街道间节点的通信要通过街道与街道交叉处节点的转发进行通信。这与铱星系统中不同轨道平面间星际链路（InterlSL）有相似之处，所以该模型下某时刻的铱星系统卫星之间的通信可以用图11来表示。

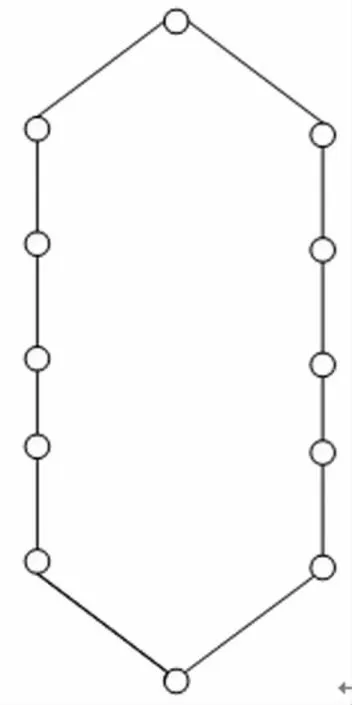
图10 铱星系统CH2M简化拓扑图

图11 铱星系统Manhattan移动模型下的简化拓扑图

3.2 铱星系统切换模型拓扑结构分析

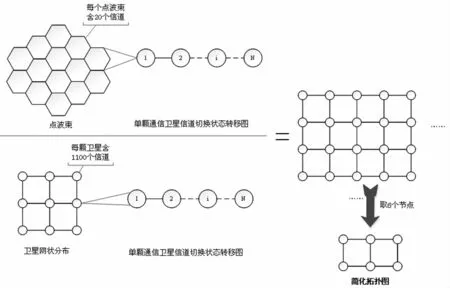
图12 铱星系统切换模型静态逻辑拓扑结构

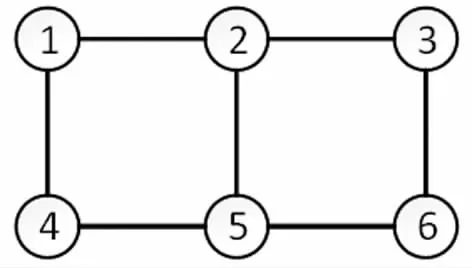
图13 铱星系统波束切换和卫星切换简化拓扑图

图14 铱星系统极区切换网络拓扑图

3.3 铱星通信网络的抗毁性

在铱星通信网络中，在t＝0时刻的移动模型拓扑结构如图10和图11两种情况，其分别代表卫星在同一轨道平面内星际链路（IntralSL）和不同轨道平面间星际链路（InterlSL）上移动，在此认为其出现的概率相同。在t＝1时刻的波束切换和星间切换的拓扑结构为图13所示，星间链路的极区切换如图14所示，并且铱星卫星的轨道周期约100min，波束平均切换时间为1～2min，星间切换的时间平均为9min，星间链路切换时间间隔为162.69s和111.26s［21～23］。据 此 设 波 束 切 换 出 现的概率为0.57，星间切换出现的概率为0.08，星间链路的极区切换出现的概率为0.35。

根据2.4中提出的度量方法计算铱星系统在通信时的抗毁性以及平均抗毁性值。

a）先考虑t＝0时刻铱星通信网络的抗毁性：

根据式（1）可以求得图10和图11的韧性度分别为：T（G）t＝0＝3.5，T（G）t＝0，且p1＝

由式（3）可 得：K（G）t＝0＝p1T（G1）t＝0+

b）再考虑t＝1时刻铱星通信网络的抗毁性：

c）根据求得的低轨卫星通信网络在t＝0，t＝1时刻的抗毁性值，根据式（4）可以求得此网络在［0，1］内的平均抗毁性值：

（2）操作阶段。操作阶段包括以下任务：第一，为知识客户提供知识搜索请求的终端用户界面；第二，选择与用户请求相关的知识源进行知识源网络配置；第三，对已有的知识和生成的知识进行选择、获取、融合以及确认；第四，为用户提供请求结果；第五，存储请求结果。

3.4 铱星通信网络抗毁性的优化

图13铱星系统波束切换和卫星切换简化拓扑图韧性度的求解过程及结果如表1所示。由于南北极地区人口资源少，铱星系统卫星覆盖密集，且星间链路的极区切换导致星座网络拓扑结构处于快速的变化中，为了简化模型，在此仅对波束切换和卫星切换方式进行优化。

铱星通信网络的优化步骤如下：

步骤1通过对铱星通信网络切换模型韧性度的求解筛选出Nq个关键信道；

步骤2将Nq个关键信道首先用于确保切换呼叫，同时使用排队门限和定义缓冲区对切换呼叫进行先入先出的队列管理，为体现这些措施实现的效果，主要通过对对信道进行赋权；

步骤3度量赋权韧性度下铱星系统的抗毁性。

表1 铱星系统切换模型的韧性度

韧性度的大小反映网络的抗毁性。从表1可知，当割点集为②⑤时，计算出的铱星系统切换模型的韧性度值达到最大，此时铱星通信网络的抗毁性强，切换呼叫的成功率自然就高，如果将②⑤作为呼叫切换的专用信道，当专用信道遭受攻击时对铱星系统的造成的影响也是最小的。对表1中的所有割点集统计各个节点出现的次数，如表2所示。从表2可知，②⑤一旦遭到破坏，对铱星系统的连通性影响最大，因而将②⑤作为N-Nq个信道全部分配完的补充信道，仅用于提高切换呼叫的成功率是合理的。

表2 所有割点集中各个节点出现的次数

现将②⑤专门用于切换呼叫信道，并使用排队门限和定义缓冲区对到来的切换呼叫进行先入先出的队列管理，为了更形象地体现切换呼叫的优化效果，通过节点赋权实现对铱星通信网络抗毁性的优化。

所有割点集中各个节点出现的次数说明了节点的重要程度，为了提高网络的抗毁性，在设计阶段需要对重要的节点采取保护措施（如备份等），因而想要破坏它需要付出更大的代价。按照表2节点在割点集中出现次数的排序结果，同时结合切换呼叫的优化效果，对图13铱星系统切换模型的赋权如图15所示。

图15 铱星系统优化切换模型赋权图

3.5 仿真分析

对低轨卫星通信网络的抗毁性模型，用Matlab来分析此模型中韧性度对某时刻抗毁性值的影响，用origin对铱星通信系统优化前后的抗毁性及平均抗毁性进行了对比，如图16所示。

当低轨卫星通信网络在［0，T］内的简化拓扑结构只有n＝1种时，该网络在t时刻的韧性度与抗毁性的关系如图17所示。

图16 铱星通信网络优化前后对比

图17 t时刻韧性度与抗毁性的关系

由图16易知，通过对铱星通信系统切换模型的优化，网络的抗毁性与平均抗毁性都得到了提升。根据图17可知，当低轨卫星通信网络只有一种拓扑结构时，任意时刻网络的抗毁性跟拓扑结构的韧性度值有关，并且是一种线性关系，即随着韧性度的增加，其抗毁性也增加。由于每个时刻的韧性度与抗毁性是一种线性关系，平均抗毁性是通过各个时刻抗毁性总和的平均数求得，所以平均抗毁性也是随着韧性度的增加而增加，与韧性度也是一种线性关系。

4 结论

本文主要研究了低轨卫星通信网络的抗毁性，提出一种基于卫星移动和切换为主导因素，通过韧性度的求解对某时刻的抗毁性以及某时段的平均抗毁性进行度量。首先分析了低轨卫星的移动模型和切换模型，然后构建了低轨卫星通信网络抗毁性的求解模型，最后通过对切换模型的优化实现了对模型的改进，达到优化网络抗毁性的目的。铱星通信网络的实例表明，本文构建的模型不但可以对铱星通信网络某时刻以及某时段的抗毁性进行度量，而且可以通过对关键信道的识别以及信道赋权优化网络抗毁性，验证了该模型的有效性，为抗毁性的度量与优化问题提供了新的解决思路。