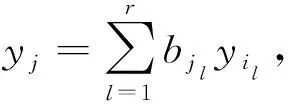一类非交换n-李代数的结构

白瑞蒲, 吴婴丽

(河北大学 数学与信息科学学院, 河北 保定 071002)

1 引言与预备知识

目前, 关于多元李代数分类的研究已有很多结果： 文献[1-3]研究了多元李代数的结构; 文献[4-6]分别对特征2域上(n+1)-维n-李代数及特征零域上(n+2)-维n-李代数和度量n-李代数进行了分类, 证明了不存在特征2域上单的(n+2)-维n-李代数; 文献[7-8]从n-李代数的生成指标出发, 对具有生成指标为n的n-李代数进行了分类. 本文主要研究特征零域F上β(L)=m-n+1的m-维非交换n-李代数[9-10]的结构, 并对具有特殊导代数维数的n-李代数进行分类, 其中β(L)是非交换n-李代数L的Abel理想的最大维数[11].

n-李代数L[9]是域F上具有线性运算[,…,]:L∧n→L的线性空间, 且对任意x1,…,xn,y2,…,yn∈L, 满足下列恒等式:

设L是n-李代数,A是L的子空间, 若A满足[A,…,A]⊆A([A,L,…,L]⊆A), 则称A为L的子代数(理想)[10]. 若[A,…,A]=0([A,A,L,…,L]=0), 则称A为L的交换子代数(Abel理想). 特别地, 由[x1,…,xn]生成的子代数称为L的导代数, 记为L1, 其中x1,…,xn为L中的任意元素. 若L1≠0, 则称L为非交换n-李代数.Z(L)={x∈L|[x,y1,…,yn-1]=0, ∀y1,…,yn-1∈L}称为L的中心. 显然,Z(L)是L的Abel理想. 设L为非交换的n-李代数, 记β(L)为L的Abel理想的最大维数.

引理1[11]设L为m-维非交换n-李代数, 则m≥n,β(L)≤m-n+1, 且当β(L)=m-n+1时,L1⊆I, 其中I是任意满足dimI=β(L)的Abel理想.

本文规定F是特征为零的域,L是F上的n-李代数,I是L的具有最大维数的Abel理想, 对S⊆L, 记〈S〉为S张成的子空间.

2 主要结果

2.1 dim L1=1时n-李代数的分类

定理1设L为m-维n-李代数, 且β(L)=m-n+1, dimL1=1, 则dimZ(L)=m-n, 且在同构意义下有且仅有如下两类: 1) [x2,xm-n+2,…,xm]=x1; 2) [x1,xm-n+2,…,xm]=x1. 其中{x1,…,xm}为L的一组基.

证明: 由引理1可知L1⊆I. 设{x1,…xm}是L的一组基, 其中x1,…,xm-n+1∈I,L1=Fx1, 则有

L1=[L,…,L]=[I,xm-n+2,…,xm]=Fx1.

如果L1⊆Z(L), 不妨设[xi,xm-n+2,…,xm]=λix1,λi∈F,λ2=1, 2≤i≤m-n+1. 做x1,…,xm的基变换, 将xi置换成xi-λix2, 则有[xi,xm-n+2,…,xm]=0,i≥3, 得到1), 并且Z(L)=〈x1,x3,…,xm-n+1〉, 因此dimZ(L)=m-n. 如果L1Z(L), 不妨设[xi,xm-n+2,…,xm]=λix1,λi∈F,λ1=1, 1≤i≤m-n+1. 同理讨论可得2), 并且Z(L)=〈x2,…,xm-n+1〉, dimZ(L)=m-n. 根据L1是否含于Z(L)可知1)与2)不同构. 证毕.

2.2 dim L1=2 时n-李代数的分类

定理2设L为m-维n-李代数, 且β(L)=m-n+1, dimL1=2, 则dimZ(L)=m-n-1, 且在同构意义下有且仅有如下几类：

其中{x1,…,xm}为L的一组基.

证明: 由引理1可知L1⊆I. 设{x1,…,xm}为L的一组基, 且I=〈x1,…,xm-n+1〉,L1=〈x1,x2〉. 下面分3种情形讨论:

(i)L1⊆Z(L). 此时[x1,L,…,L]=[x2,L,…,L]=0. 不妨设[x3,xm-n+2,…,xm]=x1+μx2, [x4,xm-n+2,…,xm]=λx1+x2, [xi,xm-n+2,…,xm]=λix1+μix2, 其中λ,μ,λi,μi∈F, 5≤i≤m-n+1. 做x1,…,xm的基变换, 将x1,x2,xi分别置换成x1+μx2,λx1+x2,xi-λix3-μix4, 5≤i≤m-n+1, 则有[xi,xm-n+2,…,xm]=0,i≠3,4, 得到1), 并且Z(L)=〈x1,x2,x5,…,xm-n+1〉, dimZ(L)=m-n-1.

(ii)L1Z(L)且L1∩Z(L)=Fx1. 此时[x2,xm-n+2,…,xm]≠0, 不妨设

(iii)L1∩Z(L)=0. 此时[x1,xm-n+2,…,xm]与[x2,xm-n+2,…,xm]为线性无关的向量. 设A=〈x1,x2,xm-n+2,…,xm〉, 则A是(n+1)-维子代数, 且dimA1=2. 由文献[5]中定理3.2可知, 在同构意义下A仅是如下情形之一:

与上述讨论类似可知, 当A分别为情形①,②,③时,L分别同构于4),6),5), 且Z(L)=〈x3,…,xm-n+1〉, dimZ(L)=m-n-1. 证毕.

2.3 dim L1=3时n-李代数的分类

定理3设L为m-维n-李代数, 且β(L)=m-n+1, dimL1=3, 则dimZ(L)=m-n-2, 且在同构意义下有且仅有如下几类:

其中{x1,…,xm}为L的一组基.

证明: 假设I=〈x1,…,xm-n+1〉为L的(m-n+1)-维Abel理想, 则L=I〈xm-n+2,…,xm〉, 且L1=[I,xm-n+2,…,xm]⊆I. 不妨设L1=〈x1,x2,x3〉.

(ii)L1Z(L)且dim(L1∩Z(L))=1. 此时A=〈x1,x2,x3,xm-n+2,…,xm〉为(n+2)-维子代数, 且dimA1=2. 由文献[5]中定理3.2可知,A同构于下列情形之一:

不妨设[xi,xm-n+2,…,xm]=λix1+μix2+ηix3,λiμiηi∈F,η4=1, 4≤i≤m-n+1.

(iii)L1≠Z(L)且dim (L1∩Z(L))=2. 此时[x3,xm-n+2,…,xm]≠0, 且A=〈x1,x2,x3,xm-n+2,…,xm〉为(n+2)-维子代数, dimA1=1. 由文献[5]中定理3.2可知,A仅为如下情形:

[x3,xm-n+2,…,xm]=x1或[x3,xm-n+2,…,xm]=x3.

因此,L是如下两种情形:

(1)

(2)

如果L为式(1), 则将x2,x3,xi分别置换成x2+η4x3,μ5x2+x3和xi-λix3-μix4-ηix5, 6≤i≤m-n+2, 得到3), 且Z(L)=〈x1,x2,x6,…,xm-n+1〉, dimZ(L)=m-n-2. 如果L为式(2), 则将x1,x2,xi分别置换成x1+η4x3,μ5x1+x2,xi-λix4-μix5-ηix3, 6≤i≤m-n+2, 得到2), 且Z(L)=〈x1,x2,x6,…,xm-n+1〉, dimZ(L)=m-n-2.

由于3)的幂零性可知2)不同构于3).

(iv)L1∩Z(L)=0. 此时[xi,L,…,L]≠0(i=1,2,3)是线性无关的向量. 因此,A=〈x1,x2,x3,xm-n+2,…,xm〉为(n+2)-维子代数, 且dimA1=3. 由文献[5]中定理3.2可知,L有且仅有如下情形:

类似讨论各种情形, 分别做适当的基变换可得不同构的n-李代数9)～11), 且Z(L)=〈x4,…,xm-n+1〉, dimZ(L)=m-n-2. 证毕.

2.4 β(L)=m-n+1且Z(L)⊆L1时n-李代数L及其导代数L1的维数

定理4设L为m-维n-李代数,β(L)=m-n+1,Z(L)⊆L1, 则当dimL1=1时,n≤m≤n+1; 当dimL1=2时,n+1≤m≤n+3; 当dimL1=3时,n+2≤m≤n+5.

证明: 当dimL1=1,2时, 分别由定理1和定理2可得结论. 当dimL1=3时, 根据定理3可知, 当L是1)时,m=n+5;L是2)和3)时,m=n+4; 如果L是4)～8), 则m=n+3; 如果L是9)～11), 则m=n+2. 证毕.

定理5设L为m-维n-李代数, 且β(L)=m-n+1,Z(L)⊆L1. 如果dimL1=r, 则(m-n+1)/2≤r≤m-n+1.

证明: 假设dimZ(L)=t, 则0≤t≤r. 设{x1,…,xt,…,xm-n+1,xm-n+2,…,xm}是L的一组基, 其中I=〈x1,…,xm-n+1〉,Z(L)=〈x1,…,xt〉,L1=〈x1,…,xr〉. 不妨设