游戏，助推学生数学理解

包玲玲

摘  要：游戏的课堂，能唤醒学生思维的火花;课堂上游戏，能驱动学生挑战的欲望。文章主要对一节游戏课的课堂设计进行分层次剖析，深入问题本质进行思考，深度反思游戏课堂实施的有效性。各环节围绕课堂設计、课后反思进行阐述，目的在于表达学生在由简至难的游戏中，获取数学知识，增长数学活动体验，发散数学思维，助推数学理解。

关键词：数阵;游戏;助推;数学理解

《神奇的数阵》是一节自主开发设计的数学游戏探究课。缘何开发这节课呢？其实是受了学生喜欢的数独游戏的启发，于是翻阅了大量的资料，学习了其他教师的实践操作经验，最终以“入门场、训练营、挑战台”三部分呈现内容，形成独特的游戏课堂教材，目的在层层递进的游戏活动中，带领学生玩数学游戏，感受数阵中蕴含的数学规律。

入门场

本场游戏的难度为初级，主要针对刚入门数阵游戏的玩家而设置。

“数阵游戏”认一认：

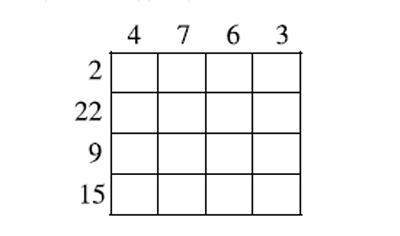
“数阵游戏”玩一玩：怎样利用8个数字设计16格数阵呢？

游戏回顾：本场挑战你过关了吗？在游戏过程中，你发现了什么窍门呢？

训练营

本场游戏的难度为中级，主要针对初学数阵游戏的玩家而设置。

“数阵游戏”玩一玩：从中任意选择一个数，把它所在的行和列上面的其他数都删去，接着再选一个没有删去的数，重复同样的操作，最后留下4个数，算出这4个数的和。

“数阵秘密”找一找：

游戏回顾：在刚才的游戏过程中，你有什么新的思考和发现呢？

挑战台

同学们，如果你已经顺利通过了前两场，那么恭喜你！下面你和小伙伴一起在实战中来大显身手啦！

玩一玩1：下面的数阵是由哪些数设计出来的？这个数阵有什么秘密？

玩一玩2：设计一个数阵，从中任选一个数，把它所在的行和列上的其他数都删去，接着再取一个没有被删去的数，经过同样的几次操作后，让留下的4个数（5个数甚至6个数）的和等于100。

游戏回顾：在玩游戏的过程中，你应用了哪些巧妙的方法？

聪明是玩出来的，数字思维是训练出来的。僵化的数字只会禁锢大脑的发散与创新能力，一个习惯性拘泥于数字的人只会使大脑被动地接受信息，而主动地接受数字是培养思维能力的一个重要因素。鉴于此，教材编写后，总想在课堂实践一下，于是精心设计教学流程，通过“初步观察探究规律——第一次游戏初探规律——深层次游戏揭示规律——逆向思维体验规律”这样一个融分析、比较、概括、推理等活动于一体的过程，让学生发现数阵蕴含的规律。设计这样的数字游戏，目的在于活跃大脑中本来对数字比较敏感的思维，真正玩转数学，在自主探究、合作交流的数学游戏中，带来思维碰撞，体验“变与不变”数学思想的独特魅力，感受游戏给数学课堂带来的乐趣。

教学片段一：（入门场） 借助有趣的故事，巧妙布阵，初探规律

（1）谈话：在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，知道它是谁吗？（介绍数阵）

（2）布阵：数阵王国，对喜欢探究数字规律的人有着极大的吸引力，看，这8个数字要来布一个16格数阵（见前面“入门场”）。怎么布阵？（两个数相加）

（3）初探：这个数阵神奇在哪里呢？（行与行、列与列之间存在相差数相等的规律）

思考：这是游戏的热身区，在这里，要熟悉游戏各部件，便于游戏过程中熟练应用。于是课的开始，简单介绍数阵，了解数阵布局的方法，是非常有必要的。学生在自主尝试的布阵游戏中，用观察法探究出数阵表面蕴含的规律，从行列之间的相差数引导学生关注到数阵外的原始数，体会到数与数之间的联系，醉翁之意不在酒，自然过渡到下一个环节。

教学片段二：（训练营）巧妙设计游戏，合作探究，深寻奥秘

（1）第一次游戏：介绍完游戏规则后两人合作游戏：从16格数阵中任选一个数，然后把它所在的行和列上的其他数都删去。接着再选一个没有被删去的数，经过同样的几次操作后留下4个数，最后算出这4个数的和。（学生游戏）

（2）揭秘1：不管怎么选数，根据游戏规则，剩下4个数的和都是68。

（3）第二次游戏：为什么剩下4个数的和都是68？不着急，继续游戏。任意交换布阵8个数的位置，新布一个16格数阵，按照游戏规则算出剩下的4个数的和是多少。（学生游戏）

（4）揭秘2：剩下4个数的和还是68。

（5）激趣：这个数阵到底存在什么神奇的奥秘？（引导学生关注布阵数）

（6）解疑：不管怎么变换位置顺序，布阵8个数没有变，剩下4个数的和等于外面布阵8个数的和;其实数阵里面的每个数是这8个数中的每两个数的和。

（7）推理：要使留下的4个数的和不是68，应该怎么办？改变布阵的8个数的大小。（学生改变布阵数操作）

（8）思考：同样是改变数字，为什么第三个数阵留下的4个数的和还是68呢？（总和没有变）

思考：游戏玩到这个环节，需要熟练的技巧和成熟的方法支撑。这一环节，是课的精华，设计两次游戏操作，深入探究数阵中蕴含的规律。第一次游戏：根据游戏规则操作，数阵中留下的4个数的和都是68，学生在交流中发现神奇之处，这时有少数学生已经发现原因。第二次游戏：改变游戏规则，随便打乱布阵的8个数的位置继续游戏，数阵中留下的4个数的和还是68，这时大多数学生明白了各种原因。

两次游戏的设计，不是偶然的，是经过多次尝试实践后形成的。第一次课堂实践，只设计了一次游戏，结果是只有极个别学生明白“为什么和都是68”，于是在教师的“强牵鼻子”的问答中，学生似懂非懂，最后也就“懂”了。第二次课堂实践，设计了两次游戏，教师规定了交换数的位置，学生在两次游戏中，明白原因的学生比第一次多了，但是总觉得学生在课堂上的自主能力体现得还不够。

反复几次实践，反思回顾课堂，总是缺少点什么？于是重审本堂课设计的初衷：让学生在主动探究和合作交流的游戏课堂中，体验“变与不变”思想的魅力。那何不把课堂交给孩子，让孩子们作为游戏玩家，在课堂这个游戏场地放开手脚尽情享受游戏魅力？于是在一次次地尝试下，产生了第二次游戏的操作要求：同学们大胆交换布阵数的位置，想怎么交换就怎么交换，根据游戏规则去游戏，找到其中蕴含的规律。学生在这样的游戏要求下合作游戏，兴趣颇高，实践研究表明：改变了游戏规则后，学生的主体作用更加彰显，他们在游戏中体验、感悟，只有体验之后才能深刻感悟事情的发展过程，只有体验后的获得才是真实有效的经验。游戏操作后发现“和为什么都是68”这一规律的学生居然达到了顶峰状态，真是蓦然回首，灯火就在阑珊处啊！

教学片段三：（挑战台）逆向思维训练，自主设计，完全理解规律

（1）提问：这个数阵又有哪些神奇的地方呢？它是由哪些数设计出来的？

（2）揭示：这个数阵第四行第三个数为0，就知道与它对应的外面的两个数分别都是0，从而知道了全部布阵数。

（3）总结：抓住了解题的题眼，很快地解决了问题。

（4）探索：四人小组一起探究，合作设计一个数阵，按照游戏操作要求，让留下的4个数（或者5个数、6个数）的和等于100。

思考：这个时候，游戏玩家已经到達一定的高度，那么设计一些高难度的游戏，对玩家来说是再一次激发学习热情，挑战大脑思维强度。于是在课尾的这一环节，设计了两个层次的练习：

第一层次，出示一个25格数阵的逆向思维题，让学生找出布阵数。这个问题的抛出，对于学生来说具有一定挑战，学生在教师一步步地引导下，找到题眼，突破障碍，解决问题。课后反思此环节，发现还是存在一些问题：虽然学生在一步步引导中找出了布阵数，但是主动发现题眼的孩子还是很少，是何原因呢？反思发现，这25格数阵的逆向思维题出现得不免有些早和快，学生还沉浸在训练营的喜悦之际，突然来这么高难度的挑战，有点措手不及;如果还是在16格数阵中研究逆向思维题的话，应该会更加水到渠成。充分利用16格数阵，把规律挖透、弄实，特别是找突破口这一环节，可以从“0”这个题眼展开思维的火花，也可以从一开始的行列之间的关系入手，当然还能从游戏规则操作下剩余4个数的和反推理去解决问题，这些思考问题的方式如果在这个环节充分体现，难么这堂课的价值也就体现得淋漓尽致了。

第二层次，学生自主设计一个数阵，根据游戏规则，剩下的4个数或者5个数的和是100。这个层次的操作，实践了多次，发现在40分钟的课堂教学中根本无法完成，只能用作课后延伸，学生自主探究。这个环节却给了笔者一些启发，既然一堂课内容太丰满，那么可以把游戏课堂做成系列，采用顺藤摸瓜式地研究，从另外的角度开发数阵游戏，如两数相减、相乘之后布阵，数字之间存在什么规律？这样形成的数阵系列游戏，对学生高阶思维的训练有着举足轻重的作用。

这样一次纯游戏的数学课堂，学生倍感兴趣，课后意犹未尽，还多次问笔者下次研究什么数学游戏，看到这样的场景，倍感任重道远。游戏课堂，迎合时代需要，在这里，学生是游戏玩家，他们有足够的时间和空间充分参与游戏活动，体会数学知识的“再创造”。他们在课堂上积极参与、全身心投入，每个人都能在游戏中找到自己的角色位置，主动性、合作性、求胜性、创造性得到张扬和提升。游戏课堂，学生的学习更加有效，最可贵的是学生在游戏过程会深入思考问题，把任何一个问题，通过一层一层的分析，找到问题的本质和最底层的逻辑。