基于优化的子模函数最大化的超像素图像分割
杜 炜,马 春,汪 庆,耿英保
安徽中医药大学医药信息工程学院,安徽合肥,230012
超像素分割算法是许多计算机视觉应用中的重要模块,比如目标识别[1],图像分割[2],以及单视图的3D重建等[3-4]。目前流行的基于图论的超像素分割算法,分别是由Felzenszwalb等提出的FH方法[5],Comaniciu提出的均值漂移和分水岭算法[6]。FH和分水岭算法运算速度极快;均值漂移对局部变量很有效;但是这三种方法产生的超像素具有不规则的尺寸和形状[7]。Ren等[7]建议使用Normalized Cut(NCut)算法来进行超像素分割。Ncut算法可以产生大小相似和形状紧凑的超像素,但它的计算开销过大,分割一幅481×321的图像需要几分钟。Veksler等[8]将超像素分割描述为图割问题。文献[9]采用不同方法生成了漂亮的棋盘花纹图像,但都是通过牺牲精细的图像细节来追求平滑的边界。然而在图像分割时需要规范集群的大小,避免过度平滑的问题。
本文将超像素分割作为聚类问题来处理,提出一种新的聚类目标函数,包含图上随机游走熵率和平衡函数两项内容。其中熵率有助于形成紧密均匀的聚类,鼓励在感知边界上划分图像,有利于超像素仅与一个对象重叠;而平衡函数使得聚类的簇具有相似大小,减少不平衡超像素的数量。除此之外,通过聚类公式推导出一种有效的算法,证明了可以通过目标函数求解优化问题,目标函数是一个单调递增的子模函数,子模性是连续域上离散的凸性。子模函数最大化通常是NP-hard问题,本文通过贪婪算法并利用拟阵结构,在解的最优性上,得到较好的效果。近来,在传感器布置[10]和疫情检测中[11],都采用了子模函数最大化的方法。
1 基本知识
定义1X={Xt|t∈T,Xt∈V}在图G=(V,E)上随机游走,用非负相似度测量权函数w,图上随机游走模型的转移概率定义为:
pi,j=Pr(Xt+1=vj|Xt=vi)=wi,j/wi
(1)
其中wi=∑k:ei,k∈Ewi,k是顶点vi的关联权值之和,静态分布如式(2)所示。
(2)
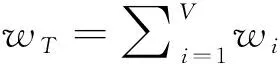
(3)
定义2令E为有限集。如果集合函数F满足
F(A∪{a1})-F(A)≥F(A∪{a1,a2})-F(A∪{a2})
(4)
且所有A⊆E,a1,a2∈E,a1,a2∉A,那么2E→R是子模块。此属性也称为递减的返回属性,表示在以后的阶段中使用模块的影响较小。
定义3对于一个集合函数F,如果对于所有A1⊆A2满足F(A1)≤F(A2),则F为单调递增集合函数。
定义4一个集合E的子集I满足以下三个条件:(1)∅∈I,(2)I∈I且I′⊆I,那么I′∈I,(3)若I1和I2属于集合,且|I1|<|I2|,然后有一个属于I1-I2的元素e,这样I1∪e∈I。则称由有限集E组成的有序对M=(E,I) 为拟阵。
2 问题描述
用图的分割方法来解决聚类问题,首先寻找一个有K个连通子图的拓扑结构,再将所提出的目标函数最大化,最终将图像分割成K个超像素块。如果一个边ei,j在聚类形成中未被选择,它的权重会被重新分配到两个顶点。使用高斯核函数将每条边旁边的数字即距离转换为相似度。每一个聚类输出都包含了不同的互相连通的集群,见图1。
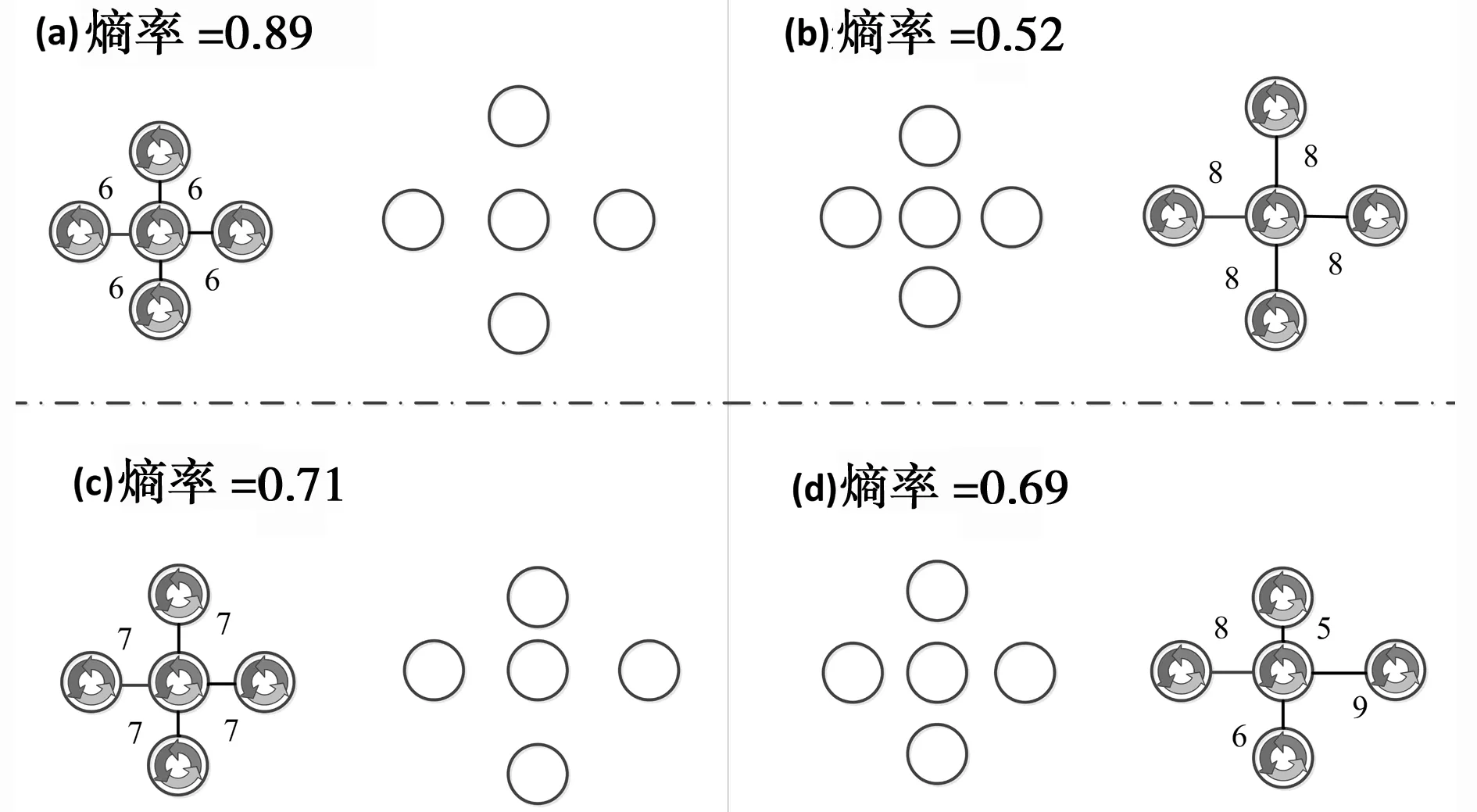
图1 熵率的作用
图1中,(a)的密集聚类的熵值比(b)中密集度较低的聚类的熵值更高。(c)中均匀聚类的熵值比(d)中不均匀聚类的熵值更高。
2.1 构 图
将一幅图片映射到图G=(V,E)上,节点表示像素,用边的权值表示成对节点的相似性,并采用相似矩阵的形式表示。选择一条边A⊆E的子集,得到图G=(V,E),且G包含了K个连通的子图。
2.2 熵 率
利用所构图上的随机游走熵率作为判别条件,得到了紧密均匀的聚类,使得图上随机游走公式(2)的静态分布保持不变。公式(5)给出了转换概率K的集合函数:
(5)
因此,在G=(V,E)上随机游走的熵率可以表示为一个集合函数:
(6)
如图1所示,尽管在集合A中包含任何边都会增加熵率值,但当选择形成紧密均匀聚类的边时,熵率值的增加会更大。在提出的图结构中,图上随机游走的熵率H:2E→R是一个单调递增的子模函数,可知熵率是单调递增的。在后面的阶段中,随着有更多边缘可以共享,那么只选择一条边带来的不确定性增幅就会降低,最终导致返回特性的递减。
2.3 平衡函数
利用平衡函数来使聚类具有相似大小。令A为选定的边集合,NA为聚类的数量,ZA是聚类的分布。例如,对于图像分割边界集合A,令SA={S1,S2,…SNA}。则ZA的分布表示为:
(7)
且平衡项表示为:
(8)
熵H(ZA)有助于使聚类具有相似大小;NA使得聚类的数量尽可能少。对于固定数量的聚类,首选采用更加平衡的分割方法。与熵率相似,平衡函数也是一个单调递增和子模块函数。所以在提出的图结构中,平衡函数B:2E→R是一个单调递增的子模块函数。目标函数结合了熵率和平衡函数,从而使得聚类更加紧密、均匀和平衡。聚类是通过优化相关边缘集合的目标函数来实现的:
(9)
λ≥0,且为平衡项的权重。非负系数线性组合保持了子模性和单调性[12]。因此目标函数也是子模单调递增的。由于目标函数是单调递增的,因此对连接子图数量的约束恰好强制为K个簇。
3 优化方法
针对上述的目标函数(9),提出了一种贪婪优化方案,采用对次模函数最大化进行优化的方法,并分析其最优性和复杂性。
3.1 高效率贪婪算法
子模函数最大化的标准方法通常采用的是贪婪算法[12]。该算法从一个空集开始(一个完全不连通图,A=∅),按顺序将边添加到集合中。每次迭代时,将产生最优增益的边添加到集合中,当连通子图的数量达到预定值时停止迭代。
为了实现算法的加速,在边缘集A上附加一个约束,使它不能含有环。此约束会忽略连接子图中的其他边,从而减少了贪婪搜索中的迭代次数,这些忽略的附加边不会改变图的分割。与原来的问题相比,尽管这个约束导致了更小的解空间(只允许树状结构子图),但实际上聚类的效果差别不大。根据无环约束和聚类个数NA≥K的约束,产生一个独立的集合定义,它包含了一个拟阵M=(E,I),定义如下所述:令E为边缘集合,I为子集A的集合,A⊆E,且A满足如下条件:(1)A满足无环设置;(2)构成A的连通子图个数大于或等于K。算法流程如图2。
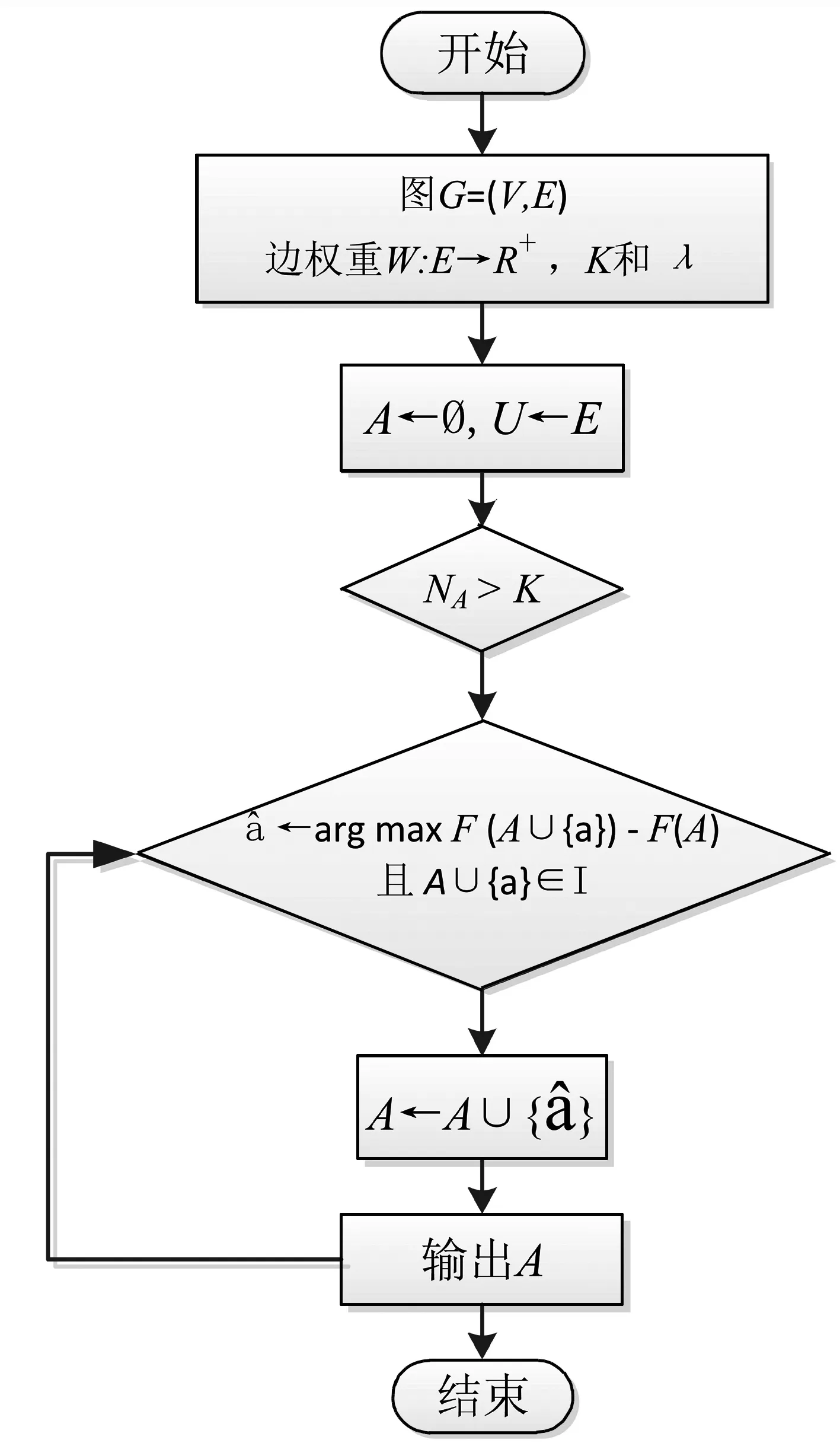
图2 高效率贪婪算法流程图
3.2 算法的有效实现
在每一次迭代中,贪婪算法在满足拟阵约束的条件下选择目标函数中增益最大的边。如图2中所述,该算法执行O(|E|)次循环将新的边添加到A中。在每次循环中,通过遍历边缘列表,找到增益最大的边,所以该算法的复杂度为O(|E|2)。
最初先计算将每个边添加到A的增益并构造一个最大堆结构。在每次迭代中,对具有最大增益的边进行出堆操作,并添加到A中。这些新添加的边会影响堆中其余边缘的增益,此时再利用子模函数的性质对堆结构进行有效更新。子模函数具有边界收益递减的性质,也就是每一条边的增益不会增加只有减少。因此,保持一个堆结构只需更新顶部增益较大的元素,而不必更新其他元素,由于堆的顶部元素已更新,则其他元素的值只能减少,因此顶部元素为最大值。
尽管此算法在最坏情况下的复杂度是O(|V|2log|V|),但实际上由于每次迭代时对堆执行的更新很少,因此平均来看,算法的复杂度近似为O(|V|log|V|),运行速度比朴素的实现算法快很多。在实验中,该算法在对大小为481×321的图像进行分割时,速度提高了50%,平均运行时间0.98秒。
4 实验和结果
超像素分割与目标分割的目标不同,因此性能指标也有所不同。本文使用三个常用的标准指标来评估超像素的质量:欠分割误差,边界回溯和可达分割精度[13]。使用G={G1,G2,…GnG}来表示一个具有nG段正确标注(GT)图像的集合,|Gi|表示段的大小。
欠分割误差率(UE) 测量超过GT图像边缘像素丢失的量。它根据超像素只能与一个对象重叠的要求来评估分割质量。这里采用Veksler等人使用的欠分割误差度量[8],公式如下:
(10)
对于每一个GT图像段Gi,可以发现重叠的超像素,并计算出的像素丢失的大小,然后将丢失像素与所有的片段相加,并通过图像大小∑i|Gi|使其标准化。
边界回溯率(BR) 测量由超像素边界恢复的自然边界的百分比。BR的计算如(11)所示:
(11)
可达分割精度(ASA)是性能上限的度量方法。对于以超像素为单位的图像分割,它可提供最高的精度。为了计算ASA,使用重叠度最大的GT图像片段的标签来标记每个超像素。这些可以正确标记的像素的片段就是可达分割精度,如式(12)所示:
(12)
这些性能指标根据图像中的超像素数量来绘制,使用的超像素数量少而产生的性能更好的算法为更优的算法。
实验均在酷睿i7处理器上运行,2.4 hz,8 G内存,其中实验1、2在Berkeley分割数据集与基准中进行,该基准包含300张带有标记的GT图像,实验3对真实自然环境下未标记的叶片图像进行超像素分割。
实验1选择两幅图像进行超像素分割实验验证。分别将两幅图像分割成128个超像素,图3对分割结果进行了直观的评价。为了更直观的可视化实验结果,将GT图像分割段用彩色编码并混合在图像上,将算法恢复的超像素边界用绿色叠加。一般情况很难注意到像素的丢失,并且超像素分割通常将图像划分为大小相似的区域,这对于基于区域的特征描述非常重要。采用随机颜色对超像进行区域填充,最后计算并绘制出超像素大小直方图。

图3 超像素图像分割实例
实验2计算Berkeley数据集中所有300张灰度图像分割指标的平均值,将文中提出的优化的子模函数最大化的超像素分割算法(MSFS)与FH、GraphCut superpixel、Turbopixels(Turbo)和NCut superpixel(NCut)四种现有分割算法的性能指标UE、BR、ASA进行了对比。
从图中可以看出,在所有的超像素点上,MSFS算法的性能在各项指标上均明显优于其他算法。图4(a)显示了欠分割误差率的曲线,MSFS在超像素计数方面优于传统算法,错误率降低了50%以上。可以实现在350个超像素的情况下仅有0.13的欠分割误差,这同使用GraphCut超像素分割技术在550个超像素的情况下具有相同的性能。MSFS在550个超像素的情况下,欠分割误差可以达到0.06。
图4(b)绘制了边界回溯率曲线。与超像素计数的其他算法相比,MSFS算法减少了30%以上的边界丢失。在超像素分别为200和600的情况下,MSFS的回溯率分别为82%和92%。在超像素计数相同的情况下,FH的回溯率为76%和86%。
图4(c)绘制了可实现的分割精度曲线。图上可以看出,MSFS该算法在所有超像素点上都能产生较好的分割上限,特别是在超像素点较少的情况下,100个超像素,ASA达到95%,而其他算法只有超像素的数量达到200时才能达到同样的精度。
实验3选择自然真实环境下叶片图像进行超像素分割,实验选择了多幅叶片图像进行超像素分割,计算边界图并将其叠加在绿色通道的输入图像上,实验结果如图5所示(在此只显示了两幅不同环境中的叶片图像),表1显示了4张叶片图像算法指标的各项参数。
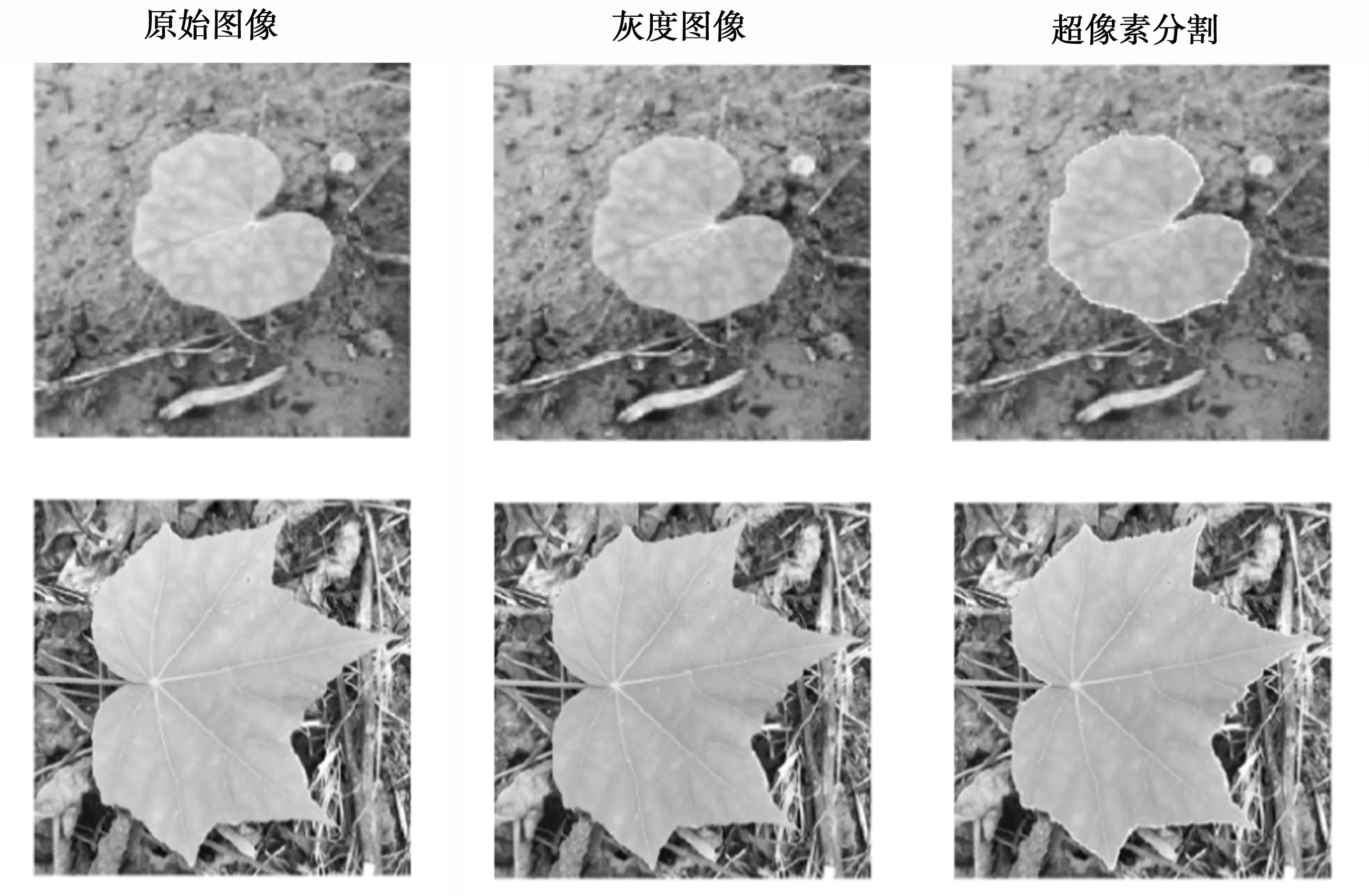
图5 自然环境下叶片超像素分割结果
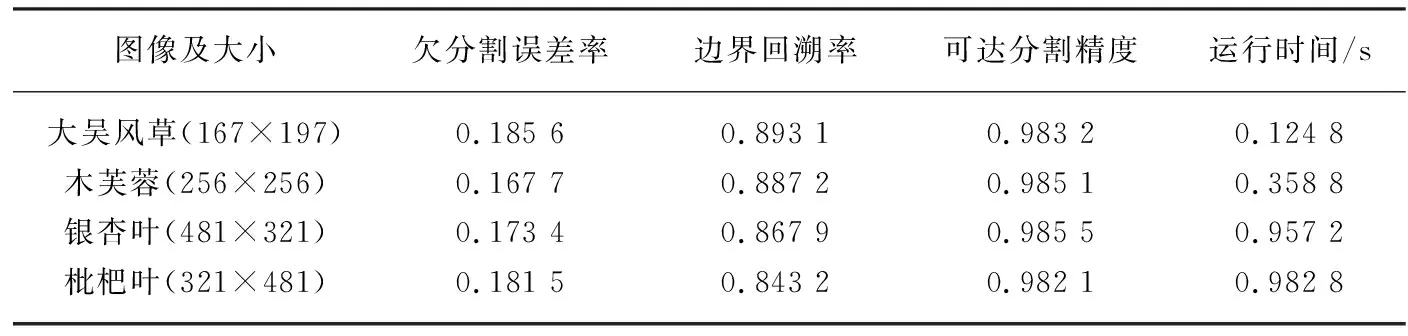
表1 真实环境中不同大小图像的MSFS算法参数对比
5 结 论
本文把超像素分割问题看作图拓扑优化问题,提出一种新的目标函数,基于图上随机游走的熵率函数,结合最优求解,推导出了一种有效的算法——子模函数最大化的超像素分割算法。通过Berkeley分割数据集与基准中的实验验证以及现实自然环境下图像的处理,表明该算法对图像的分割具有一定的现实意义。从UE、BR、ASA以及运算速度等方面与传统分割算法进行了评估和对比,具有显著的优势,欠分割误差率降低了50%,边界回溯率降低了40%,分割精度更高,算法的运算速度也明显高于其他算法,分割大小为481×321的图像只需要大约0.967 206秒。今后将计划研究此算法适用于一般的聚类问题。

