有理函数域上的最优局部恢复码的构造

陈子星

安庆师范大学数学与计算科学学院,安徽安庆，246133

现代存储系统允许几个符号丢失的情况出现，但到目前为止，单个符号丢失的情况更为常见，因此本文着重于一个符号丢失的恢复。在分布式存储系统中，一个符号丢失的恢复效率可以通过三个不同的指标来量化，分别是局部化参数r[1-4]、读取位的数量[5]、恢复带宽[6-9]，本研究关注的是局部化参数r。关于局部恢复码(LRC)的研究，文献[1]构造了一族最优的(n,k,r)LRC码，但码长受到字符集的限制，即n≤q,为了突破这一限制，文献[2]利用代数曲线来构造LRC，需要满足方程xr+1+brxr+…+b0=0，其中bi∈K(Y)，K(X)=K(Y)(x)，但过程复杂，本文利用代数函数域特别是有理函数域来构造LRC。

现代存储系统为减少存储开销，将擦除编码技术应用到系统中[10]，比起传统的通过复制提高可靠性的存储系统，更为可靠有效。本文研究的LRC码是擦除编码的一种。

1 局部恢复码的定义

就LRC而言，如果一个符号丢失，可以通过至多r个其他符号来恢复。LRC的定义如下：

定义1假设C是有限域Fq上的一个[n,k]线性码，如果对于每个i∈[n]，其中[n]:={1,2,…,n}，存在一个子集Ai⊆[n]{i}，|Ai|≤r和一个函数φi使得对于每个码字x∈C有xi=φi({xj,j∈Ai})，则称C是具有局部参数r的局部恢复码，简称(n,k,r)LRC码。

如果C是(n,k,r)LRC码,则C的信息率满足：

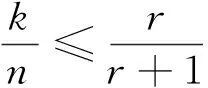
(1)

C的最小距离满足：

(2)

若(2)式成立，则称C是距离最优的(n,k,r)LRC码，当r=k时，(2)式是著名的sigleton界，若等式成立，即

d(C)=n-k+1

则称码C是MDC码。本文从代数曲线上的LRC的构造中得到启发，在代数函数域上构造LRC，特别地，在有理函数域上，得到了距离最优的LRC。

2 代数函数域上的局部恢复码

2.1 代数函数域的相关结论

定义2设一个扩域F⊇K，存在K上的超越元x∈F，使得F是K(x)上的有限扩张，则称F/K是K上单变量的代数函数域。

特别地，当K上的超越元x∈F时，若F=K(x)，则F/K被称为有理函数域。

引理1(黎曼洛赫定理) 设w是F/K的标准除子，对任意除子A∈Div(F)，有维数公式l(A)=degA+1-g+l(w-A)，若degA≥2g-1，则l(A)=degA+1-g。

引理2设一个函数域F/K和一个多项式φ(T)=anTn+an-1Tn-1+…+a1T+a0，其中ai∈F。假设存在一个位P∈PF使得以下任意一条成立vP(an)=0，vP(ai)≥vP(a0)>0，其中i=1,…,n-1，且gcd(n,vP(a0))=1。

vP(an)=0，vP(ai)≥0，i=1,…,n-1，vP(a0)<0，且gcd(n,vP(a0))=1。

则φ(T)在F[T]上是不可约的。

2.2 代数函数域上局部恢复码的构造

设F′/Fq、F/Fq均是满常域为Fq的代数函数域，F′是F的扩域且[F′:F]=r+1。若H={P1,…,Ps}是F中s个有理位的集合，对任意Pi∈H，i=1,2,…,s，在F′上都存在r+1个扩张Pi1,Pi2,…,Pi(r+1)，即对∀Pi∈H，在F′/F中是完全分裂的。

设P={Pij|1≤i≤s,1≤j≤r+1}，则|P|=s(r+1)，设A={A1,…,As}是P的划分，其中Ai={Pi1,Pi2,…,Pi(r+1)}，i=1,…,s。

设D是F上的除子且与H不相交(即SUPP(D)∩H=φ)，deg(D)=l≥1，设L(D)=〈fj|j=1,…,m〉，dim(L(D))=m。设x∈F′使得1,x,…,xr-1在F上线性无关，则定义在F′上的函数空间：

V=

定义映射

evA:V→F(r+1) sq

f(f(Pij),i=1,…,s,j=1,…,r+1)

则该映射的像为C(D,V)。

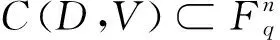
n=s(r+1)，k=rm，d≥n-(r+1)l-(r-1)h,其中h=deg(x),n-(r+1)l-(r-1)h>0。

3 有理函数域上的最优局部恢复码

下面将运用同样的构造方法来构造有理函数域上的最优LRC并修复。

设x,y都是Fq上的超越元且满足xr+1=y，其中(r+1)|(q-1)，设(q-1)=t(r+1)，设F′=Fq(x)，F=Fq(y)，则F′/Fq、F/Fq均是Fq上的有理函数域。设多项式φ(T)=Tr+1-y∈Fq(y)[T]，其中a0=-y，ai=1,…,r，ar+1=1，选取P0:=Py-0∈PFq(y)，因为vP0(1)=0，vP0(ai)=vP0(0)=≥vP0(-y)=1，因此gcd(r+1,vP0(-y))=1，所以根据引理2可知φ(T)在Fq(y)上是不可约的多项式，所以[F′:F]=r+1。

设S={P1,…,Ps}∈ΡF是F中s个有理位的集合，对任意Pi∈S，i=1,…,s，在F′上存在r+1个扩张Pi1,…,Pi(r+1)，即∀Pi∈S在F′/F上是完全分裂的。

假设0≠α∈Fq，若y=α，因为xr+1=y，则有xr+1=α，断言f(x)=xr+1-α无重根，且若αt=1，则一定存在r+1个β∈Fq使得βr+1=α。

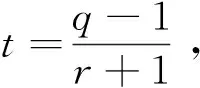
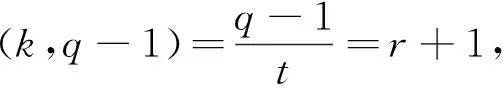
α=δk1(r+1)=(δk1)(r+1)

因此对于任意β是f(x)=xr+1-α∈Fq[x]的根，则有βr+1=α=(δk1)r+1⟹(δ-k1β)r+1=1，因为(r+1)|(q-1)则δ-k1β∈Fq，又因为δk1∈Fq，则δk1·δ-k1β=β∈Fq，因t是素数，故阶为t的有t-1个，又因为当α=1时，xr+1=α∈Fq在Fq中有r+1个不同的根，设当α1,α2∈Fq且α1≠α2时，有(xr+1-α1,xr+1-α2)=1。

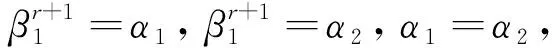
设Pα={P1,…,Pt}，取S={P1,…,Ps}⊆{P1,…,Pt}，s=|s|≤t，设F中有理位的集合为

P={Pij,1≤i≤s,1≤j≤r+1}，

则|P|=s(r+1)，设P的划分A={A1,…,As}，其中

Ai={Pi1,…,Pi(r+1)}，i=1,…,s,

设D是F上与S不相交的除子，deg(D)=l≥1，设f1,…,fm是L(D)上的一组基，因为deg(D)=l≥2g(F)-1=-1，所以

dim(L(D))=m=deg(D)+1-g(F)=l+1

因此设x∈F′，使得1,x,…,xr-1在F上线性无关，则定义函数空间

V=〈fjxi,i=0,…,r-1,j=1,…,m〉，

f(f(Pij),i=1,…,s,j=1,…r+1)，

记该映射的像为C(D,V)。

应用引理3，可以得到以下定理：

定理上述定义的码C(D,V)是Fq上的一组(n,k,r)LRC码，其参数为：

n=(r+1)s，k=rm=r(l+1)，d=n-l(r+1)-(r-1)。

证明：根据引理3可以计算出n和k，以及d≥n-(r+1)l-(r-1)h，又因为在有理函数域中h=deg(x)=[Fq(x):Fq(x)]=1，因此

d≥n-l(r+1)-(r-1)，

因为码C(D,V)的最小距离满足

计算得

d≤(r+1)s-(l+1)r-(l+1)+2

=(r+1)s-(l+1)(r+1)+2

=(r+1)(s-l-1)+2

=(r+1)s-(r+1)l-(r+1)+2

=n-l(r+1)-(r-1)

因此

d=n-l(r+1)-(r-1)

即

则码C(D,V)是Fq上距离最优的(n,k,r)LRC码。

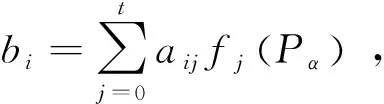
因此定义译码多项式为:

其中,deg(δ(x))≤r-1，且{x(Pβ)}Pβ∈Ai{Pα}，i={1,…,m}是互不相同的，丢失的符号可以通过Ai剩余r个位置Pβ∈Ai{Pα}对应的符号通过插值得到，一旦δ(x)确定，则丢失的符号为δ(x)(Pβ)。

例1取q=13，r=3，则x,y都是F13上的超越元且满足x4=y，则t=3，设F′=F13(x)，F=F13(y)，则F′/F13、F/F13均是F13上的有理函数域，[F′:F]=4。因为|S|≤t，所以可以取|S|=3，则S={P1,P3,P9}，P的划分A={A1,A2,A3}，其中A1={P1,1,P1,5,P1,12,P1,8}，A2={P3,2,P3,10,P3,11,P3,3}，A3={P9,4,P9,7,P9,9,P9,6}。设D=P，P是x的极点，degD=l=1，L(D)=〈1,x4〉，dim(L(D))=m=l+1=2，则函数空间V=〈fjxi,i=0,1,2,j=1,2〉={1,x,x2,x4,x5,x6}，

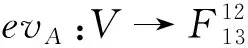
f(f(Pij),i=1,2,3,j=1,2,3,4)，

映射的像为C(D,V)，其中n=s(r+1)=12，k=rm=6，d=n-l(r+1)-(r-1)=5，所以码C是F13上距离最优的(12,6,3)LRC码。

4 结 语

本文在有理函数域上构造了距离最优的LRC，并且在F13上构造了一个距离最优的(12,6,3)LRC码。本文是在针对一个符号丢失的情况下的恢复，后续可将此构造方法扩展至多个符号丢失的情况。

最后，我要感谢我的导师胡万宝教授对我论文的指导。