带有扰动输入和时变时滞的线性中立型系统的可达集的界
陈 昊,梅学婷,康 卫
(1.淮北师范大学 数学科学学院,安徽 淮北 235000;2.阜阳师范大学 信息工程学院,安徽 阜阳 236041)
0 引言
时间延迟(时滞)存在于各种实际系统中,如生物网络、人工神经网络、物理过程、化学过程、种群模型等. 时滞可能会导致系统振荡或不稳定[1-3]. 自首次将时滞引入动态系统以来,关于时滞动力系统的研究一直受到人们的极大关注[4-5]. 另一方面,在自然现象和工程系统中,扰动在很大程度上也是不可避免的[6-8]. 因此,对于具有时滞和扰动的动力系统的研究是一个有着重要意义的课题.
线性中立型系统可以看作是时滞动态系统的一个特例,它可以在许多实际系统中遇到,如电路系统、人口动态模型、网络控制问题等[9-10]. 由于系统涉及到时滞状态的导数,所以研究线性中立型网络是一个比较复杂的问题[11-12]. 据我们所知,目前对于具有离散时滞和扰动的线性中立型系统的可达集进行研究的文献非常少,因此对其进行进一步的深入研究是非常必要的.
1 预备工作
考虑如下具有输入扰动的线性时滞中立型系统:

其中:z(t)∈Rn是状态向量,ω(t)∈Rm是扰动.τ(t) 是离散时滞,σ>0 是中立型时滞(常数).A∈ Rn×n,B∈ Rn×n,C∈ Rn×n,D∈ Rn×m,A,B,C,D是常数矩阵 .
时滞τ(t)满足条件:其中τm,τM,μ是常数,d=max{τM,σ}.
扰动ω(t)满足条件:ωT(t)ω(t)≤ω2m,其中ωm是常数.
引理1
引理2[2]对任意常数矩阵P=PT>0 及常数h2>h1>0,下式成立:

引理3[1]对任意常数矩阵R>0 及常数h2>h1>0,下式成立:

引理4[3]设f1,f2,…,fN:Rm↦R ,且在 Rm的开子集D上都是正值函数. 如果D上关于fi的倒凸集合满足条件:

引理5[13]对任意向量x1,x2,常数矩阵Ti(i=1,2,3,4),S及常数α>0,β>0,α+β=1,如果满足条件:

则下式成立:

引理6[14]设V是根据系统(1)所构造的李雅普诺夫函数,如果则V≤ 1.
2 主要结论
定理1若存在维数适当的矩阵P>0,Q1>0,Q2>0,R1>0,R2>0,K1>0,K2>0,K3>0,K4>0,S,N,单位矩阵I及常数α>0,使得如下不等式成立:

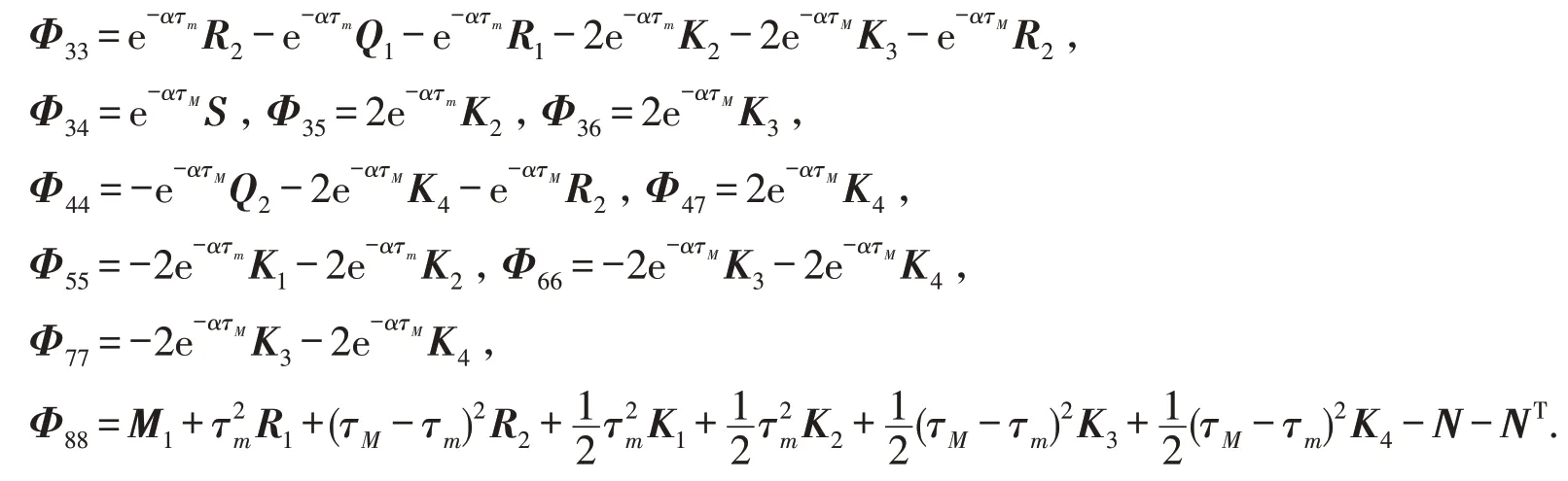
证明构造李雅普诺夫泛函其中

沿着系统(1)对V(zt)关于时间t求导,可得:


根据引理2,

根据引理3,
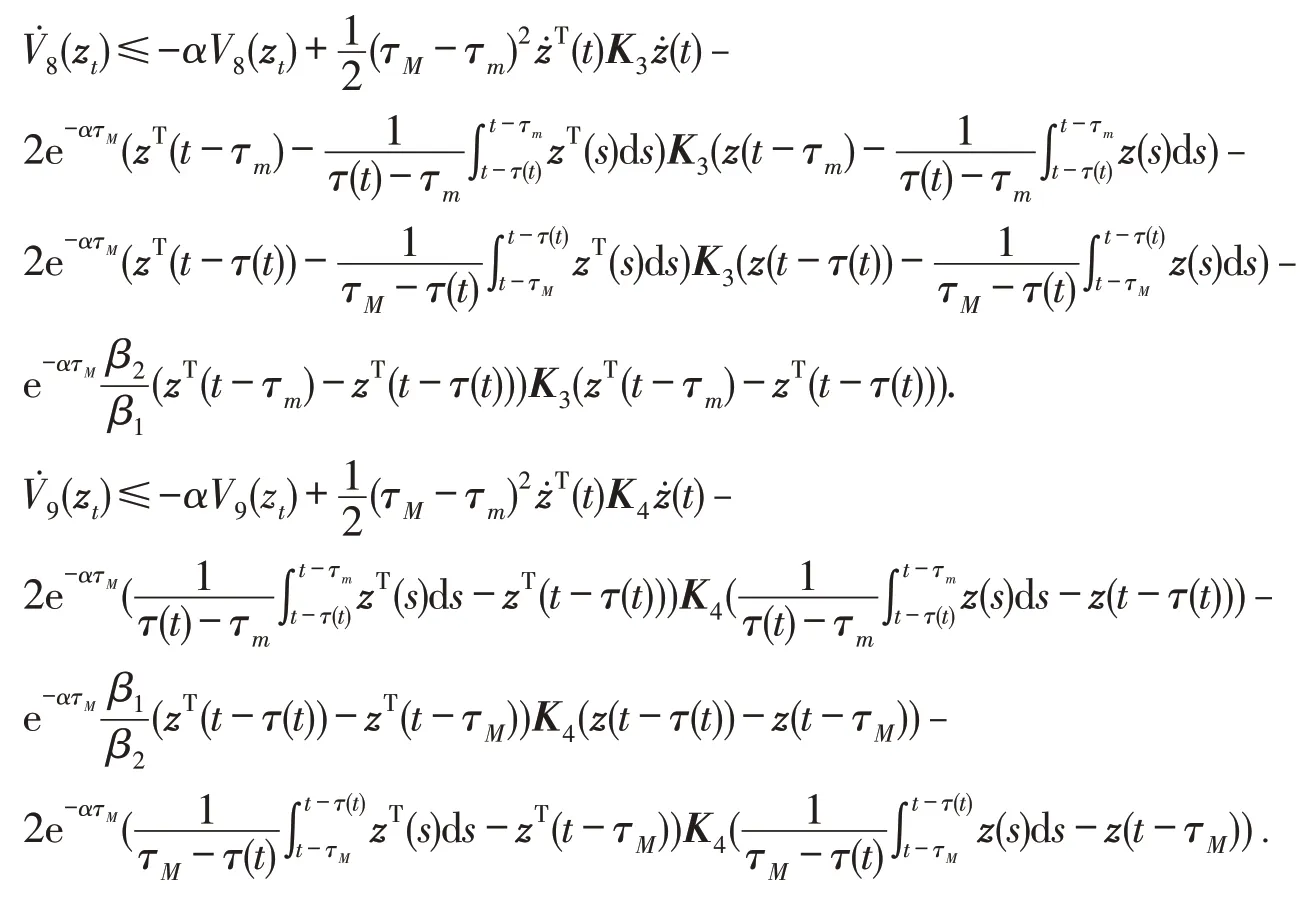
由引理5可得:

显然,下式成立:
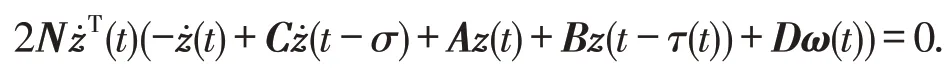
结合以上各式有:

由于式(2)(3)成立,所以下式成立:
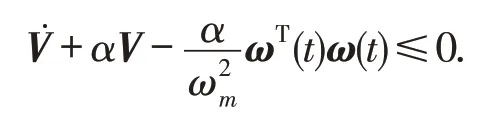
根据引理6,可得V(zt)≤1.
由对称正定矩阵谱的性质有:λmin(P)‖z(t)‖2≤V(zt),进一步可得
若在系统(1)中,C=0,0 ≤τ(t)≤τ,τ(t)≤μ,则有如下推论成立.
推论1若存在维数适当的矩阵P>0,Q>0,R>0,K1>0,K2>0,M>0,S,N,单位矩阵I及常数α>0,使得如下不等式成立:


考虑具有不确定性的线性中立型系统:

若在系统(1)中,0 ≤τ(t)≤τ,τ̇(t)≤μ,则有如下结论成立.
定理2若存在维数适当的矩阵Pi>0(i=1,2,…,N),Q>0,R>0,K1>0,K2>0,M1>0,M2>0,S,N,单位矩阵I及常数α>0,使得如下不等式成立:

注1求解系统(1)的可达集可以归结为下述最优化问题的求解(δ>0):

3 数值算例
例1考虑如下的系统:

且ωT(t)ω(t)≤1.
应用推论1,当μ=0 时,可得可达集的半径r的值如表1所示.

表1 τ 取不同值时半径r 的值
例2考虑如下的中立型系统:
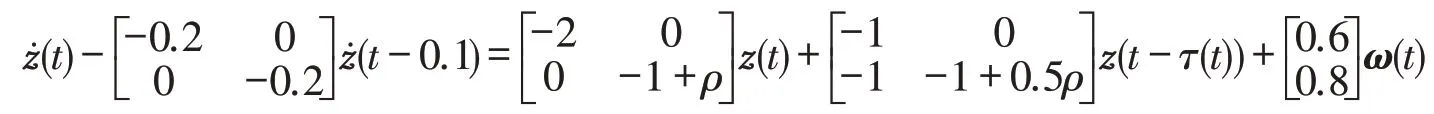
且 |ρ|≤0.2,ωT(t)ω(t)≤1.
应用定理2,可得不同情况下δ的值如表2和表3所示.

表2 δ 的值(τm=0,τM=0.7)

表3 δ 的值(τm=0,τM=0.75)
4 结语
本文研究线性中立型系统的可达集边界问题. 运用时滞分割技巧、倒凸理论、自由权矩阵及线性矩阵不等式方法,得到线性中立型系统可达集边界计算的一种方法. 从表1、表2及表3可看出,该方法较文献[13,15-18]中的计算方法所得结果更好. 可以将本文的方法推广到非线性中立型系统可达集边界的研究,有望得到更紧致的可达集新的判定条件.

