数学问题解答
2020年7月号问题解答
(解答由问题提供人给出)
2551设△ABC的面积为S,证明:
(华中师范大学国家数字化学习工程技术研究中心 彭翕成 曹洪洋 430079)
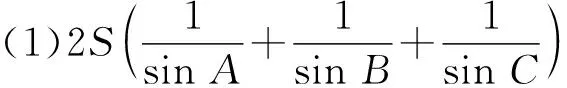
=ab+bc+ca.
(2)a2-(b-c)2=2bc(1-cosA)
则
=S.

(江苏省溧阳市光华高级中学 钱德全 213300;江苏省溧阳市永平小学 张晓蔚 213333)
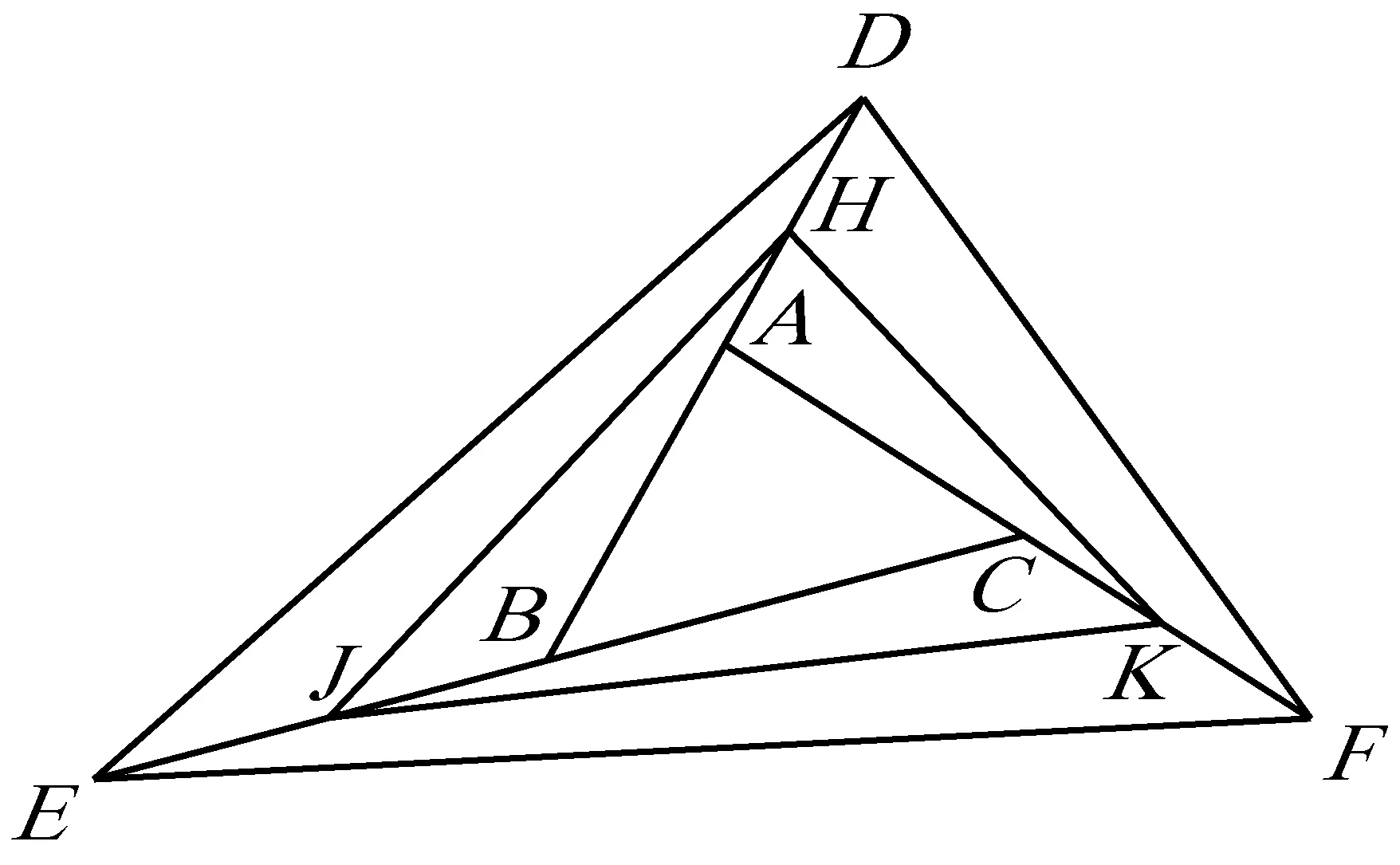
证明如图,建立平面直角坐标系,
设A(x1,y1),B(x2,y2),C(x3,y3),
△ABC的重心为M.根据三角形的重心坐标公式,



设D(xD,yD),E(xE,yE),F(xF,yF),
根据线段的定比分点坐标公式,得
所以点D((m+1)x1-mx2,(m+1)y1-my2).
同理可得
点E((m+1)x2-mx3,(m+1)y2-my3),
点F((m+1)x3-mx1,(m+1)y3-my1).
设△DEF的重心为M′(x′M,y′M),
根据三角形的重心坐标公式,得
所以△DEF的重心M′的坐标也为
所以,点M与点M′重合.
因为点H,J,K,分别是DA,EB,FC的中点,

设△HJK的重心为M″(x″M,y″M),
同理可得M″的坐标也为
所以,点M、M′、M″三点重合,命题得证.
2553在锐角△ABC,求证:
2cosAcosB+2cosBcosC+2cosCcosA
≤4cosAcosBcosC+1
≤cosA+cosB+cosC.
(安徽省枞阳县宏实中学 江保兵 246700)
证明首先证明
4cosAcosBcosC+1
≤cosA+cosB+cosC.
因为在△ABC中有三角恒等式
cosA+cosB+cosC
所以原不等式等价于



即4cosAcosBcosC+1≤cosA+cosB+cosC.
再来证明
2cosAcosB+2cosBcosC+2cosCcosA
≤4cosAcosBcosC+1.

则有1-2cosA≥0.
因为2cosAcosB+2cosAcosC+
2cosBcosC-4cosAcosBcosC-1
=2cosA(cosB+cosC)+
2cosBcosC(1-2cosA)-1
+cos (B-C)](1-2cosA)-1
所以
2cosAcosB+2cosBcosC+2cosCcosA
≤4cosAcosBcosC+1.
综上
2cosAcosB+2cosBcosC+2cosCcosA
≤4cosAcosBcosC+1
≤cosA+cosB+cosC.
(当且仅当三角形△ABC为正三角形时等号成立)
2554已知⊙O为△ABC的外接圆,⊙Ia为∠BAC内的旁切圆,∠A的外角平分线交⊙O于点P,直线PIa交⊙O于点T,⊙Ia切BC于点D,切AB的延长线于点E.求证:∠ATP=∠DTP.
(江西省高安市石脑二中 王典辉 330818)
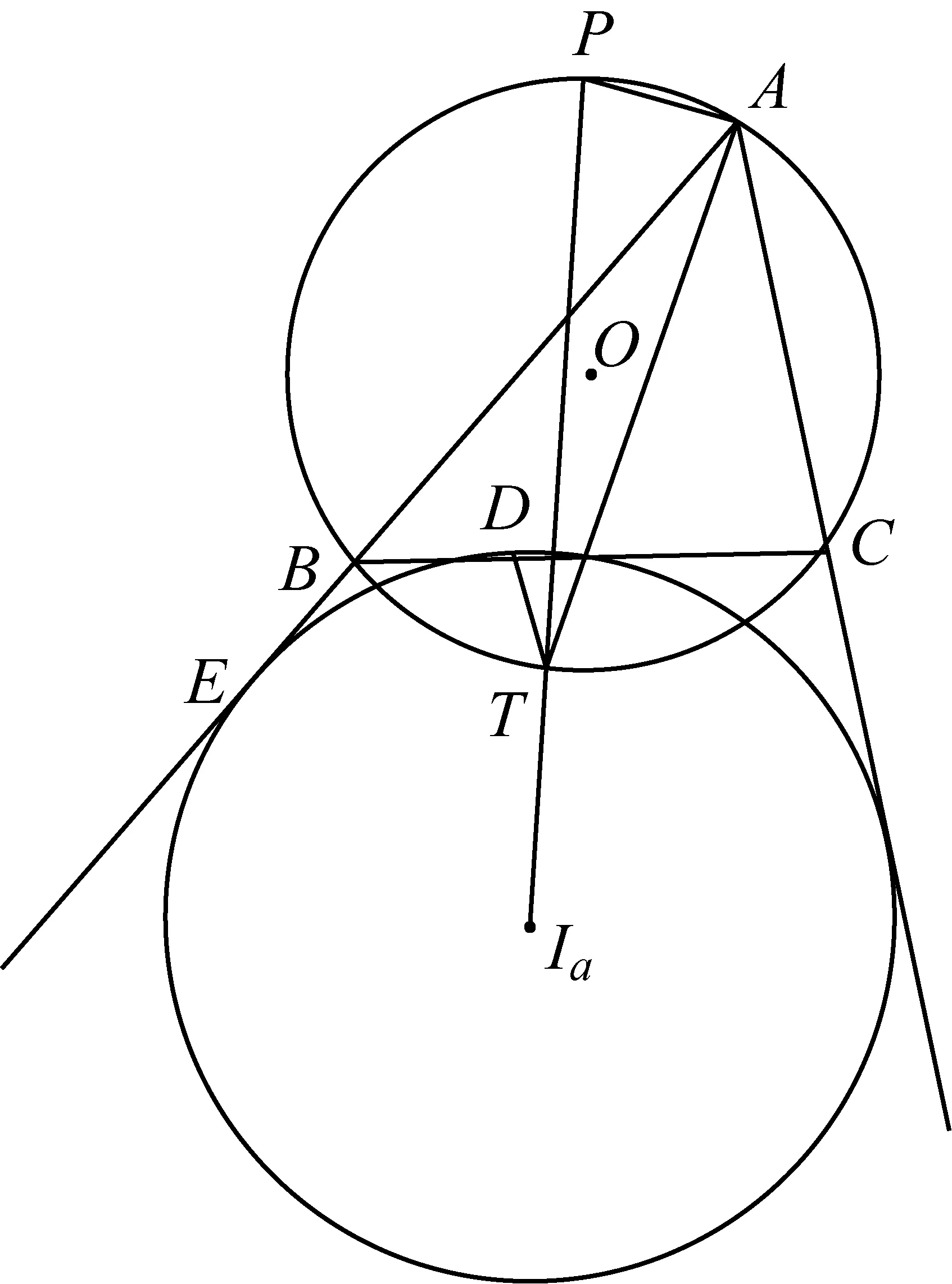

证明联接AIa交⊙O于点Q,联接PQ交BC于点K,AP是∠A的外角平分线,
可得∠PAQ=90°,可知PQ是⊙O的直径,
根据垂径定理知PQ垂直平分线段BC.
联结BQ,BIa,
因为∠EBIa=∠CBIa=∠CBQ+∠QBIa
=∠BAQ+∠BIaQ,
而∠CBQ=∠BAQ,
所以∠QBIa=∠BIaQ,得BQ=IaQ.
联结PB、KIa,根据直角三角形的射影定理,有
BQ2=QK·QP=IaQ2,
从而△PQIa∽△IaQK,
所以∠IaPQ=∠KIaQ.
联结IaD,又因为PQ⊥BC、IaD⊥BC,
所以PQ∥IaD,得∠IaPQ=∠DIaT,
所以∠KIaQ=∠DIaT,
从而有∠DIaK=∠QIaT,
联结TQ,可知有
∠PTQ=90°=∠QTIa=∠IaDK,
所以有△IaDK∽△IaTQ,

因为∠KIaQ=∠DIaT,
所以△DIaT∽△KIaQ.
易得
△DIaT∽△KIaQ∽△IaPQ∽△IaAT,
有∠IaTD=∠ATIa,
所以∠ATP=∠DTP.
2555正实数x,y,z满足xyz≥1,证明:
(兴化市教育局教研室 张 俊 225700)
证明由六元均值不等式有

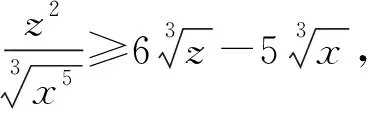

①
由十一元均值不等式及xyz≥1有

②
由①②有

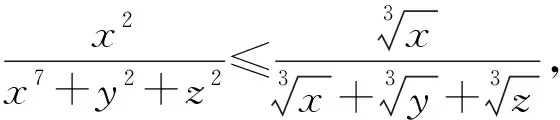

以上三式相加得
≤1.
③





以上三式相加得
≥1.
④
由③,④得
≥0.
2020年8月号问题
(来稿请注明出处——编者)
2556如图,已知Rt△MNT,∠MTN=90°,点O是MN中点,点I、J是TM、TN上的点,满足OI⊥IJ,点X是IJ中点,点Y是MN上的点,满足∠NIY=∠TMN,证明:XY⊥MN.
(安徽省滁州中学 李伟健 239000)


(河南省南阳师范学院软件学院2017级9班 李居之 孙文雪 473061)

(浙江省慈溪市慈溪实验中学 华漫天 315300)

(1)
(河南质量工程职业学院 李永利 467001)
2560⊙O的半径等于等边△ABC的高,且⊙O在BC边上滚动时与AB、AC两边交于E、F,求证:无论⊙O滚到什么位置,△OEF总是等边三角形.

(安徽省淮南三中 王秉春 232007)

