数学实验教学内部支持系统的构建①

孙朝仁

(江苏省苏州市教育科学研究院 215004)

教学支持系统就是把学习对象及其相关要素作为系统，从系统和要素、要素和要素、系统和环境的相互联系、相互作用，综合考察学习对象的一种教学方法．数学实验内部教学支持系统，主要包括概念发生系统、思维还原系统、经验重构系统，主要涉及数学内部关系维度、系统关联维度和经验增值维度．这些维度要素的相互作用与相互联系，有助于学生学深、学透、学好数学．

本文主要在“数学实验”系统思维的参与下，建构数学实验内部教学支持系统，促进数学实验教学转型和做好实验教学．

1 构建概念发生支持系统，突出“学”与“思”的交互作用

概念是数学实验的“基石”，经历概念的发生过程是学生习得概念绕不开的思维路径．任何概念的发生都需要支持条件，包括外部关系维度(实验环境的支持与互动、实验工具的选择与匹配、学习心理过程的调适与稳态等，另文已有研究，这里不再赘述)和内部关系维度．从内部关系维度来看，支持概念发生的条件包括先行组织、分布式认知策略的支持与适切、学生的“学”与“思”，及其系统思维的内部交互作用．比如，实验教学中通过引入变量，用变量之间的对应关系描述事物的变化过程，研究事物的变化规律，是“用函数模型”定量研究事物变化规律的精要所在，也是从内部支持函数概念发生的一个经典样例．具体来说，研究二次函数图像的性质，需要基于“一次函数”“反比例函数”的图像画法及其性质的获得过程作为认知支持条件，这就是从内部关系描述概念的发生过程，使得学生新旧知识自然衔接．换句话说，经历概念的发生过程，主要是经历概念的抽象过程．数学教学应让学生经历完整的抽象过程、参与完整的抽象活动——感知与识别、分类与概括、想象与构建、定义与表征、系统化与结构化．

图1

数学实验作为概念抽象的行为载体，在促进概念发生的同时，不仅可以提高学生的数学抽象水平，同时也有助于发展学生的思考能力．学与思是“做好”数学实验的精髓，是“教好”数学思考的内部支持条件．在苏霍姆林斯基看来，“要培养自己孩子的智力，那你就得教给他思考．”由此可见，思考是概念习得的关键与根本，是数学实验的本质所在，是学好数学的关键．《义务教育数学课程标准(2011年版)》明确指出，“数学思考就是让学生在参与观察、实验、猜想、证明、综合实践等数学活动中，通过“做”与“思考”积累活动经验，发展独立思考、体会数学的基本思想和基本思维方式.”为此，数学实验在概念发生维度，需要提供以下三个方面的内部支持条件，方能让学生在学与思中获得概念、在学与思的交互作用中获得概念的保持与迁移能力．一是用好先行组织，降低概念发生起点；二是采用分布式认知策略，经历概念发生的抽象过程；三是“做、学、思”互动交往与结合，促进概念的获得、保持与迁移水平．

不妨以“二次函数的图像和性质”的概念发生的教学为例，从内部关系维度说明概念发生的支持条件，突出学与思的交互作用过程，具体设问过程如下：首先，直奔主题设问．即我们学过哪些函数？我们是从哪些方面研究的？二次函数的一般形式是什么？(y=ax2+bx+c．其中，a≠0，且为a、b、c为常数)下面我们该研究什么？如何研究？从哪一种函数形式入手？(y=ax2．其中，a为常数，且a≠0)；其次，让学生观察二次函数表达式，并猜想描述它的图像有什么特征？(学生回答：关于y轴对称；y的最小值为0；从左向右，图像“先降后升”；无最大值)；再次，让学生画出函数y=x2的图像．(1)如何给自变量取值更合理？从表格数据分析来看，你能描述二次函数图像的特征吗？(因为当x=±1时，y=1，所以由点的对称，猜想该图像是关于y轴对称；随着x值的增大，y的值“先减后增”)(2)画图像时为什么要用平滑的曲线连接而不用折线连接？(除了“折点”，折线上的任一点都不在二次函数y=x2的图像上，所以不可以用“折线”连接)(3)观察图像并描述二次函数y=x2的图像性质．(图像有最低点，函数有最小值；当a>0时，图像开口向上；图像关于y轴对称)在揭示“二次函数图像的性质”的过程中，其中，“直奔主题设问”及其思考是先行组织行为，为“概念发生”铺设思维经验；从解析式的角度和观察表格数据走势的角度，分析猜想二次函数图像的性质是落实分布式认知策略的表现形式；在画出图像的过程中，借助回归观察，描述二次函数图像的性质，是“做学思”交互作用的基本方式，有助于学生在实验中获得体验，并将感性体验及时上升到理性思考的高度．这就是数学内部关系给数学实验提供的最好支持条件，实现“做中学”与“做中思”的目标．

2 构建思维还原支持系统，突出“说”与“述”的参与作用

数学实验的目的不止于帮助学生理解数学，更在于系统关联，突破知识接受的瓶颈，将不好理解转化为好理解、不能解决的转化为可解决、将“学术性”知识转化为“教育性”内容，让学生在“思维还原”中获得智慧，提高思维还原的水平．像二次函数图像为什么用平滑的曲线连接，而不用折线连接？只有让学生在研究分段函数的基础上，才能明白“曲线”与“折线”的不同．一般来说，大部分课堂都是“告诉式教学”(只强调用平滑的曲线连接，而不说为什么)，没有让学生从思维还原中感知“平滑有理、折得有误”，也就是说没有提供适切的实验教学支持条件．具体来说，思维还原的支持条件包括举例说明、概念辨别、概括反思以及类比化规等支持要素和系统要素的交往与互动.《义务教育数学课程标准(2011年版)》明确指出，“教师应该根据不同学习阶段的学生的年龄特征和认知水平、根据学段目标，合理设计并组织实施综合实践活动．”这是由学生问题解决的心理水平决定的．一般来说，数学问题解决能力的发展依赖于5个相互关联的要素，即概念、技能、过程、态度和元认知．其中，元认知也就是对认知对象的认知，是指个人对自己的思维过程的认识与反思，进行恰当的监控与调节，促进思维的有序还原．像研究二次函数图像的性质，让学生在画出图像的过程中(列表、描点和连线)，观察图像的特征，在描述图像性质的过程中，通过元认知监控(为什么要用平滑的曲线连接，而不能用折线连接等)，将5个支持要素相互关联，促进概念抽象，这就是数学实验内部支持系统构建的具体表现．

当然，从系统关联的维度看思维还原支持条件，还需要突出“说”与“述”的参与．“说”旨在让概念认识浑然天成、整体通透，“述”旨在让概念理解逻辑清晰、思维融通，在“说”与“述”的过程中强化元认知．这里的元认知是一种数学反思，是概念、技能、过程与态度的上位概念，是数学实验教学的精髓．可以说，没有元认知就没有概念系统及其要素的关联，没有元认知就没有思维还原．换句话说，元认知是思维还原的主要支持体系，是学生建立知识关联的思维桥梁，是“过程目标”转化为“目标过程”的思维路径，也是通过“说”与“述”来表现的．为此，就系统关联教学支持体系视角来说，需要做好三个方面的工作：一是通过“做”数学，让学生在实物画图中感知图像性质的来龙去脉；二是通过“说”数学，让学生在描述图像性质的过程中，形成概念产生式系统；三是通过“述”数学，让学生在复述过程中，形成稳定的概念关联系统．

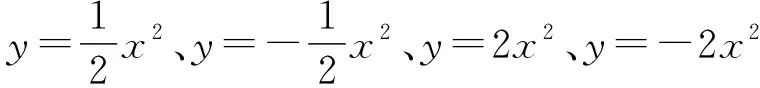
3 构建经验重构支持系统，突出“做”与“用”的补偿作用

经验增值是数学实验教育的价值追求，呈现学生“做好实验”“学好数学”的积极心理状态．按照庞加莱和阿达玛的观点，“数学创造就是辨别，就是选择．选择什么？就是选择所期待的思想组合．”这里的“辨别”“选择”与“组合”都是经验成分的重组与再造，既是经验重构的支持条件，也意味着新经验的再生，标志着经验适用范围的扩大，以及经验水平的增值．从数学实验教学支持系统构建的目的来说，数学实验不止于理解数学或数学理解，更在于数学创造和创造数学，这就是数学实验教育的现代化朝向，也是数学实验的育人价值所在和变换角度看问题的能力体现，还是数学实验的内部支持力量．像通过计算机软件探讨“二次函数图像的平移”就是对“一次函数图像的平移”的经验重构．具体来说，对于一次函数y=2x+1的图像，如果向上平移3个单位，就可以得到函数y=2x+4的图像；如果向下平移3个单位，就可以得到函数y=2x-2的图像．基于这样的“平移经验的组合”，我们可以猜想验证得到二次函数y=2x2+1的图像，如果向上平移3个单位，得到的是函数y=2x2+4的图像；如果向下平移3个单位，得到的是函数y=2x2-2的图像．这就是经验增值的具体表现．当然“经验重构”还需要“做”与“用”的补偿作用．

“经验重构”心理水平是后天学习活动的过程性结果，是长期“做数学”和“用数学”的经验缓存和补偿．其中，生物表观机制的经验成分并不普遍(表观机制是一种医学概念，即为遗传学理)，主要是对缓存经验的重组与调用．一般来说，经验调用和重构的质量是一种内在的核心素养，是提出问题的经验基础，是靠“四基”“四能”支撑的能力复合体．《上海市中小学数学课程标准(实验稿)》对数学核心素养的界定，即“人们通过数学教育以及自身的认知活动，所获得的数学基础知识、基本技能、数学思想和观念，以及由此形成的数学思想品质和解决问题的能力综合．”这就要求数学实验既要重视“四基”的不同发展，又要强化“四能”的教学支持体系的构建，不止于外部环境的创设，更在于经验的重组与调用，扩大经验的适用范围，提高经验增值水平，方能让学生在习得知识技能、思想方法的同时，获得核心素养的内生长，增长数学才干和服务社会的能力．为此，需要做好三个方面工作：一是做好数学，为经验调用就绪积极的心理状态；二是用好数学，为经验增值铺设思想基础；三是重构数学，为经验迁移和经验再造提供教学支持．

不妨以“二次函数的图像和性质”的教学反思环节为载体，以此说明经验增值之道，突出数学实验“做”与“用”的补偿作用．具体活动流程设计如下：首先，呈现本节课的知识运行线索和框架结构，在智能的“做”的参与下，引导学生回顾本节课“做”数学的经历，强调“列表、描点和连线”是研究函数图像的一般方法，同时通过元认知监控的方式(在列表、描点的基础上连线，为什么用平滑曲线，而不用折线连接)指出“抛物线是平滑曲线”的依据．其次．基于智能“用”提出问题，即这节课我们研究了函数y=ax2的图像与性质，你认为我们还需要研究二次函数哪些形式？(即y=ax2+c和y=ax2+bx，也就是需要研究顶点在y轴上和顶点在x轴上的二次函数的图像和性质，这样有助于单元概念的建立，突出经验增值的意义．)最后，基于“经验重构”和经验外扩呈现问题，即你认为我们应该怎样研究函数y=x3和y=x4的图像与性质？(这样的设计，有助于比较研究，也有助于拓展学生的思维留白空间，扩大经验适用范围)这一问题的提出，一方面可以扩大“列表、描点和连线”的适用范围，另一方面也可以拓展学生的思维空间，丰富学生的知识结构，促进纵向数学化的能力，为后续高中“幂函数”的学习铺设思维轨道，提供经验支持．

如果说，如何使学生愿意学，喜欢学，对数学感兴趣是数学实验外部支持体系决定的，那么，如何让学生做自己能做的事，并对自己所做的事负责则是由数学实验的内部支持体系决定的．因此，数学实验内部支持系统的构建，意义重大，价值不菲．