摄动-增量法解Duffing-Van der Pol方程极限环

李军桦，汪海玲，李祖雄

(1.湖北民族大学 数学与统计学院，湖北 恩施 445000;2.广西师范大学 数学与统计学院，广西 桂林 541004;3.重庆三峡学院 数学与统计学院，重庆 万州 404199)

Duffing方程是研究重力摆和端部有集中质量的弹性梁的经典例子,同时也是单摆摆动模型、金融模型等众多实际系统的简化形式[1-2].Van der Pol方程是20世纪20年代由Van der Pol在研究电子管振荡和模拟人的心脏搏动的基础上提出的一类典型的非线性方程[1].Duffing方程和Van der Pol方程都有着非常丰富的非线性动力学特性,所以得到了国内外众多专家、学者的广泛研究,常常被用做研究混沌控制和动力学行为的试金石.而Duffing-Van der Pol方程则是上述两者的组合形式,其非线性部分同时含有Duffing方程的三次非线性恢复力项和Vander Pol方程维持自激振动的非线性阻尼项,这种特殊的形式使得对此方程更具有可研究性,因而也成为学者们研究非线性动力学和混沌的主要模型.

Duffing-Van der Pol系统是强非线性系统中一类具有代表性的系统,而且被广泛应用于科学、生物、工程等领域;同时也常被用来模拟色散媒介(折射率依赖于光学强度)中的光学的稳定性[3],也常用于模拟流量导致的结构的振动问题[4];这也有益于直接理解非线性振动中的动态行为,很多学者对Duffing-Van der Pol方程进行了深入研究,文献[5]研究了不带外力的Duffing-Van der Pol方程的随机形式,而分支结构、混沌和混沌控制在文献[6-8]中进行了研究,在文献[9]中用随机平均法研究高斯白噪声激励下分数阶Duffing-Van der Pol方程的稳定响应.

在微分方程的理论和应用中,极限环已被广泛应用于医学、生物学的定性分析[10-11],而对于如何计算极限环的个数及其分布都缺乏比较有效的计算方法.本文将应用一种求解Duffing-Van der Pol方程极限环解析解的定量方法—摄动-增量法[12].摄动-增量法是在1996年Chan等在摄动-迭代法[13]的基础上进行改进并提出的一种求解强非线性振动的新方法.该方法把摄动法和增量法相结合起来,将参数λ的取值范围进一步扩展.近年来,摄动增量法被广泛应用于非线性动力系统中的极限环、同(异)宿轨、同(异)宿分岔的计算[14-20]中,摄动增量法还可被用于研究不连续振动系统的解析解及脉冲系统分支[21]、耦合非线性振动系统[22]和二自由度气动弹性系统的极限环振动系统[23-24].

1 系统模型

Duffing方程可以表示为：

(1)

其中α称为阻尼系数,c1和c3分别称为线性和非线性刚性系数.

Van der Pol方程可以表示为：

(2)

Duffing-Van der Pol方程的非线性部分同时含有Duffing方程的三次非线性恢复力项和Van der Pol方程维持自激振动的非线性阻尼项,其方程形式为：

(3)

其中c1和c3分别称为线性和非线性刚性系数,非线性项λ(x2-1)表示非线性阻尼.

2 摄动-增量法

考虑一般的强非线性系统：

(4)

对方程(4)作非线性时间变换：

(5)

其中φ是新时间,由参考文献[25]知在φ域内极限环的近似解可以表示为：

(6)

其中a是振幅,b是偏心.把方程(4)变换成φ的时间域,有：

(7)

(8)

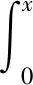
为简便起见,记：

(9)

(10)

在式(8)中分别令φ=π和2π,得:

(11)

(12)

若由式(8)、(11)、(12),可以求得a、b和Φ(φ),则极限环表达式可以得到.如果:

(13)

b=0,Φ(φ+π)=Φ(φ).

(14)

摄动-增量法的具体求解过程分为两步：

第一步为摄动法.当λ≈0时,这时a、b和Φ(φ)可以表示为:

a=a0+O(λ),b=b0+O(λ),Φ=Φ0+O(λ).

(15)

代入式(8)、(11)、(12),得:

(16)

V(-a0+b0)-V(a0+b0)=0,

(17)

(18)

由式(16)、(17)、(18)解出a0、b0和Φ0(φ)后,可得极限环的零阶近似解.

第二步为参数增量法.它将把对应于小参数的解延拓至大参数.设a0,b0和Φ0对应于参数λ0的解(即开始时λ0≈0,对应于零阶近似解).现在给λ0一个小增量Δλ(0<Δλ≪1),λ=λ0+Δλ对应的解记为：

a=a0+Δa,b=b0+Δb,Φ=Φ0+ΔΦ.

(19)

将式(19)代入(8)、(11)、(12)中,得到增量方程:

(20)

(21)

(22)

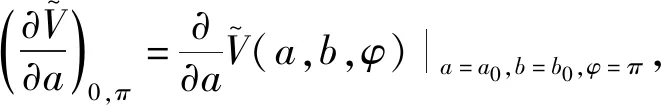
由于Φ(φ)是2π周期函数,故可以展开为Fourier级数：

设取M个谐波项,只要M充分大,Φ(φ)就有足够的精度,同样,ΔΦ(φ)也可展开为Fourier级数：

将增量方程(20)～(22)中的周期函数都展开为Fourier级数:

把上述增量展开式代入方程(20)～(22),然后令方程两边的常数项cosjφ和sinjφ项的系数分别相等,即应用谐波平衡法,可得Δa、Δb、ΔP0、ΔPj和ΔQj的线性方程组:

(23)

其中n=0,1,…,2M+2,R0为式(20)右边的常数项,Ri和RM+i分别为式(20)右边Fourier级数展开式中余弦项和正弦项的系数,R2M+1和R2M+2分别为式(21)和式(22)右边的值.因此,如果所有Rn趋于零,则a0、b0和Φ0(φ)就是式(8)、(11)、(12)的解.求解线性代数方程组(23)得Δa、Δb、ΔP0、ΔPj和ΔQj后,再代入式(19)得a、b和Φ(φ)并作为新的a0、b0和Φ0(φ).重复上述迭代求解过程,当所有Rn小于预先规定的误差时,迭代结束.此时得到对应于λ=Δλ的解a、b和Φ(φ)满足给定误差的极限环及对应变换的近似表达式(6).再以此时的值作为新的初值,又给参数以增量Δλ,重复上述迭代过程,经过N次增量后λ=NΔλ,当N足够大,就得到了大参数的对应的解.

3 解Duffing-Van der Pol方程极限环

考虑如下一类Duffing-Van der Pol 方程:

(24)

本文令c0=1,c1=0,c2=1,c3=1.此时原方程变为:

(25)

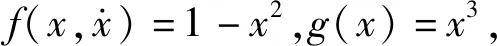
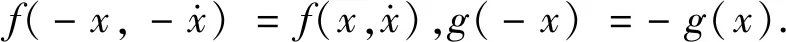
(26)

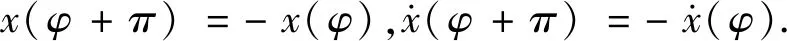
(27)

由方程(6)可知:

b=0,Φ(φ+π)=Φ(φ).

(28)

因此有:

(29)

方程(23)改写成:

(30)

根据方程(9)、(10)和(16),可知:

(31)

(32)

(33)

3.1 零阶摄动解

由方程(18)求得零阶摄动解为:

(34)

下面给出λ≈0时的二维流线图(如图1所示)和极限环相图(如图2所示).

图1 λ≈0时方程(25)的二维流线图 图2 λ≈0时的极限环相图Fig.1 λ≈0,two dimensional streamline diagram of equation (25) Fig.2 λ≈0,the phase diagram of the limit cycle

3.2 参数增量法

取λ0=0,令Δλ=0.01,M=4和N=10即由零阶近似解(34)经过10次增量后λ=0.1.此时方程(25)的二维流线图(如图3所示)和极限环的相图(如图4所示),图中还给出用数值积分法得到的数值解,由此可见摄动-增量法与数值积分法结果吻合.

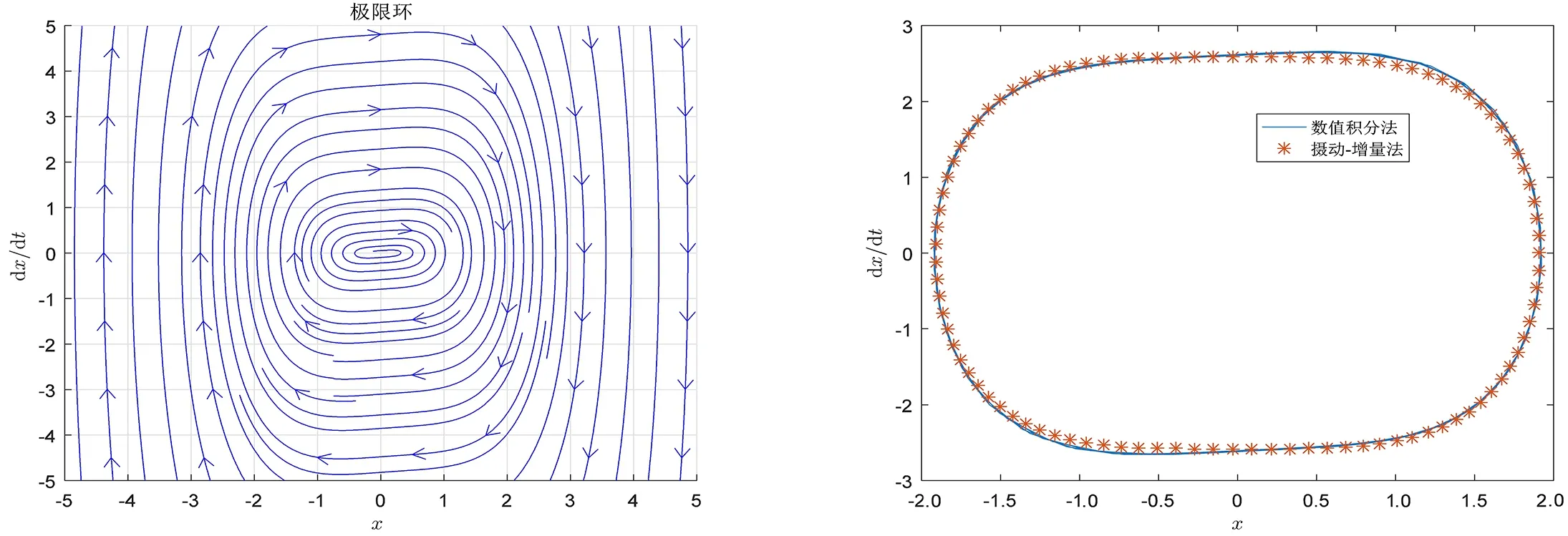
图3 λ≈0.1时方程(25)的二维流线图 图4 λ≈0.1时的极限环相图Fig.3 λ≈0.1,two dimensional streamline diagram of equation (25) Fig.4 λ≈0.1,the phase diagram of the limit cycle

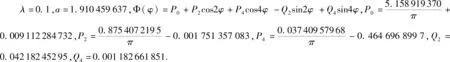
4 结论

本文为求解Duffing-Van der Pol方程的极限环提供了一种较为可行的定量方法,并且可以得到较好的结果.摄动-增量法是解析法和数值法相结合的一种新方法,利用摄动-增量法计算极限环时,不必事先知道极限环的稳定性,即不但可以计算稳定的或不稳定的极限环,而且可以计算半稳定的极限环.摄动-增量法还适用于某些含参数的系统,同时也常常用来研究极限环的稳定性和分岔等问题.如果进一步考虑多参数对系统的影响时,我们将会研究系统的分岔问题,这将会是我们下一步的工作.