相关于遗传挠理论的Rickart模

李煜彦，王奇临

(陇南师范高等专科学校 数信学院,甘肃 陇南 742500)

近年来,Rickart环和模受到了许多学者的关注[1-3].而Rickart环和模与Baer环和模[4-6]有着非常紧密的联系.Ebrahimi等[7]利用第二奇异子模引入了t-Rickart模的概念,研究了t-Rickart模的性质及等价刻画,讨论了t-Rickart模,t-Baer模和t-extending模之间的紧密关系.Asgari等[8]引入了对偶t-Rickart模,研究了对偶t-Rickart模的性质和等价刻画.Ungor等[9]从奇异子模和对偶Goldie挠理论的角度研究了Rickart模.Abdelwhab等[10]研究了其自同态环是Rickart环的模,并称其为R-endoRickart模.Çeken等[11]从遗传挠理论的角度引入τ-本质子模和τ-extending模的概念,研究了τ-extending模的直和分解.李庆等[12-13]先后研究了交换环的w-弱finitistic维数以及UP整环上的u-有限表现型模.

受上述启发,本文从遗传挠理论的角度研究了Rickart模,提出了τ-Rickart模的概念,它是t-Rickart模的推广.文中研究了τ-Rickart模的性质,讨论了τ-Rickart模与Rickart模以及τ-Baer之间的关系,给出了τ-Rickart的等价刻画.

本文中的挠理论均指遗传挠理论,环都是有单位元的结合环,模指酉右R-模.用τ(M)表示M的所有τ-挠子模的和.称挠理论是稳定的,如果挠类T关于内射包封闭,等价地说,τ(M)是M的闭子模.设S=End(MR),I≤SS用rM(I)={m∈M|Im=0}表示I在M中的右零化子,τM(I)={m∈M|Im∈τ(M)}表示I在M中的τ-零化子.

1 定义及引理

定义1[11]设N≤M,称N是M的τ-本质子模,如果对M的任意子模K,若N∩K⊆τ(M),则K⊆τ(M),记为N◁τM.此时也称M是N的τ-本质扩张.如果N没有真的τ-本质扩张,则称N是M的τ-闭子模.

引理1 设N≤M,考虑以下条件:

i)N◁τM;

iii)N+τ(M)≤eM.

则i) ⟺ii) ⟹iii).

特别地,若τ是稳定的挠理论,则ii)⟺iii).

证明i)⟺ii)由文献[14]得证.

ii)⟹iii) 由文献[15]得证.

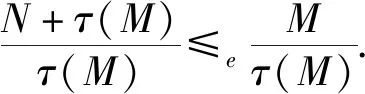
对任意f∈End(M),令τM(f)={m∈M|fM∈τ(M)}.

下面给出τ-Baer模和τ-Rickart模的定义.

定义2 称M是τ-Baer模,如果对End(M)的任意左理想I,τM(I)是M的直和因子.

定义3 称M是τ-Rickart模,如果对任意f∈End(M),τM(f)是M的直和因子.

显然,τ-Baer模是τ-Rickart模.

由定义3及文献[7]和文献[11]的内容,易得如下结论.

引理2 以下结论成立:

i) 所有半单模和τ-挠模都是τ-Rickart模;

ii)τ-Rickart模是t-Rickart模;

iii) 若M是τ-挠自由的,则M是τ-Rickart模当且仅当M是Rickart模;

iv) 若M是τ-挠自由且非奇异的,则M是t-Rickart模当且仅当M是τ-Rickart模当且仅当M是Rickart模.

证明i) 若M是半单模,则M的任意子模都是M的直和因子,故M是τ-Rickart模.若M是τ-挠模,则τ(M)=M.于是对任意f∈End(M),τM(f)=M.从而τM(f)是M的直和因子.因此M是τ-Rickart模.

ii) 由于M的Goldie挠子模τG(M)恰是M的第二奇异子模Z2(M),故τ-Rickart模是t-Rickart模.

iii) 若M是τ-挠自由的,则τ(M)=0.于是对任意f∈End(M),τM(f)=rM(f).因此τM(f)是M的直和因子当且仅当rM(f)是M的直和因子.从而M是τ-Rickart模当且仅当M是Rickart模.

iv) 若M是τ-挠自由且非奇异的,则Z2(M)=τ(M)=0.与iii)的证明类似,M是t-Rickart模当且仅当M是τ-Rickart模当且仅当M是Rickart模.

2 主要结论

下面给出τ-Baer模的等价刻画.

定理1 以下条件等价:

i)M是τ-Baer模;

ii)M=τ(M)⊕M′,其中M′是(挠自由)Baer模.

ii)⟹i) 设M=τ(M)⊕M′,其中M′是(挠自由)Baer模.令S′=End(M′),I≤End(M)End(M),A′={πM′φ|M′|φ∈I},J=S′A′,则τM(I)=τ(M)⊕rM′(J).由于M′是Baer模,故rM′(J)是M′的直和因子,从而τM(I)是M的直和因子.因此M是τ-Baer模.

由文献[1]和文献[7]知,Rickart模和t-Rickart模关于直和因子是封闭的.类似地,关于τ-Rickart模,有：

性质1τ-Rickart模的直和因子仍是τ-Rickart模.

证明设M是τ-Rickart模,N是M的直和因子,f∈End(N).设L≤M,M=N⊕L.则f⊕1End(L)∈End(M),故τM(f⊕1End(L))是M的直和因子.由于τM(f⊕1End(L))=τN(f)⊕τ(L),故由模律可知τN(f)是N的直和因子.从而N是τ-Rickart模.

下面给出τ-Rickart模的等价刻画.

定理2 下列条件等价:

i)M是τ-Rickart模;

ii)M=τ(M)⊕M′,其中M′是(挠自由)Rickart模;

iii) 对任意f∈End(M),f-1(τ(M))是M的直和因子.

证明i)⟹ii) 设M是τ-Rickart模.由于τM(1End(M))=τ(M),故τM(1End(M))=τ(M)是M的直和因子.因此存在M′≤M,使得M=τ(M)⊕M′.由性质1知,M′是τ-Rickart模.因为M′是挠自由的,所以M′是Rickart模.

ii) ⟹i) 设M=τ(M)⊕M′,其中M′是Rickart模.由于M′是M的直和因子,故存在e2=e∈End(M),使得M′=eM.

设f∈End(M),下证τM(f)=τ(M)⊕rM′(efe).

一方面,设m=m1+m2∈τM(f),其中m1∈τ(M),m2∈M′.则f(m)=f(m1)+f(m2)∈τ(M).由于f(m1)∈τ(M),故f(m2)=f(m)-f(m1)∈τ(M).于是efe(m2)=ef(m2)=0,因此m2∈rM(efe).从而τM(f)⊆τ(M)⊕rM′(efe).

另一方面,设m=m1+m2∈τ(M)⊕rM′(efe),其中m1∈τ(M),m2∈M′.因为M′=eM,所以ef(m1)=0.故ef(m)=ef(m1)+ef(m2)=ef(m1)+efe(m2)=0.因此f(m)∈Ker(e)=f(M).从而τ(M)⊕rM′(efe)⊆τM(f).

因为M′是Rickart模,所以rM′(efe)是M′的直和因子.因此τM(f)是M的直和因子.从而M是τ-Rickart模.

i) ⟺iii) 因为τM(f)=f-1(τ(M)),所以对任意f∈End(M),τM(f)是M的直和因子当且仅当f-1(τ(M))是M的直和因子,因此结论成立.

下面例子说明τ-Rickart模不一定是τ-Baer模.

例1 设R是环,M,N是R-模.若M是挠自由Rickart模但不是Baer模.则由定理1和定理2知,M⊕τ(N)是τ-Rickart模,但不是τ-Baer模.

下面利用模的SSIP性质和τ-Rickart模,给出τ-Baer模的一个等价刻画.

性质2M是τ-Baer模当且仅当M是τ-Rickart模,且M对包含τ(M)的直和因子有SSIP性质.

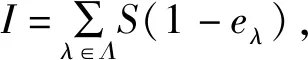
充分性 若M是τ-Rickart模,且M的包含τ(M)的直和因子有SSIP性质.由定理2知,对任意f∈End(M),f-1(τ(M))是M的直和因子.

另外,设I≤SS,则τM(I)=∩φ∈Sφ-1(τ(I)).因为τ(M)⊆φ-1(τ(M)),所以τM(I)是M的直和因子.从而M是τ-Baer模.

从而由定理1知,M是τ-Baer模.

对于自同态环没有无限非零正交幂等元的模,下面结论将说明,其模的τ-Baer性质和τ-Rickart性质是等价的.

性质3 设M是模.若End(M)没有无限非零正交幂等元,则M是τ-Baer模当且仅当M是τ-Rickart模.

证明必要性是显然的，下面证明充分性.

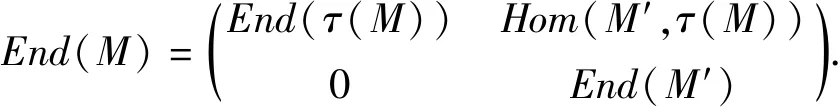
因为End(M)没有无限非零正交幂等元,所以End(M′)没有无限非零正交幂等元.由文献[1]知,M′是Baer模.从而由引理1知,M是τ-Baer模.

下面给出τ-Rickart模和Rickart模之间的一个关系.

性质4M是Rickart模且τ(M)是M的直和因子当且仅当M是τ-Rickart模,且对任意f∈End(M),rM(f)是τM(f)的直和因子.

证明必要性 设M是Rickart模,则对任意f∈End(M),rM(f)是M的直和因子,设M=rM(f)⊕H.因为τ(M)是M的直和因子,故存在N≤M,使得M=τ(M)⊕N.由文献[1]知,N也是Rickart模.于是由定理2知,M是τ-Rickart模.又因为rM(f)≤τM(f),所以τM(f)=τM(f)∩(rM(f)⊕H)=rM(f)⊕(τM(f)∩H),因此rM(f)是τM(f)的直和因子.

充分性 设M是τ-Rickart模,且对任意f∈End(M),rM(f)是τM(f)的直和因子.由定义3及定理2知,τM(f)和τ(M)都是M的直和因子.故rM(f)是M的直和因子.从而M是Rickart模.

性质5 设M是模.考虑以下条件:

i)M是τ-Rickart模;

ii) 对任意f∈End(M),存在M的直和因子K,使得τM(f)≤tesK;

iii) 对任意f∈End(M),存在M的直和因子K,使得τM(f)≤eK.

则i)⟹ii)⟹iii).

证明i)⟹ii) 设M是τ-Rickart模,则对任意f∈End(M),τM(f)是M的直和因子.令K=τM(f),则τM(f)≤tesK.

ii)⟹iii) 假设对任意f∈End(M),存在M的直和因子K,使得τM(f)≤tesK.因为τ(M)⊆τM(f),所以由引理1知,τM(f)≤eK.