基于PCA- BP 神经网络的郑州市年用水量预测

张璇

（华北水利水电大学信息工程学院，河南 郑州450046）

水资源是各个国家和地区的重要资源。近年来，我国水资源严重匮乏，各地区水资源供需不平衡，特别是在促进工业化和城市化的发展过程中，水资源利用不科学、城市水资源供需矛盾等问题日趋严重，供水水源日趋紧张。如何科学的对水资源进行规划、调度、管理、配置和决策是一个城市发展的基本问题。城市的用水量预测是根据城市过去的用水量数据及其影响因素来预测未来的需水量。城市用水量预测是水资源规划与管理的前提和基础，其预测结果直接影响给水系统调度决策的可靠性和实用性及城市水资源的可持续利用和社会经济的可持续发展[2]。目前，主要预测方法有用水定额法、指数平滑法、系统动力学、Volterra 滤波器预测法、时间序列预测方法、自回归移动、支持向量机、回归分析法[10-11]、神经网络法[1-3]、灰色预测法[4-5]以及组合预测法等[6-10]。本文主要先通过运用灰色关联法分析郑州市用水量的影响因素，并运用主成分分析法对数据进行处理后作为BP 神经网络预测模型的输入，从而建立了PCA-BP 神经网络预测模型对郑州市用水量进行预测。

1 PCA-BP 神经网络模型构建

PCA-BP 神经网络模型是将主成分分析法与BP 神经网络进行结合的预测模型，通过主成分分析法对输入因子进行处理后，再以BP 神经网络作为预测模型而构建的组合模型。该模型首先利用主成分分析法对用水量影响因素进行处理，转化为几个可以替代的主成分，然后将选取的主成分作为BP 神经网络输入特征值对郑州市年用水量进行预测。

1.1 主成分分析原理

主成分分析是把多个指标化为少数几个综合指标的一种统计分析方法。在多指标(变量)的研究中，往往由于变量个数太多，且彼此之间存在着一定的相关性，因而使得所观测的数据在一定程度上有信息的重叠。当变量较多时，在高维空间中研究样本的分布规律就更麻烦。主成分分析采取一种降维的方法，找出几个综合因子来代表原来众多的变量，使这些综合因子尽可能地反映原来变量的信息量，而且彼此之间互不相关，从而达到简化的目的。

在利用神经网络模型进行预测时，模型输入变量的筛选和输入结构的简化是影响预测效果和决定成果可靠性的重要技术。主成分分析通过数学变换将用水量原始影响因素转换成几个能够解释主要信息的“新因素”，即主成分，通过降维提高建模速度，同时这些“新因素”间彼此独立，因此可提高预测结果的准确性。

设观测样本的矩阵为

n 为样本数，p 为变量数。为使该样本集在降维中所引起的平方误差最小，必须进行两方面的工作：一是进行坐标变换，即用雅可比方法求解正交变换矩阵；二是选取m（m＜p）个主成分。

（1）将原始数据进行标准化处理，即对样本集中元素xik作

主成分分析的明显特征是每个主分量依赖于测量初始变量所用的尺度，当尺度改变时，会得到不同的特征值λ。克服这个困难的方法是对初始变量进行以上标准化处理，使其方差为1。

（2）计算样本矩阵的相关系数矩阵

（3）对应于相关系数矩阵R，用雅可比方法求特征方程|R-λi|=0 的p 个非负特征值，λ1>λ2>…叟λp叟0 对应于特征值的相应特征向量为C（i）=（C1（i），C2（i），…，Cp（i）），i=1，2，…，p，并且满足

（4）选择m（m

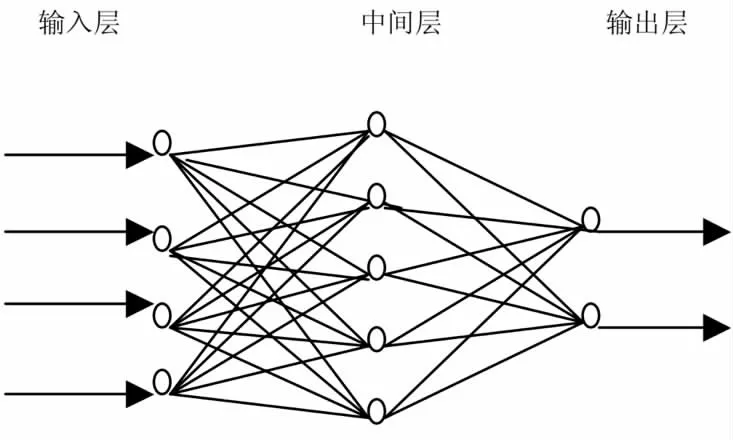
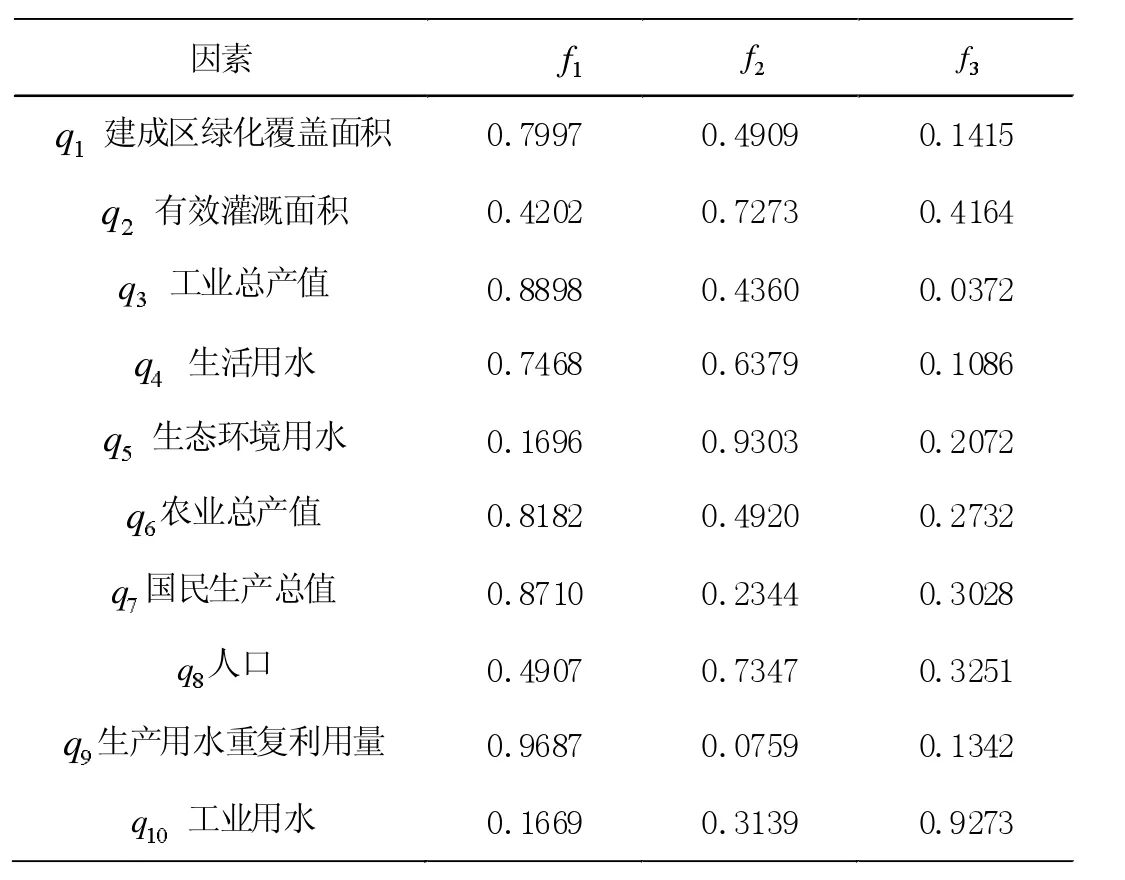
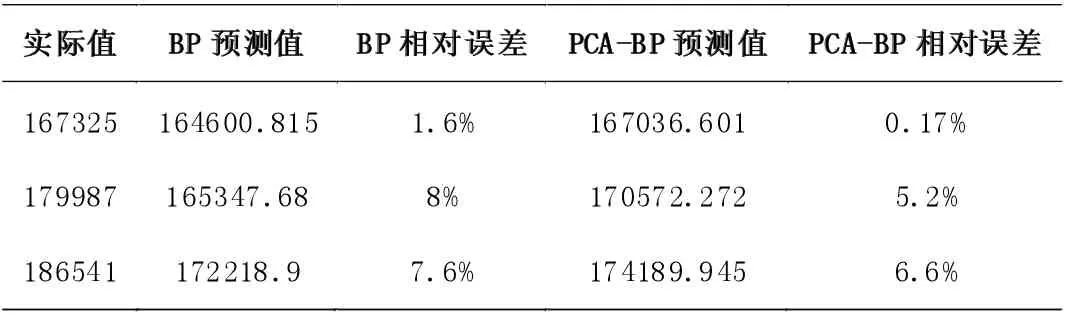
1.2 BP 神经网络原理

BP 神经网络是在1985 年Rumelhart 等人提出来的，又叫做误差反向传递学习算法，实现了Minsky 的多层网络设想，如图1 所示。

图1 BP 神经网络结构图

BP 神经网络算法包含输入层节点、输出层节点，还可有1个或多个隐含层节点。对于输入信号，要先向前传播到隐含层节点，经作用函数后，再把隐节点的输出信号传播到输出节点，最后给出输出结果。节点的作用的激励函数通常选取S 型函数，如

式中Q 为调整激励函数形式的Sigmoid 参数。该算法的学习过程由正向传播和反向传播组成。在正向传播过程中，输入信息从输入层经隐含层逐层处理，并传向输出层。每一层神经元的状态只影响下一层神经元的状态。如果输出层得不到期望的输出，则转入反向传播，将误差信号沿原来的连接通道返回，通过修改各层神经元的权值，使得误差信号最小。

设含有n 个节点的任意网络，各节点之特性为Sigmoid 型。为简便起见，指定网络只有一个输出y，任一节点i 的输出为Oi，并设有N 个样本（xk，yk）（k＝1，2，…，N），对某一输入xk，网络输

如果有M层，而第M层 仅含输出节点，第一层为输入节点，则BP 算法为：

第一步，选取初始权重W。

第二步，重复下述过程直至收敛：

（1）对于k=1 到N

a.计算Oik，netjk和y赞k 的值（正向过程）；

b.对各层从M到2 反向计算（反向过程）；

（2）对同一节点j∈M，由式（1）和式（2）计算δjk；

由此可以看出，BP 神经网络算法是把一组样本的I/O 问题变为一个非线性优化问题它使用的是优化中最普通的梯度下降法。如果把神经网络的看成输入到输出的映射，则这个映射是一个高度非线性映射。

一般来说，结构模型是根据所研究领域及要解决的问题确定的。通过对所研究问题的大量历史资料数据的分析及目前的神经网络理论发展水平，建立合适的模型，并针对所选的模型采用相应的学习算法，在网络学习过程中，不断地调整网络参数，直到输出结果满足要求。

2 评价模型建立

本文采用的评价指标是均方根误差（RMSE），相对误差，平均绝对百分误差（MAPE），模型有效度来评价模型的可靠性。其计算公式如式（3），式（4），式（5），式（6）

其中，yi表示实际值，y赞i 表示预测值，n 表示预测个数，Ei表示相对误差。

3 基于PCA-BP 神经网络的郑州市年用水量预测模型

3.1 灰色关联分析

MAE 为平均绝对误差，PMAE为平均绝对误差与装机容量的比值，实际应用中通常采用百分数的形式。

城市用水一般包括农业用水、工业用水、生活用水和生态环境用水等。农业用水主要包括农业灌溉用水和林牧副渔用水；工业用水主要指的是工业生产中的用水；生活用水包括城镇生活用水、农村生活用水、城镇公共用水、其他服务业用水等；生态环境用水指的是修复环境的用水量以及公共绿地用水量。每一个城市的用水量在一定程度上受各种因素的影响，除了会受到各方面用水量影响之外，还会受到比如气候、人口、降雨量等，本文主要通过四个方面分析了各种影响用水量因素，并选取了15 个指标与郑州市年用水量进行了灰色关联分析。

表1 年用水量和其影响因子的关联序

（1）农业方面选取的影响因素有：X1 农业播种面积，X2 有效灌溉面积，X3 农业总产值，X4 农业年用水量。

（2）工业方面对于郑州市用水量的影响选取的因包括X5 工业总产值和X6 工业年用水量。

（3）生活方面选取的因素包括：X7 郑州市人口总数，X8 人均用水量，X9 年降雨量，X10 生活用水量，X11 生产用水重复利用率，X12 建成区绿化覆盖面积，X13 生态环境用水量。

表2 各影响因素归一化后处理结果

表3 主成分的特征值、贡献率与累计贡献率

（4）经济方面包括X14 国民生产总值和X15 万元GDP 用水量。

将郑州市2002-2017 年各指标数据作为原始数据，数据来源于郑州市水利局《水资源公报》及郑州市统计年鉴。通过对数据进行标准化处理后，利用灰色关联分析对各影响因素及其总用水量之间的关联度进行计算，由表1 的计算结果，可以将影响因素大致分为两个等级：第1 级相似程度最高，包括了10 个因素，相似程度由大到小依次是：X12 建成区绿化覆盖面积，X2 有效灌溉面积，X5 工业总产值，X10 生活用水量，X13 生态环境，X3 农业总产值，X14 国民生产总值，X7 郑州市人口总数，X11生产用水重复利用量，X6 工业用水量，其灰色关联度超过了0.8，为主要影响因素；第2 级包括X9 年降雨量，X15 万元GDP用水量，X1 农作物播种面积，X4 农业用水量，X8 人均用水量，灰色关联度在0.8 以下，为次要影响因素。

因此选取作为主要影响因素Qi的10 个数据，作为后续计算的基础数据。

3.2 PCA 用水量预测输入因子确定

由于郑州市用水量受众多因素影响而增加了预测过程的复杂度，同时各因素之间的独立性有可能会对预测结果的准确性产生影响。

因此，需要对影响因素Qi进行处理和简化后，再作为预测模型的输入值。

由于各影响因素数据之间的分布及量纲差异较大，因此需要要先将数据进行归一化处理后，再进行主成分分析。本文采用的是min-max 标准化，其公式为

其中qi表示归一化后的变量，Qi表示主要影响因素的原始数据，Qimin表示第i 个影响因素的最小值，Qimax表示第i 个影响因素的最大值。归一化后的结果如表2。

利用相关软件对归一化后的影响因素qi进行主成分分析，得到主成分的特征值、贡献率与累计贡献率，如表3。由表可知前5 个主成分f1，f2，f3的贡献率分别为75.3753%，12.5250%，6.1311%，即前3 个主成分分别可解释郑州市用水量影响因素的75.3753%，12.5250%，6.1311%，且这3 个主成分的累计贡献率为94.03%，能够代表用水量主要影响因素的大部分信息，满足主成分选取的原则。

主成分中的因子载荷系数反映各因子与主成分的相关性，由表4 的因子载荷矩阵可知，主成分f1中，q1建成区绿化覆盖面积，q3工业总产值，q4生活用水，q6农业总产值，q7国民生产总值，q9生产用水重复利用量的因子载荷系数较大，因此第一主成分主要反映了q1，q3，q4，q6，q7，q9这些因素；主成分f2中，q2有效灌溉面积，q5生态环境用水，q8人口的因子载荷系数较大，因此第二主成分主要反映了有效灌溉面积，生态环境用水，人口总数这些因素；主成分f3中，q10工业用水的因子载荷系数最大，因此第三主成分主要反映了工业用水量这个因素。

表4 因子载荷矩阵

这三个主成分从不同角度反映了郑州市用水量的影响因素，因此选取这3 个主成分代替影响因素Qi作为BP 神经网络预测模型的输入值。

3.3 PCA-BP 神经网络模型预测结果及分析

以主成分分析得到的前三个因子作为输入层数据，输入节点数为3，以郑州市年用水量作为预测对象，输入节点数为1。将2002-2017 年郑州市用水量数据分为训练集和验证集，2002-2014 年数据作为训练集，2015-2017 年数据作为验证集，建立BP 神经网络预测模型，对郑州市用水量进行预测，检验PCA-BP 神经网络模型的预测效果。

另外，为了验证PCA 从简化预测模型输入因子方面提高了预测精度，本文还建立了基于相同误差水平的未用主成分分析的BP 神经网络预测模型，并将两者结果进行了对比，如表5，表6。

从表5 中可以看出在相对误差指标中，PCA-BP 神经网络模型预测的相对误差每一个都小于BP 神经网络的相对误差。从表6 中可以看出，PCA-BP 神经网络模型的RMSE，MAPE 也都小于BP 神经网络模型的评价指标，在模型有效度上，BP-PCA 神经网络模型的结果更接近于1，验证了PCA-BP 神经网络预测模型具有更好我的预测准确性。所以主成分分析法对于简化预测模型的输入，有利于提高预测精度。而且，PCA-BP神经网络预测模型预测结果也较好，具有一定的可靠性。

表5 模型预测结果

表6 不同模型的评价指标

4 结论

（1）本文在选取因素时充分考虑到了郑州市的市情，从15个因素中选取了10 个主要因素作为原始数据。

（2）以影响因子作为模型的输入会对预测结果产生影响，所以影响因子的多少对预测精度也会产生影响。本文引入了灰色关联分析和主成分分析法对用水量影响因素进行分析和处理，建立了PCA-BP 神经网络模型进行预测，与单一的BP 神经网络预测结果进行比较。通过结论可以看出，组合模型比单个模型的预测精度要好。

（3）本文在数据方面存在一定的问题。由于受到各方面限制，只收集到2002-2017 年的数据，数据较少，会在一定程度上影响模型的预测精度。

（4）改进方向。本文选取的是郑州市年用水量的预测，时间跨度较大，建议下一步在条件充足的前提下，缩小时间的跨度对郑州市用水量进行短期的预测。