多路信号的抗混叠滤波器设计
宋金玲 姜 苏 杜钟祥 席纪江 陈善恒 王洪梅
(1、中国矿业大学 信息与控制工程学院,江苏 徐州221116 2、徐州市第一人民医院,江苏 徐州221117)
软件无线电在应用中,往往需要同时处理不同频带上的多个射频信号,选择合适的采样频率是接收多频带信号的一个难点。大多数学者在处理多频段信号时,为了降低接收机后端对数字处理方面的负担,在信号频谱不混叠的前提下,尽量选取低采样频率。然而为了避免信号混叠,学者们致力于研究频率选择算法,这样做不仅加大了计算的繁琐程度,还在防止信号频率混叠方面限制了频率选择。另外采样精度会随着对信号采样频率要求越低而使得对RF 带通滤波器的要求增高。
为解决上述面临的问题,本文提出一种软件无线电多带通信号接收方法,实现了软件无线电对多带通信号无混叠接收的要求。具体的,用具有可调时间延迟的二阶带通采样来实现多路混叠信号的接收。该方法同时接收不同频带上的多个射频带通信号,对多频段带通信号进行先采样、后分离处理,允许采样后在同一频段内有多个带通信号的频谱发生重叠。
1 二阶采样理论及相位调整滤波器设计
1.1 二阶带通采样理论
一阶带通采样理论,假设待采样的射频带通信号为R(f),其带宽为B。采用采样频率fs为两倍的带宽,即fs=2B。所有在(n-1/2)fs<|f|<(n+1/2)fs频率区域内的信号,都定义为索引为n 的信号。经过带通采样,所有索引为n 的信号会映射到频率范围|f|
基于一阶采样的分析,可得到的中心频率公式为fc=(2n+1/2)B,带通采样后得到的采样信号为

带通采样描述的设计原理,使得原来的频谱数值在经过带通采样分析后,使其在频域范围内对折与复制。
若按照理想化的设计理念,即不出现信号的混叠现象,即两倍带宽值远小于采用频率,且信号为整数时,能够保证数值满足fc=(2n+1/2)B。这种限制使研究者提出了二阶采用的理念,借助于时间域上所产生的延时现象即频域上产生的相位差来进行带通采样。
二阶采样结构如图1 所示。

图1 二阶采样结构
带通信号经过二阶采样的采样信号值:
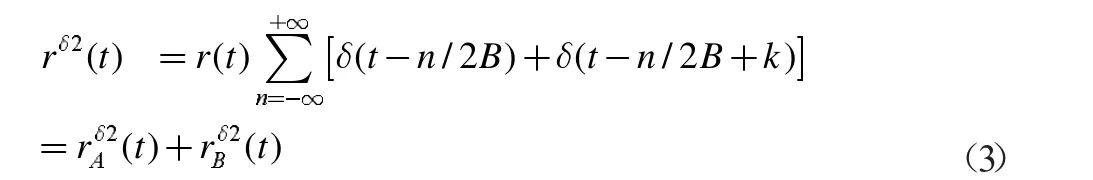
k 的值表示两种采样之间的产生的时间延迟,rAδ2(t)作为A 通道的采样信号,rBδ2(t)作为B 通道的采样信号。
其频谱为:

其中γ=e-j2πk2B。
带通信号R(f)的频谱用正数部分和负数部分进行表示:

带通采样描述的设计原理,使得原来的频谱数值在经过带通采样分析后,使其在频域范围内对折与复制,如图2,3 所示。

图2 通道A 中的正负频谱复制示意图

图3 通道B 中的正负频谱复制示意图
1.2 抗混叠滤波器设计
以两路带通信号为例,二阶带通采样两通道的频谱图分别如图4、5 所示,从图中可以看出,通道A 中两个信号频谱没有相角差异,而通道B 中由于ADC B 引入采样延迟的原理,两个信号R1(f)和R2(f)的频谱都分别产生了相角差γn1和γn2。利用两通道不同的相角差设计抗混叠滤波器FB1(f)和FB2(f),调整两信号相位,使得经过FB1(f)的输出信号叠加后信号R2(f)为零,而另一信号R1(f)不变,实现信号R2(f)的分离;经过FB2(f)的输出信号叠加后信号R1(f)为零,实现信号R1(f)的分离。

图4 A 通道采样频谱

图5 B 通道采样频谱
将抗混叠滤波器FB(f)应用于通道B。于是,恢复的信号频谱变为:

对每路通道来说,都存在来自n1和n2频率位置的信号,因此,公式(7)可以进一步分解为:
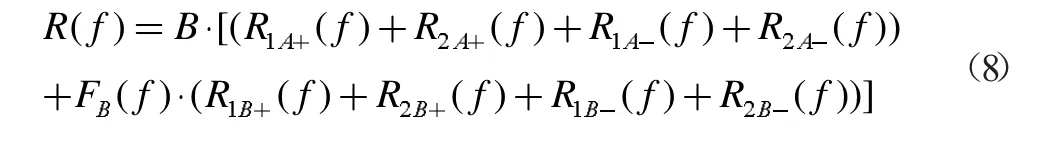
同时接收两路信号R1(f)和R2(f)的接收器包括两个可调的射频滤波器用来选择两带通信号,经过叠加后输入到采样器,两路信号R1(f)和R2(f)被同时采样,两个可重新配置的滤波器FB1(f)、FB2(f)用来消除信号混叠,并并列的输出R1(f)和R2(f)。
其中,滤波器FB1(f)设计用于恢复R1(f)而消除R2(f)。因此,滤波器FB1(f)应该满足:

因此,通过解式(9)和(10)可以得到FB1(f)如下式:
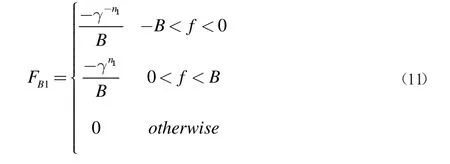
为了接收信号R2(f)而消除R1(f),需要设计另一滤波器FB2(f)。利用式(9),(10)所示的同样的方法可以得到FB2(f),如式(12)所示:

根据上述理论分析后,如下图所示,多路信号,只要保证混叠个数不超过两个,则可通过同样的方法设计相位调整滤波器,实现混叠信号分离。

图6 BPS 后的频谱
2 混叠分析与约束条件
2.1 混叠分析
假设一个RF 信号的中心频率为fc,以采样频率fs进行带通采样,则可以将第一个奈奎斯特区的中心频率(称为镜像频率)定义为

这里[·]表示舍入。
假设两个个带通信号同时以fAF1,fAF2和镜像频率进行接收。图7 显示了镜像频率和采样频率fs之间的关系。
考虑信号fAF2,有不同的fs选择,它具有三种混叠方式:
通过零频率附近的自镜像频谱进行混叠,如图7 的区域A所示。
通过周围的自我图像频率进行fs/2 频率混叠,如图7 的区域B 所示。
通过另一个信号进行混叠,如图7 的区域C 所示。
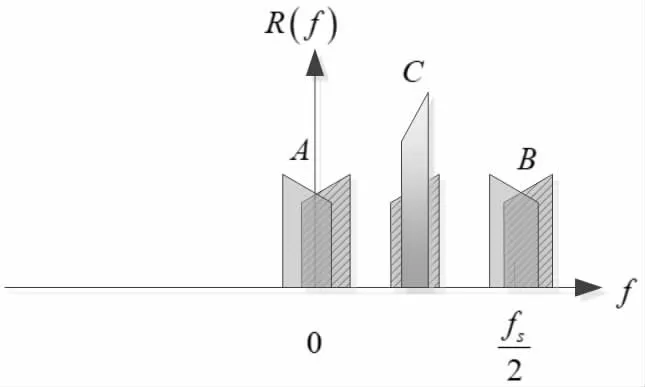
图7 信号混叠示意图
传统的选择fs方式是为了避免各种混叠,这会限制fs,并且通常需要进行大量计算。在小节1 中,可以通过软件解决两个信号重叠引起的镜像频谱混叠。因此,在选择fs上,允许的限制条件会较少。
2.2 约束条件
根据上述规则,给出了采样率约束条件,以允许采样后在同一位置出现两个混叠信号。可以通过以下公式进行详细的表示[7]:

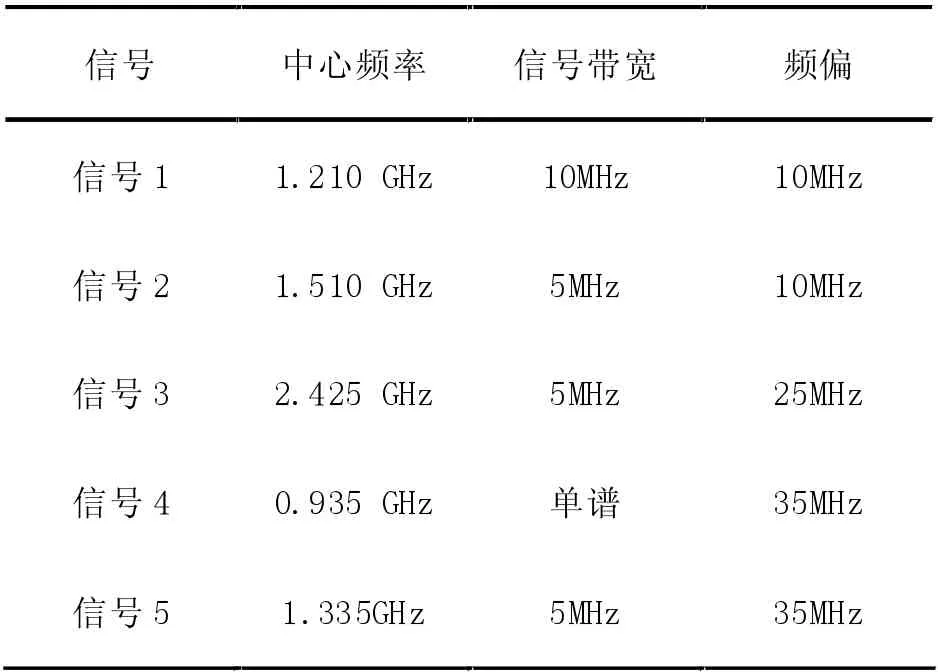
2)如果fDFi 如果fDFi>fs/2-(Bi/2+BG),然后fDFj 这里i=2,3…N,j=2,3…i-1。 3)a)如果fAFli>fAFlj,然后fAFhk b)如果fAFli c)如果fAFli 这里i=2,3…N,j=1,2,3…i-1,k∈[1,N],k≠i,k≠j。 在上述约束条件下,Bmax代表N 个带通信号的最大带宽;BG代表保护带宽;Bi,fDFi,fAFli和fAFhi分别代表BPS 之后的第一个奈奎斯特区域中信号i 的带宽,中心频率,最小频率和最大频率。 约束1)表示为采样频率要比信号加上保护带宽的最大带宽大两倍。 约束2)表示为仅仅一个信号发生镜像混叠或者fs/2 边界混叠。 约束3)表示为仅发生两个信号在同一位置混叠。 以5 个输入信号为例,参数如表1 所示。采样频率为100 MHz。两个采样通道之间的时间延迟为4×10-10s。 表1 五个输入信号的参数 带通采样(BPS)之后,采样信号1 和信号2 在10MHz 处进行重叠,信号4 和信号5 在35 MHz 处进行重叠,如图8 所示。 图8 BPS 后的信号频谱 应用小节1 中设计的抗混叠滤波器后,可以分离出重叠的信号。 在图9 中,信号2 和信号5 被抑制了,而信号1、信号3 和信号4 被保留了。 图9 抗混叠滤波器FB1 之后的信号频谱 在图10 中,信号1 和信号4 被抑制了,而信号2、信号3 和信号5 被保留了。抑制效果超过30dB。 图10 抗混叠滤波器FB2 之后的信号频谱 设计并使用进一步的低通或高通滤波器,可以分离五个信号。 基于带通采样定理,给出了延时可调的二阶带通采样的结构。通过设计抗混叠滤波器,可以分离出多个个重叠的信号。仿真结果表明,设计的抗混叠滤波器可以有效消除信号引起的混叠现象,解决的带通采样中多路信号混叠问题。3 多频段接收机的仿真结果



4 结论

