软件试验缺陷预测模型研究

何斌

（河北省秦皇岛市91404 部队，河南 秦皇岛066000）

1 概述

近些年，软件密集型系统在装备中的占比迅速增长，且这一趋势正在加快，软件已成为装备组成的主要部分。在实际装备使用中发现，系统发生故障或失效更多的是由于软件缺陷引起的，软件缺陷率成为影响软件可靠性的关键。按现有装备管理流程装备软件经过自测试、第三方软件测试、装备试验等过程，可以认为软件缺陷率降为较低的水平，但实际上交付部队的装备软件缺陷率可能仍处在较高的水平且这一状况无法准确计量。如何有效分析预测装备软件缺陷率已成为软件试验可靠性评价的重要研究内容。

Rayleigh 模型是一种常用软件缺陷分析预测方法。Rayleigh分析模型通过生命周期各阶段缺陷发现情况得到缺陷Rayleigh曲线，用于评估软件质量、预测软件现场质量。所以Rayleigh 模型可对装备软件缺陷分析预测并用于软件试验可靠性评价，是一种有效软件质量评估方法。但在实际工作中发现两方面问题限制了Raleigh 分析的应用，一方面在试验阶段很难准确采集生命周期各阶段缺陷数据尤其是开发与自测试阶段的数据；另一方面基于试验阶段可获取的软件缺陷数据（主要为软件测试、软件试验缺陷数据）与Rayleigh 模型分析结果有一定的出入。为解决上述问题本文提出基于件测试与试验数据的Raleigh 软件缺陷分析，并改进Raleigh 模型使其更加符合实际。

2 Rayleigh 模型

Rayleigh 模型可以预测软件开发全生命周期的缺陷分布，是一种常用的可靠性模型。Rayleigh 模型是Weibull 分布系列中的一种。Weibull 分布又称韦伯分布、韦氏分布或威布尔分布，由瑞典物理学家Wallodi Weibull 于1939 年引进，是可靠性分析及寿命检验的理论基础。Weibull 分布的标志性特征之一是其概率的尾部逐渐地趋近于零但达不到零。Rayleigh 模型应用于软件可靠性评估领域，主要利用软件缺陷在软件生命同期时间的分布符合Rayleigh 曲线的规律。

Rayleigh 模型的累积分布函数（CDF）和概率密度函数(PDF)为：

3 用于软件试验评估的Rayleigh 模型改进

通常情况在软件试验阶段，试验人员能较为准确地掌握软件测试缺陷及试验数据，故研究基于这两组数据Rayleigh 缺陷分析有较强的现实意义。通过研究大量过往的装备软件测试与软件试验缺陷数据发现，软件缺陷数据整体上并不符合Rayleigh 曲线。实际装备软件缺陷示意曲线如下：

图1 实际软件测试及试验缺陷分布图

实际装备软件测试与试验缺陷数据有以下几个特点：

（1）整体上并不符合Rayleigh 曲线；

（2）单组缺陷数据仍符合Rayleigh 曲线；

（3）软件测试发现累积缺陷通常高于软件试验发现累积缺陷。

分析形成这一现象主要原因为：软件测试与软件试验分别由不同的人员组织实施，在工作经验、知识结构上有差异且互补；软件测试与软件试验在测试方法及实施环境上有巨大的差异；软件测试在开展在软件试验之前能发现大量易发现缺陷。

综合上述原因，对用于软件试验评估的Rayleigh 模型进行如下改进：

（1）缺陷数据主要基于软件测试与软件试验发现的数据；（2）Rayleigh 曲线由软件测试数据与软件试验数据两组相对独立的数据组成，缺陷总数K 由两组按比例构成，即：

K=Ki+Kj

式中：Ki为软件测试发现累积缺陷，Kj为软件试验发现累积缺陷，按经验Ki≈K*0.8。

按实际对模型改为：

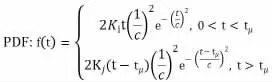
式中：tμ为软件测试时间（周数）。

4 改进模型实例验证分析

利用改进后的Rayleigh 模型在试验阶段对“XXX 型雷达软件”进行缺陷预测。此雷达软件进入性能试验之前已完成软件测试，测试周期为7 周。软件测试发现缺陷分布如下表所示：

表1 软件测试发现缺陷分布

根据改进后的Rayleigh 模型，软件试验阶段软件缺陷预测为72。使用Rayleigh 模型生成的模拟值见表2、表3：

表2 软件测试发现缺陷与Rayleigh 模拟缺陷表

表3 软件试验发现缺陷与Rayleigh 模拟缺陷表

Rayleigh 模型模拟密度函数（PDF）与实际数据图如图2 所示：

图2 PDF 模拟值与实际数据图

通过实例数据比对，改进后的Rayleigh 模型模拟数据与实际数据分布形状基本一致，数值误差处于可接受范围之内。

5 结论

作者通过软件测试与试验实际经验数据对Rayleigh 模型进行了改进。改进后的Rayleigh 模型更加符合软件测试及试验缺陷发现规律，可以在软件试验阶段比较真实地对软件试验缺陷进行预测。通过实例验证了改新模型对软件测试、试验缺陷发现有更好的拟合度，可以有效指导软件试验缺陷预测与软件可靠性评估。

该模型尚有一些问题需进一步深入研究。下一步重点对已完成的软件测试及试验的项目数据进行挖掘分析，总结设定软件测试与试验发现缺陷的最佳数量比，从而更加精确进行缺陷预测。