基于混合GRASP 算法的输电网规划及方案综合评价研究

翟及第 刘恩彤 李抒轩 石 强 张潇予

（1、东北电力大学 电气工程学院，吉林 吉林132012 2、哈尔滨商业大学 计算机与信息工程学院，黑龙江 哈尔滨150000 3、中央财经大学 金融学院，北京100081）

近年来社会经济发展迅速，电力系统为我国社会经济发展提供了重要的能源支持，电力是社会发展的重要因素之一，影响着我们生活的方方面面[1]。长期以来，我国重发电、轻输电以及电网建设投资不足等因素造成了我国电网是电力系统发展中最薄弱的环节。因此，对输电网规划问题进行深入研究具有重大的理论意义和现实意义。规划部门首先应该对各个重要因素进行考虑，然后制定出几个可行方案，最后再经过充分的系统分析及比较后选定最终方案。

1 输电网规划问题描述

在己知条件下，根据当前的待选线路情况，确定出最优的输电方案。规划问题表达为下列数学模型：

目标函数：

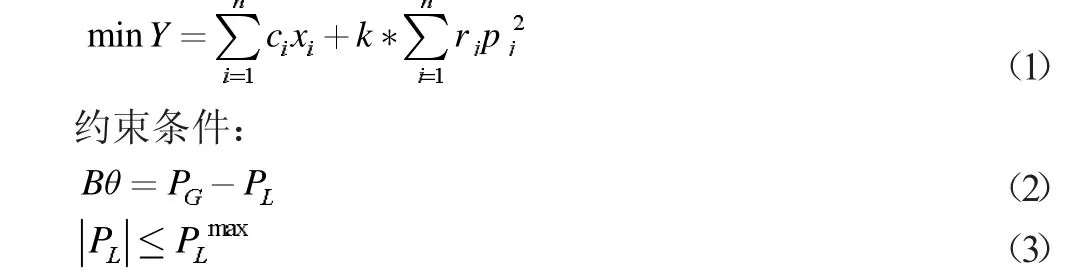
式中，Y 为年综合费用，其中第一项式子表示网络投资费用，第二项式子表示网络的功率损耗费用；xi为被选线路i 的长度；ci表示单位长度线路所需要的花费，单位是万元/千米；k 为年功率损耗费用系数；n 为加入新线路后网络线路总数；pj表示支路j 输送的有功功率大小；rj为支路j 的电阻；θ 为节点电压相角向量；B 为系统节点导纳矩阵；PG为发电机出力向量；PL为负荷向量；PLmax为正常运行时线路最大输送容量。

2 输电网规划模型的混合GRASP 算法

输电网仿真实现电网暂态、中长期过程的一体化仿真，可以将设备功能、设备电压以及设备电流等一次性发送给其他仿真设备中，同时，还能接收其他仿真应用所发送的操作事件，并对仿真结果进行处理和监测[2]。

结合GRASP 算法与SA 算法的优点，本文采用混合GRASP算法：GRASP 算法的局部搜索过程引入SA 算法的Metropolis 抽样策略，使混合GRASP 算法在局部搜索阶段可以按概率接受劣解，从而提高算法跳出局部极值的能力[3-5]。混合GRASP 算法的流程图见图1。

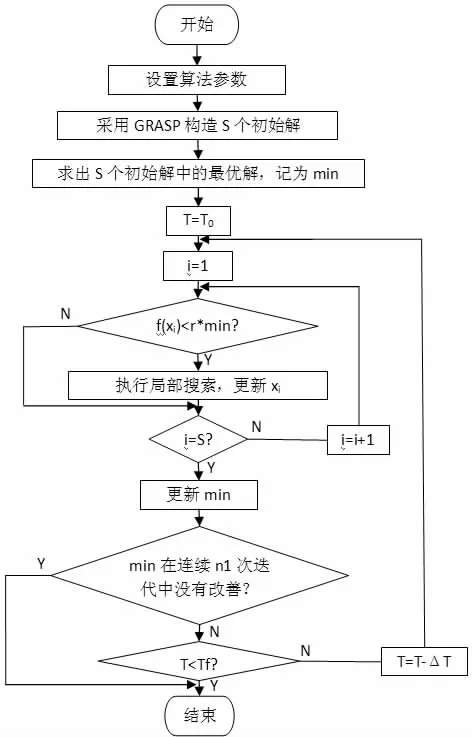
图1 混合GRASP 算法流程

3 算例分析

该算例采用被广泛研究的18 节点系统进行试验。该系统的网络结构图如图2 所示。应用MATLAB 软件需要设定如下参数：构造阶段产生可行解数量S=18；初始温度T0=700；终止温度Tf=10；温度下降步长ΔT=10；构造RCL 的百分比β=0.38；线路筛选系数r=0.5；每千米成本为25 万元。忽略线路电阻，因而不计网损费用。结果如图3 所示，该方案与文献[3]中的最优方案相同。

图2 18 节点网络结构

图3 算例规划结果图

表1 混合GRASP、GRASP 和AFSA 的计算性能比较

影响混合GRASP 算法性能的参数主要有构造可行解数量S、温度Tk、构造RCL 百分比β 等。发电机组爬坡能力，经常会对系统的调峰能力产生一定的限制影响[6]。18 节点系统为例，将这三种参数分别取为不同的数值进行仿真试验，研究它们对算法求解速度和收敛性能的影响。

（1）构造可行解数量S

将可行解数量S 取为不同的数值，研究其对算法计算时间和收敛性的影响，构造可行解数量越多，搜索就越充分，越容易收敛到全局最优。但构造解数量增加，运算时间增加，效率就会降低。因而，构造解的数量并非越多越好，应该视具体问题而定。对于18 节点系统而言，可行解数量在15 个以上，就能够获得最优方案。

（2）温度Tk

Metropolis 准则是混合GRASP 算法实现全局搜索的关键

技术，能使算法顺利跳出局部极值，并最终趋于全局最优。而温度Tk的大小是Metropolis 准则的核心：Tk很大时，算法在广域内进行搜索，当搜索到新解时对其不做任何判断而直接接受，即使这个并不比当前解更优；当Tk很小时，此时算法仅仅在一定范围内的局域里进行搜索，当搜索到新解时，首先将其与当前解进行比较，只有优于当前解才被接受。因此，算法的收敛性对Tk的选取要求很高。

（3）构造RCL 百分比β

输电网规划中，当β=1 时,每次取最优的线路完成加线操作，形成一个完全的贪婪过程；当β=0 时，每次的加线操作可以选择任何一条待选线路加入RCL，而不需对其有效性进行比较和分析，此时构造过程是一个完全的随机过程。一般情况下，β 取值为0.3～0.55 比较合理。

4 结论

根据GRASP 算法和SA 算法的特点，将其组合形成混合GRASP 算法。该混合算法结合了以上两种算法的优点，计算效率提高，收敛性能大大增强。根据输电网规划问题的特点，引入筛选机制，进一步提高了算法的计算速度。将该算法应用于求解输电网规划问题，仿真实例证明，具有很高的可行性与优越性。