直观想象素养下一道2020高考试题的解法探析
江智如 叶 蓉 蔡 珺
福建省南平市高级中学 (353000)
1.试题呈现
(2020年高考全国Ⅰ卷理科第11题)已知⊙M:x2+y2-2x-2y-2=0.直线l:2x+y+2=0,P为l上的动点,过点P作⊙M的切线PA,PB,切点为A,B.当|PM|·|AB|最小时,直线AB的方程为( ).
A.2x-y-1=0B.2x+y-1=0
C.2x-y+1=0D.2x+y+1=0
2.试题分析
试题依托直线与圆的位置关系,考查圆的切线相关知识,考生可以从圆的几何性质角度思考求解,通过数学阅读,分析试题的图形信息,运用圆的图形相关性质结论,建立数与形的联系,构建问题的直观模型,探索解决问题的方法与思路[1].考查考生数形结合思想、化归与转化思想和运算求解能力.本文在直观想象素养下,对本试题的解开展探析.
3.试题解析
3.1 几何法
思路分析:借助直线与圆的图象,利用圆的切线几何性质求解.
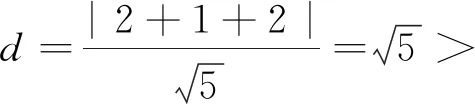

图1
2,所以⊙M与直线l相离.如图1作出直线l与⊙M的图象,连接AB,PM,交于点N.因为PA,PB为⊙M的切线且点P在⊙M外,所以由圆的性质得PM⊥AB且点N为AB中点,从而|PM|·|AB|=
2|PM|·|BN|.又在△PBM中,MB⊥PB,由面积法得|PM|·|BN|=|PB|·
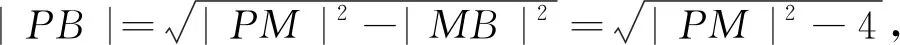

评析:试题由于动点较多,如果直接采用坐标法求解|PM|·|AB|的最小值,计算量大,不易求解.所以解法1考虑通过圆与直线的图形关系,利用圆的切线几何性质与直角三角形的几何性质,把两个“配角”动点A,B化归转化为“主角”动点P,把问题转化为圆心M到直线l的距离,得到AB∥l关系,最终得到结果.由于利用直线与圆的几何性质,求解过程中减少计算量,减轻考生的计算负担,考查考生数形结合思想、推理论证能力和运算求解能力.解法1要求考生具有扎实的几何功底,体现数学学习的能力与潜能[2],体现试题的区分与选拔功能,实现对考生直观想象素养和数学运算素养的提升.
3.2 托勒密定理法
思路分析:因为PM,AB是四边形PAMB对角线,所以考虑利用托勒密定理求解.
托勒密(Ptolemy)定理:在任意平面凸四边形ABCD中,均有AB·CD+AD·BC≥AC·BD,当且仅当A,B,C,D四点共圆时,等号成立.它揭示了平面凸四边形中对边和对角线之间的数量关系,广泛应用于解决几何与代数的问题[3].
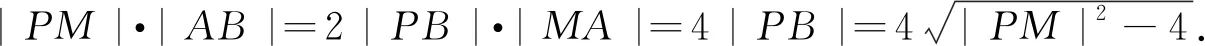
评析:解法2运用托勒密(Ptolemy)定理把问题转化为|PM|的最小值,然后利用圆的切线性质求解最终结果,计算量小,技巧性强,需要考生具有较强的数学学习潜能与继续学习的能力,体现考生数学思维与素养的差异.托勒密(Ptolemy)定理虽然不是高中数学的学习内容,但在各类竞赛和高考中,都有它的身影,如2008年高考重庆卷理科第4题[3],2018年4月福建省质检理科第16题[3]等,可以引导考生以“高观”的视角来学习初等数学,提高学习数学的兴趣,拓宽学习的视野,培养考生自主探究的能力,为考生的继续学习打下扎实基础,提升综合数学素养.
4.解法启示
试题语言精炼,逻辑严谨,依托几何图形,建立形与数的联系,将圆的定义、圆的切线、弦的性质等知识有机结合起来,在重视对解析几何基础理论知识考查的同时,侧重考查了考生数形结合思想和化归转化思想.试题已知条件的设计符合考生的学习实际,给考生提供了多种分析问题和解决问题的思路,引导考生通过有效的数学阅读,利用直观思维抓住圆的几何性质本质,在剖析问题本质的基础上,追求简洁的解题方法,力求解法来源于教材和已学知识,又高于已有知识,同时能够区分不同层次的考生,体现试题的区分与选拔功能,符合《课程标准(2017年版)》对解析几何内容的教学要求.在日常的教学实践中,教师应加强数形结合思想的训练,设置有效的“精致练习”[4],培养考生独立思考的习惯,发展几何直观与空间想象能力,增强运用几何直观与空间想象思考问题的意识,形成数学直观,在具体的情境中感悟事物的本质.

