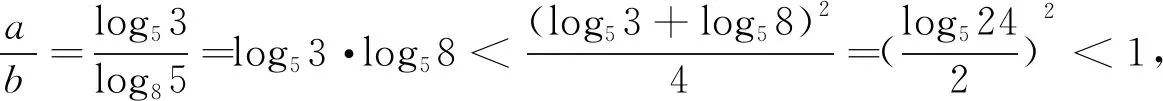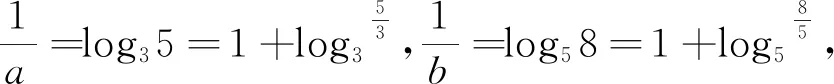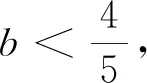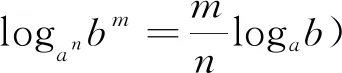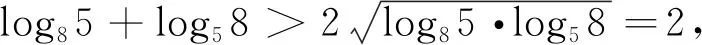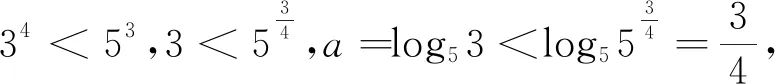不同视角解答一道2020高考填空压轴题
杜海洋
四川省成都经济技术开发区实验中学校 (610100)
普通高中《数学课程标准(2017年)》指出:“高中数学教学以发展学生数学学科核心素养为导向”,“提倡独立思考、自主学习、合作交流等多种学习方式”,“促进学生实践能力和创新意识的发展”.在教学过程中,对于某些典型问题,如果我们能够从多角度思考,会发现许多精彩的解法,从而领略数学的奥妙和魅力,提升学习兴趣,提高学习效率.尤其是一些经典的高考试题,因其“高大上”备受学生青睐,下面是笔者对2020年一道高考经典“小题”进行不同视角解答,让读者体会平时训练的指对互化、对数性质、比较大小的取“中间量”及常用方法的运用,真正感受解决高考试题的方法就源于平时训练的积累.
(2020全国Ⅲ卷第12题)已知55<84,134<85.设a=log53,b=log85,c=log138,则( ).
A.a C.b 分析:本题涉及指对比较大小,一般方法为若同底,考虑指数函数(或对数函数);若同指,则考虑幂函数,再利用函数的单调性比较大小;若不同底,也不同指,则其基本方法是“同底法”,即把不同底的对数式化为同底的对数式,然后根据单调性来解决,以及作商或作差或者利用中间量法,当然选择题利用排除法有时也非常奏效. b=log85=log8555 解法9:(利用中间量) 评析:本题考查了三个数大小的判断,指数对的运算和基本不等式的应用,考查了转化思想.指数、对数及幂的大小比较问题方法灵活,常常给人以“乱花渐欲迷人眼”的感觉,而对其问题进行归纳总结,会发现这类问题的解法往往可以从代数和几何两方面加以探寻,即利用函数的性质及图象解答,体现对数学抽象、逻辑推理、数学建模、数学运算及直观想象等核心素养的考查.