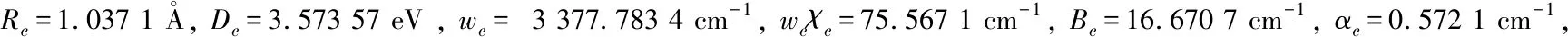NH自由基基态及低激发态从头计算研究

雷良建，万 冲，王兴炜，宋晓书

(贵州师范大学 物理与电子科学学院，贵阳 550001)

1 引 言

NH自由基是一种基本的非常重要的自由基，在太阳[1]、彗星[2]和星际大气[3]中都可以发现它的存在. NH自由基的性质已被广泛研究过，李权与朱正和[4]计算了NH分子基态及低激发态的分子结构与势能函数，施德恒等[5]采用多组态方法分析了NH基态的光谱常数，但是这些研究未对NH自由基基态及低激发态的振动能级及离心畸变常数进行计算. 在原子分子领域，分子的势能函数、光谱常数等一直是研究的热点[6-8]. 所以对NH自由基的势能函数，光谱常数进行研究有非常重要的意义. 本文利用耦合簇理论中的CCSD(T)方法和aug-cc-pv5z基组对NH自由基的基态(X3∑+)进行从头计算研究，拟合出了其势能函数，并对它的光谱常数we，weχe，Be，αe，Re，De进行了计算. 在得到势能函数后，通过求解径向Schrödinger方程，找出了当转动量子数J=0时的合理振动能级及离心畸变常数. 在计算NH自由基基态的基础上，利用二次组态相互作用中的QCISD(T)方法和aug-cc-pv5z基组对NH自由基的低激发态(b1∑+)进行从头计算研究，得到了NH自由基低激发态的光谱常数、振转能级、惯性转动常数及离心畸变常数.

2 势能函数计算

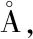
将得到的势能函数利用最小二乘法用Murrell-Sorbie势能函数[8]进行拟合，Murrell-Sorbie势能函的形式为:

V(ρ)=-De(1+a1ρ+a2ρ2+a3ρ3)exp(-a1ρ)

(1)

式(1)中De为离解能，ρ=r-Re，Re为平衡核间距，r为原子核之间的距离，a1，a2，a3为通过拟合得到的参数. 将拟合得到的参数列入表1中.

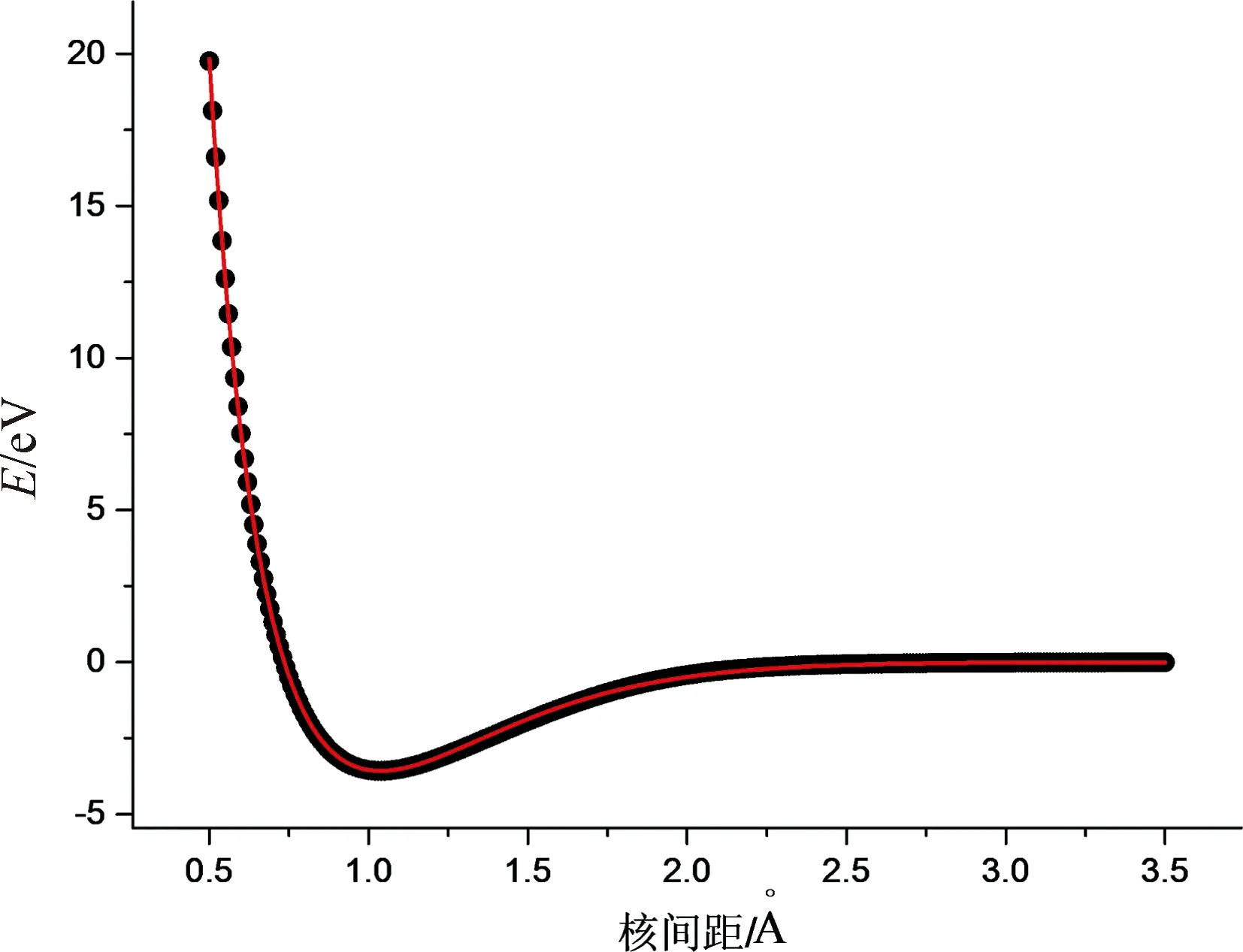
图1 NH自由基基态势能曲线Fig.1 The potential energy function for the ground state of NH radical

表1 NH自由基基态及低激发态Murrell-Sorbie势能函数参数及力常数Tab.1 Murrell-Sorbie potential energy function parameters and force constants for the ground and low excited states of NH radical

从图1中可以看出拟合的效果比较好，为了从理论上分析拟合的效果，我们引入了均方根误差(RMS)[9]，RMS的表达式为:

(2)

式(2)中,N为单点能扫描的个数，VAPEF为拟合值，Vab为从头计算的值. 通过理论计算发现RMS=16.76 cm-1,远低于化学计算要求的精度(不大于349.755 cm-1)[10].这说明本文的计算精度是比较可靠的，Murrell-Sorbie势能函数完全可以作为NH自由基基态(X3∑+)的势能函数.

图2 NH自由基低激发态势能曲线Fig.2 The potential energy function for the low excited state of NH radical

3 光谱常数计算

在得到NH自由基基态(X3∑+)及低激发态(b1∑+)的势能函数V(r)后，通过对势能函数V(r)的核间距r求二阶，三阶，四阶导数，得到了二阶力常数f2，三阶力常数f3，四阶力常数f4与a1，a2，a3的关系如下:

(3)

(4)

(5)

通过(3)～(5)式将计算结果f2，f3，f4列入表1中，将计算得到各阶力常数通过文献[11]中如下公式可以计算出NH自由基基态(X3∑+)及低激发态(b1∑+)的光谱常数，其结果如表2所示.

(6)

(7)

(8)

(9)

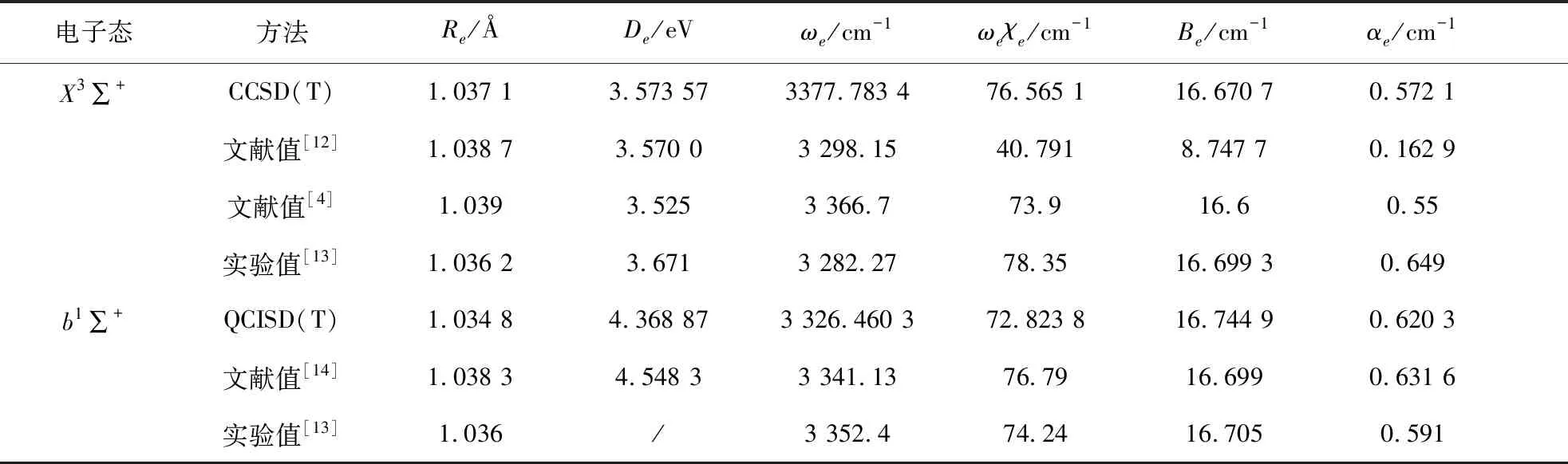
表2 NH自由基基态及低激发态的光谱常数Tab.2 Spectroscopic constantsof ground and low excited states of NH radical

4 振动能级的计算

在得到NH自由基基态(X3∑+)和低激发态(b1∑+)的势能函数V(r)后，将势能函数V(r)代入(10)式中，通过求解(10)式的径向Schrödinger方程可以得到NH自由基基态(X3∑+)和低激发态(b1∑+)的的振转能级.

Ev,JΨv,J(r)

(10)

式(10)中,v是振动量子数，J是转动量子数，某一振动能级下的Ev,J可用如下的幂级数表示[15]

Ev,J=E(v)+Bv[J(J+1)]-

Dv[J(J+1)]2+Hv[J(J+J)]3+

Lv[J(J+1)]4+Mv[J(J+1)]5+

Nv[J(J+1)]6+Ov[J(J+1)]7

(11)

式(11)中,E(v)是振动能级，Bv是惯性转动常数,Dv，Hv，Lv，Mv，Nv和Ov为离心畸变常数. 首先将NH自由基基态(X3∑+)的势能函数V(r)代入式(11)中，当转动量子数J=0时，可以利用Level8.0程序[16]对NH自由基基态(X3∑+)的振动能级进行计算，发现第45个振动态的能级值为28 098.258 2 cm-1，刚好小于离解能De的值，因此只有45个振动态符合要求，现将45个振动能级及惯性转动常数列入表3中.

在得到振动能级Ev,J后，根据(11)式，可以得到各个振动态的离心畸变常数,其结果如表4所示.

在对NH自由基基态(X3∑+)的振动能级及离心畸变常数的计算后，本文对NH自由基的一个激发态(b1∑+)的振转能级和离心畸变常数进行计算研究. 在转动量子数J=0时，发现第50个振动态的能级值为33 318.050 5 cm-1，刚好小于离解能De的值，因此只有50个振动态的值符合要求，现将当转动量子数J=0时的50个振动能级E(v)和惯性转动常数Bv列入表5中.

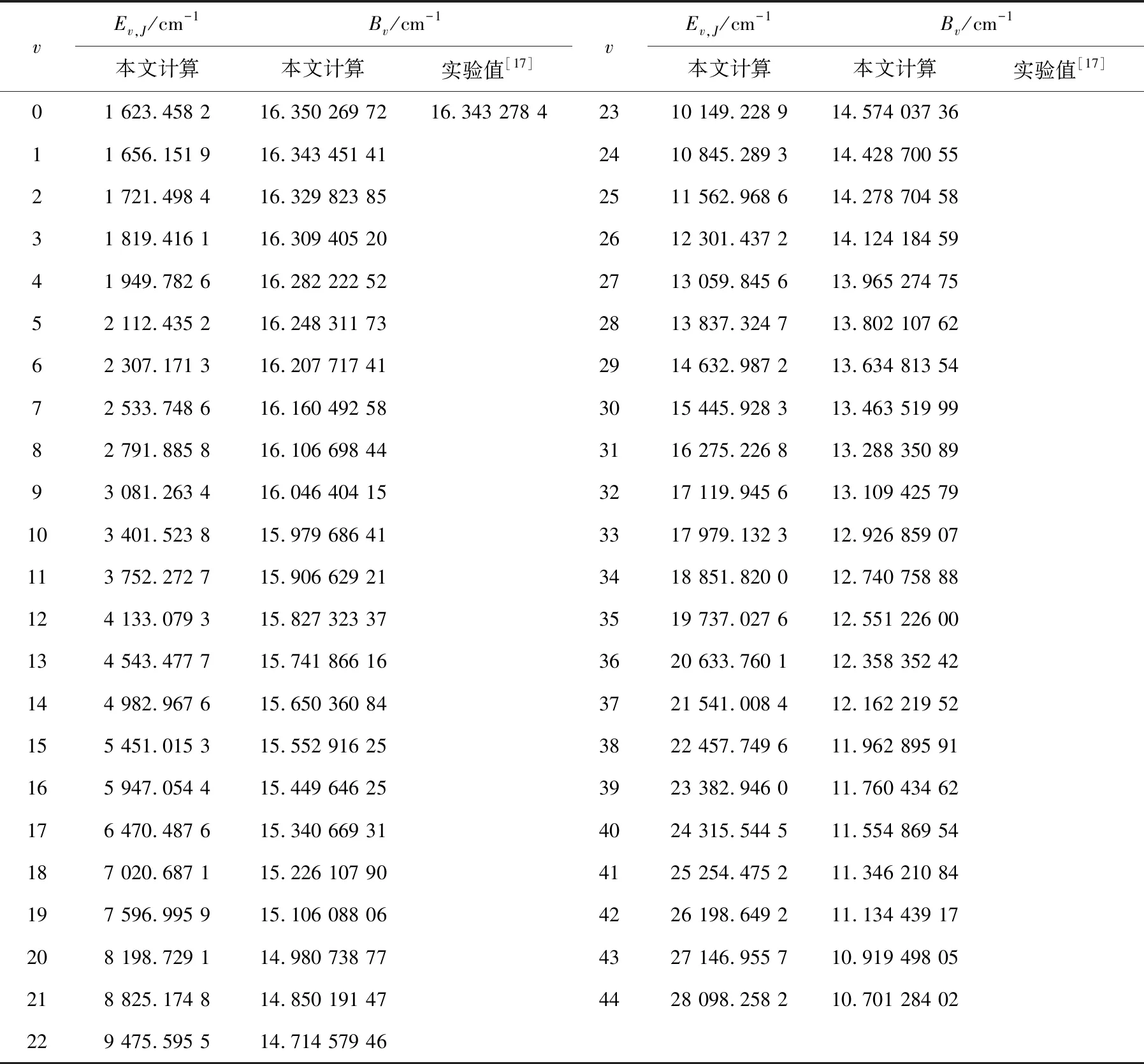
表3 CCSD(T)/aug-cc-pv5z理论下 NH(Χ3Σ+)自由基的振动能级和惯性转动常数Tab.3 Vibrational energy levels and inertial rotation constants of NH(Χ3Σ+) radical at the level of CCSD(T)/aug-cc-pv5z theory

表4 CCSD(T)/aug-cc-pv5z理论水平下 NH(Χ3Σ+)自由基的离心畸变常数(J=0)Tab.4 Centrifugal distortion constants of NH(Χ3Σ+)radical at the level of CCSD(T) /aug-cc-pv5z theory(J=0)

(续表4)381.3 045 4435.8 528 132-1.0 750 058-1.1 462 745-7.8 100 939-1.9 743 353391.2 912 4705.5 096 698-1.1 271 777-1.5 382 386-8.9 688 106-2.2 862 034401.2 784 6515.1 381 759-1.1 977 451-2.0 013 055-1.0 367 648-2.7 375 961411.2 663 2024.7 306 703-1.2 908 128-2.5 529 546-1.2 122 612-3.4 244 585421.2 549 6144.2 774 436-1.4 116 267-3.2 194 335-1.4 430 409-4.5 041 298431.2 445 7383.7 661 055-1.5 671 578-4.0 419 694-1.7 624 316-6.2 395 933441.2 353 8863.1 806 218-1.7 671 110-5.0 876 116-2.2 274 359-9.0 857 441

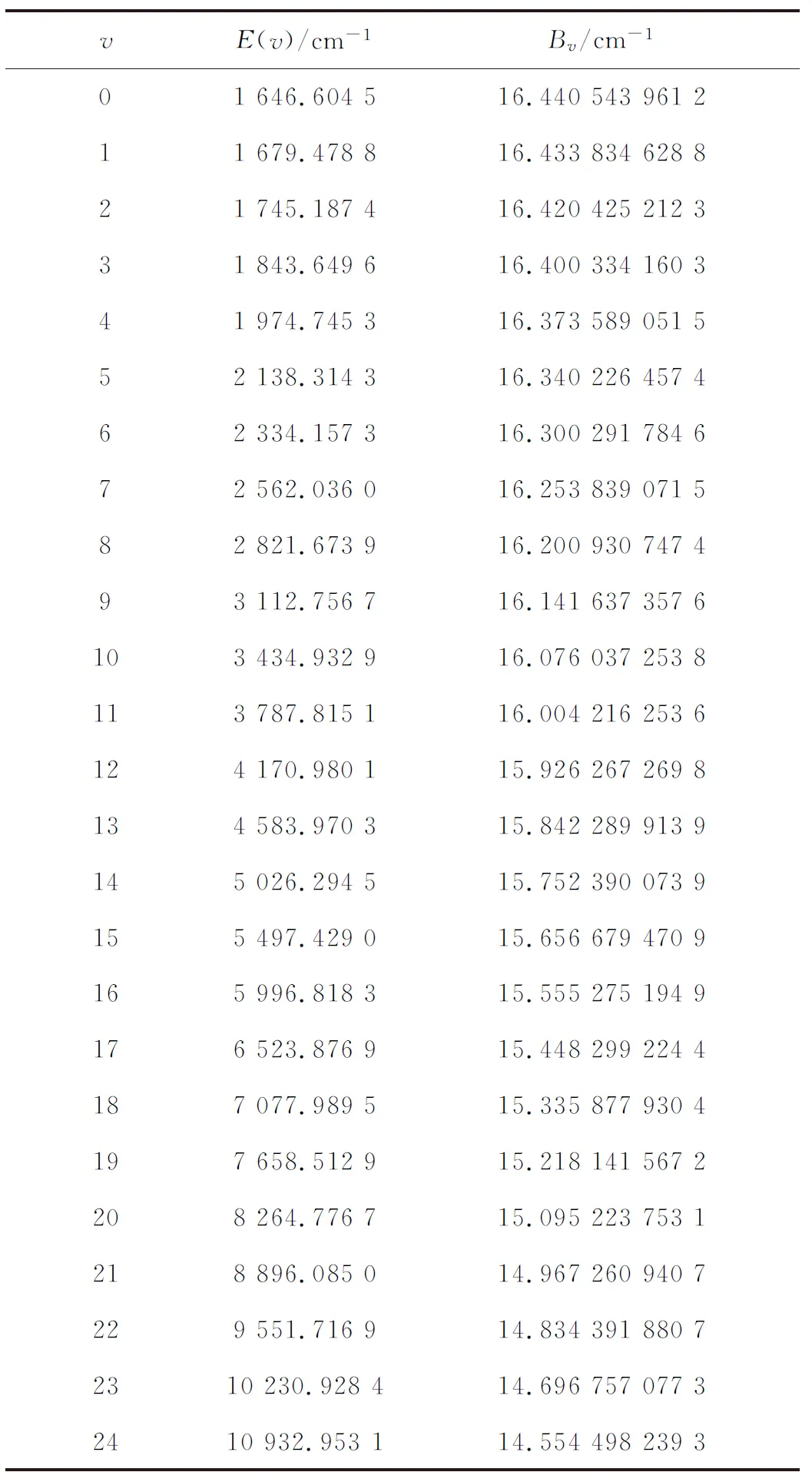
表5 QCISD(T)/aug-cc-pv5z理论水平下 NH自由基的振动能级和惯性转动常数Tab.5 Vibrational energy levels and inertial rotation constants of NH radical at the level of QCISD(T)/aug-cc-pv5z theory

(续表5)

在得到NH自由基激发态(b1∑+)在转动量子数J=0时的振动能级Ev,J后,可以根据(11)式计算其离心畸变常数Dv，Hv，Lv，Mv，Nv和Ov，其结果如表6所示.

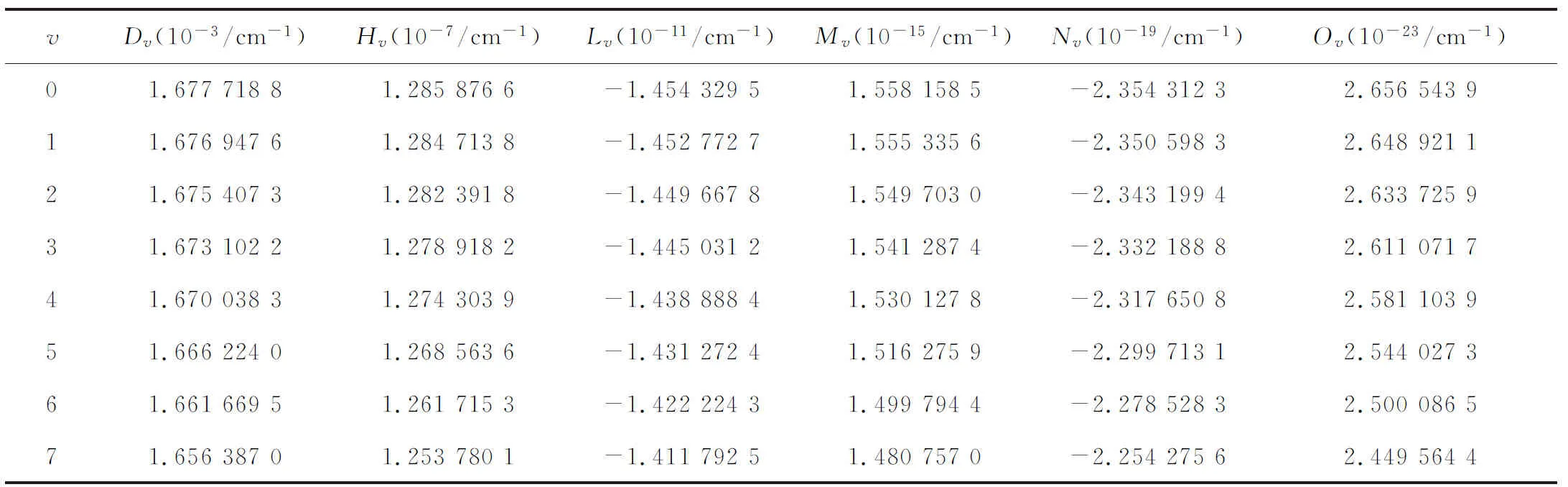
表6 QCISD(T)/aug-cc-pv5z 理论水平下NH自由基激发态离心畸变常数Tab.6 Centrifugal distortion constants of excited state of NH radical at the level of QCISD(T) / aug-cc-pv5z theory

(续表6)421.204 517 15.232 165 7-9.413 351 0-5.021 594 2-3.219 855 6-8.022 794 8431.191 439 34.904 206 7-9.666 903 4-6.818 650 2-3.768 263 2-1.029 694 1441.178 946 44.558 115 0-1.001 332 0-8.991 187 7-4.492 456 6-1.336 138 8451.167 133 14.189 665 2-1.047 616 0-1.166 649 0-5.460 276 2-1.757 928 4461.156 111 43.793 370 9-1.108 729 9-1.502 534 8-6.773 152 9-2.352 280 3471.146 015 23.362 018 5-1.189 065 9-1.933 033 8-8.586 824 8-3.212 085 1481.137 008 32.885 980 8-1.294 804 4-2.497 267 8-1.114 770 7-4.493 383 0491.129 294 82.352 179 2-1.434 852 4-3.255 257 8-1.485 931 4-6.468 806 0

5 结 论