加权Bergman空间到Bloch-Orlicz空间上的乘积型算子

陈 志，江治杰

(四川轻化工大学数学与统计学院，自贡 643000)

1 引 言

设D={z∈C:|z|<1}是复平面C中的开单位圆盘，H(D)是D上的解析函数集合.设φ是D到自身的解析映射，u∈H(D)，则由φ和u诱导的加权复合算子Wφ,u定义为

Wφ,uf(z)=u(z)f(φ(z))，z∈D，f∈H(D).

如果u≡1，那么Wφ,u变为复合算子，通常记为Cφ. 如果φ(z)=z，那么Wφ,u为解析乘法算子，通常记为Mu. 显然，Wφ,u=MuCφ，从而加权复合算子是乘积算子. 对于加权复合算子Wφ,u，人们常考虑的问题是如何通过φ和u的函数性质来刻画其有界性或者紧致性[1-8].

设n∈Ν0=Ν∪{0}. 众所周知，n阶微分算子定义为

Rnf(z)=f(n)(z)，z∈D，f∈H(D),

其中f(0)=f. 当n=1时，我们得到微分算子R. 文献[9]最先对乘积算子RCφ和CφR进行了研究. 此后人们又对它们进行了系统研究[10-13]. 目前，多种类型的乘积算子已引起了人们的广泛研究兴趣[14-23].

由乘法算子、复合算子和n阶微分算子可以定义如下六个乘积算子

RnMuCφ，RnCφMu，CφRnMu，MuRnCφ，

MuCφRn，CφMuRn

(1)

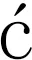
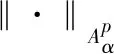
设Ψ是[0,+∞)上的严格单调递增凸函数，且满足Ψ(0)=0. 我们称f属于Bloch-Orlicz空间ΒΨ，如果存在某个依赖于f的正数λ，使得

该定义由Ramos Fernández在文献[5]中引入，其还证明了ΒΨ等距于μΨ-Bloch空间，其中

因此，在范数

下，ΒΨ是Banach空间.值得注意的是，ΒΨ推广了其它一些解析函数空间. 例如，如果Ψ(t)=tp(p>0)，ΒΨ是加权Bloch空间Βα，其中α=1/p；如果Ψ(t)=tlog(1+t)，ΒΨ则是Log-Bloch空间[29].

设X和Y是Banach空间. 称线性算子L:X→Y是有界的，如果存在正数K，使得

‖Lf‖Y≤K‖f‖X,f∈X.

进一步，称算子L:X→Y是紧致的，如果L把X中的有界集映射为Y中的相对紧致集.

文中我们约定

字母C代表正常数，且在不同情形下可以不同. 记号ab表示存在正常数C，使得a≤Cb.

2 主要引理

下面的引理刻画乘积型算子的紧致性，证明参见文献[30,命题3.11].

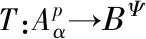
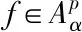
为了在加权Bergman空间中构造测试函数，对任意取定的w∈D，i∈Ν0，令

(2)

在下面的结果中，通过kw,i的线性组合，我们得到了需要的测试函数.

引理2.3设w∈D，n∈Ν.则对每一个固定的k∈{0,1,…,n+1}都存在常数a0,k，a1,k,…,an+1,k，使得函数

满足

(3)

其中j∈{0,1,…,n+1}{k}，且

(4)

证明 记a=(2α+4)/p. 我们首先证明该引理对k=0成立. 此时系统(3)等价于

(5)

其次，我们证明该引理对k≠0的情形也成立. 此时，系统3等价于

(6)

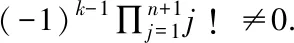
注1不难看到，当|w|→1时，{fw,k}在D的每个紧致子集上一致收敛到零.

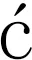
(f∘φ)(n)(z)=

(7)

其中Bn,k(x1,…,xn-k+1)是Bell多项式. 由(7)式和莱布尼兹公式，我们得到下面的结果.

引理2.4设f,u∈H(D),φ是D上的解析自映射，则

(u(z)f(φ(z)))(n+1)=

…,φ(j-k+1)(z)).

3 乘积型算子的有界性

定理3.1设α>-1，p≥1，u∈H(D),φ是D的解析自映射.下列陈述等价：

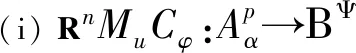
(ii) 对每个k∈{0,1,…,n+1}，函数u，φ满足下列条件：

C‖RnMuCφ‖

(8)

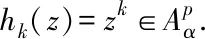
φ(j-l+1)(z))|≤C‖RnMuCφ‖

(9)

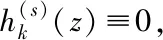
(10)

由式(10)，三角不等式及φ(z)的有界性，再注意到

的系数是独立于z的，我们得到

φ(j-k+1)(z))|≤C‖RnMuCφ‖

(11)

由数学归纳法，对每个k∈{0,1,…,n+1}，(11)式成立.

令w∈D，k∈{0,1,…,n+1}. 由引理2.3知，存在常数a0,k,a1,k,…,an+1,k，使得函数

满足

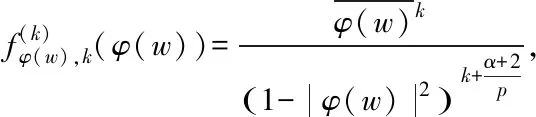
(12)

其中j∈{0,1,…,n+1}{k}，且

(13)

‖RnMuCφfφ(w),k‖ΒΨ≤C‖RnMuCφ‖

(14)

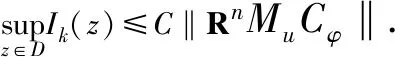
(15)

另一方面，由(11)式可得

(16)

故对每个k∈{0,1,…,n+1}，由(15)和(16)式可得Ik<∞.

(17)

显然，

(18)

由RnCφMu=RnMu∘φCφ，利用定理3.1和Faà di Bruno公式(7)可得到

推论3.2设α>-1，p≥1，u∈H(D),φ是D的解析自映射.下列陈述等价：

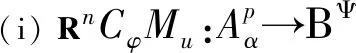
(ii) 对每个k∈{ 0,1,…,n+1}，函数u，φ满足下列条件：

注意到

(CφRnMuf)′(z)=

我们获得下面的结果.

定理3.3设α>-1，p≥1，u∈H(D),φ是D的解析自映射.下列陈述等价：

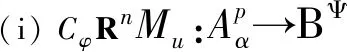
(ii) 对每个k∈{0,1,…,n+1}，函数u，φ满足

通过计算可得

[u′(z)Bn,k(φ′(z),…,φ(n-k+1)(z))+

u(z)Bn+1,k(φ′(z),…,φ(n-k+2)(z))]+

u(z)(φ′(z))n+1f(n+1)(φ(z)),

因而我们有如下结果.

定理3.4设α>-1，p≥1，u∈H(D),φ是D的解析自映射.下列陈述等价：

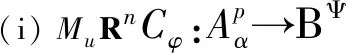
(ii) 对每个k∈{0,1,…,n+1}，函数u，φ满足

以及

由(MuCφRnf)′(z)=u′(z)f(n)(φ(z))+u(z)φ′(z)f(n+1)(φ(z))，我们还有下面的结果.

定理3.5设α>-1，p≥1，u∈H(D),φ是D的解析自映射.下列陈述等价：

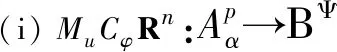
(ii) 函数u，φ满足

以及

注意到CφMuRn=Mu∘φCφRn，故由定理3.4可得

推论3.6设α>-1，p≥1，u∈H(D)，φ是D的解析自映射.下列陈述等价：

(ii) 函数u，φ满足：

以及

定理4.1设α>-1，p≥1，u∈H(D)，φ是D的解析自映射.下列陈述等价：

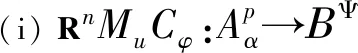
(ii) 对每个k∈{0,1,…,n+1}，函数u和φ满足Lk<∞，并且

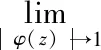
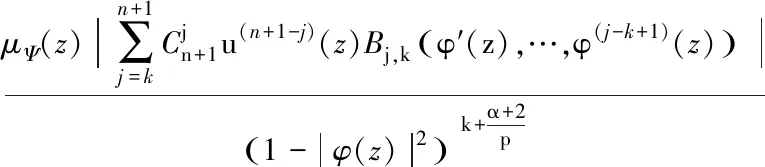
(18)

(19)

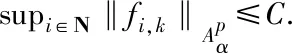
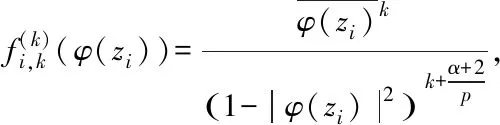
(20)

其中j∈{0,1,…,n+1}{k}.因此，由引理2.1，有

(21)

从而对每个k∈{0,1,…,n+1}，我们得到

(22)

(23)

其中k∈{0,1,…,n+1}. 由Lk<∞，以及式(23)，我们有

(24)

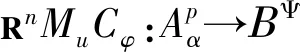
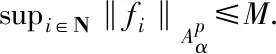
Bj,k(φ′(z),…,φ(j-k+1)(z))|≤

(24)

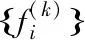
(25)

显然

(26)

故

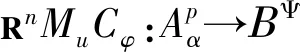
由定理3.1中Lk的定义以及RnCφMu=RnMu∘φCφ可得如下推论.

推论4.2设α>-1，p≥1，u∈H(D),φ是D的解析自映射.下列陈述等价：

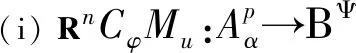
(ii) 对每个k∈{0,1,…,n+1}，函数u和φ满足

且

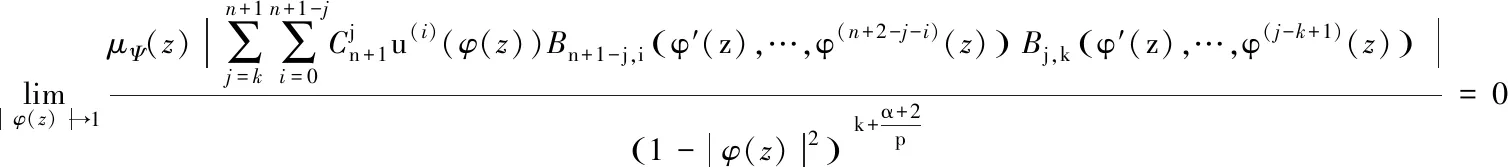
(27)

接下来的几个定理可类似定理4.1给出证明，这里统一省略.

定理4.3设α>-1，p≥1，u∈H(D),φ是D的解析自映射.下列陈述等价：

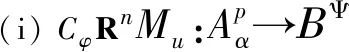
(ii) 对每个k∈{0,1,…,n+1}，函数u和φ满足

以及

定理4.4设α>-1,p≥1,u∈H(D),φ是D的解析自映射.下列陈述等价：

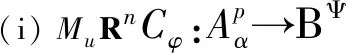
(ii) 对每个k∈{0,1,…,n+1}，函数u和φ满足

以及

定理4.5设α>-1，p≥1，u∈H(D),φ是D的解析自映射.下列陈述等价：

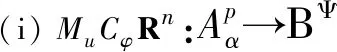
(ii) 函数u和φ满足u∈ΒΨ,

以及

推论4.6设α>-1,p≥1,u∈H(D),φ是D的解析自映射.下列陈述等价：

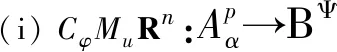
(ii) 函数u和φ满足u∈ΒΨ,

以及