错误探因问题反思现象解剖

钱小刚

数学学习中一个重要的思维品质就是反思。通过本章的学习，我们不仅要梳理、建构知识体系，如这一章各知识之间的联系，全等三角形与其他内容的联系，而且要学会反思，如在学习中有哪些典型错误，原因何在。只有不断总结、反思，才能完善知识结构，提升数学能力，减少甚至避免不必要的错误发生。下面是对同学们学习本章时的错误探因、问题反思和现象解剖，希望能对同学们的数学学习有所帮助。

一、在错误探因中掌握基本方法

在全等三角形判定中，有同学常常因为条件使用不当而导致出错。

例1 已知：如图1，点A、D、C、B 在同一直线上，AD=BC，AE=BF，CE=DF。求证：DF∥CE。

【错解】证明：在△AEC 与△BFD 中，

【错误探因】上述的证明运用了“SSS”，然而，条件中相等的线段都是三角形的边吗？显然，AD 和BC 不符合全等证明的要求。解决的办法是利用线段的和差关系将AD=BC 转化为AC=DB。

二、在问题反思中提升思维品质

不少同学混淆全等三角形两种表达方式，乱用边角对应关系而出错。

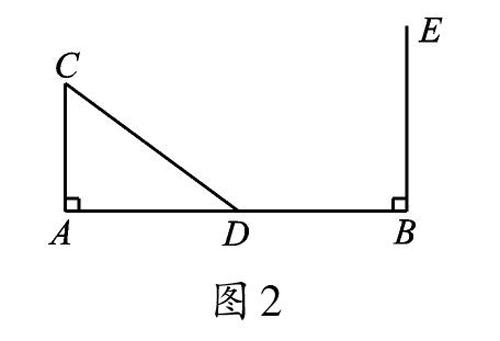
例2 如图2，∠CAB=∠EBA=90°，D在线段AB 上，AC=3，AD=4。若在射线BE 上存在点F，使△FBD 与△CAD 全等，求AB 的长。

【错解】由△FBD 与△CAD 全等得BD=AD=4，所以AB=AD+DB=4+4=8。

【问题反思】两个三角形的全等关系有两种表达方式，第一种是用符号表示，如“△FBD≌△CAD”;第二种是用文字表示，如“△FBD 与△CAD 全等”。这两种表达方式有明显的区别。第一种方式不仅表示这两个三角形全等，而且明确顶点F、B、D 与顶点C、A、D 分别对应，进而它们的3 条边、3 个角也分别具有对应关系。第二种方式只能说明这两个三角形是全等的，但没有明确顶点、边、角的对应关系。

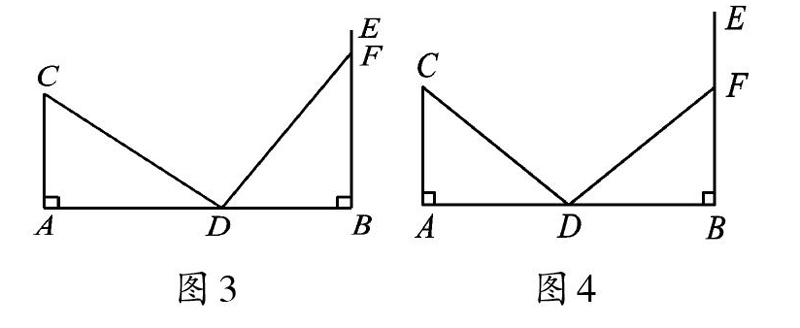
具体到本题，因为∠A=∠B=90°，所以顶点A 与B 是对应的，由“△FBD 与△CAD全等”得到两种情形，一种是△FBD≌△DAC（如图3），此时DB=AC=3，故AB=4+3=7;另一种是△FBD≌△CAD（如图4），此时DB=AD=4，故AB=4+4=8。

三、在现象解剖中优化思维方式

有些同学遇到通过全等三角形证明线段、角的关系时，难以合理利用条件和图形信息去正确、有效地构造三角形，导致出现思维障碍。

例3 已知：如图5，AD=BC，AC=BD。求证：∠D=∠C。

同学们在解决该问题时出现了这样几种现象：

【现象一】图形中有两个显性的三角形△ADO 与△BCO。要证明∠D=∠C，一些同学比较容易想到这两个三角形，但条件AC=BD 并非这两个显性的三角形的边，故难以证明它们全等，从而导致思路受阻。

【现象二】如图6，连接CD，用“SSS”证明△ACD≌△BDC，得到∠A=∠B 后，接下来有两种可能的情况：

一是结合条件∠DOA= ∠COB 和AD=BC，用“AAS”证明△ADO≌△BCO，从而得到∠ADB=∠BCA;

二是由∠ADB=180° - ∠A- ∠DOA，∠BCA=180°-∠B-∠COB 得到結论。

【现象解剖】出现这两种解题现象的根本原因是一些同学不能根据条件正确有效地构造三角形。

就“现象一”而言，当证明图中已知的三角形全等比较困难时，应考虑能否将欲证的边或角转化到其他三角形之中。结合条件“AD=BC、AC=BD”，结论“∠D=∠C”和图形发现，AD、∠D、BD 应该是△ABD 中“两边及其夹角”的关系，只要连接AB，便得到△ABD，同理得到△BAC，而这两个三角形的全等显而易见。

在“现象二”中，虽然能构成三角形，也容易证得它们全等，但由于没有合理利用图形，由所证得的全等三角形不能直接得出结论，导致证明过程烦琐冗长。