约束Hamilton 系统的对称性与守恒量的某些研究进展
郑明亮, 冯 鲜
(无锡太湖学院 机电工程学院,江苏 无锡214064)
当力学系统的Lagrange 函数的Hessian 矩阵不满秩(奇异动力系统),利用Legendre 变换,从Lagrange 体系过渡到Hamilton 体系描述时,在相空间中正则变量之间将存在固有内在约束(也称Dirac 约束),称为约束Hamilton 系统[1]。 现实中众多重要有用的系统均符合这类模型,它是力学界、控制界、数学界以及其他学术界共同关注的重要课题,它在近代理论物理(量子、光、电磁等)[2-4]、机械工程中机器人系统[5]、电力工业和自动化控制[6]等领域都有广阔的应用背景。 1940年末,Dirac[7-8]和Bergmann[9-10]首先开始了对此类系统的研究,他们最初的目的主要是为力学量子化和量子场论服务的。 近80年,约束Hamilton 系统动力学理论尤其是积分理论的研究得到了很大发展,取得了许多重要成果。 笔者在目前相关文献的基础上,就约束Hamilton 系统的对称性与守恒量问题进行总结归纳分析,并提出了进一步研究建议。
1 约束Hamilton 系统动力学的积分理论:对称性和守恒量
寻求力学系统的积分曲线是约束系统动力学的主要任务,其方法也是层出不穷和不断发展,从最初的场积分方法、势积分方法和雅可比最终乘子法到近代的各种对称性方法。 研究发现,系统的对称性和守恒量(首次积分、积分不变量等)紧密相关、相互影响。 通过系统对称性获得守恒量已是现代最实用普遍的方法。经典理论到量子理论的发展,将连续对称的研究(时空对称和内部对称)扩充到了分立对称的研究;微观领域规律的深入探索,将整体对称的分析扩充到了定域对称的研究。
1.1 经典水平下的对称性理论
1.1.1 变分原理与正则方程
对于约束Hamilton 系统,其结构特点就是存在固有内在约束[1,11]

此约束也必须满足虚位移和等时变分的限制性条件

固定边界条件的力学系统Hamilton 变分原理是指
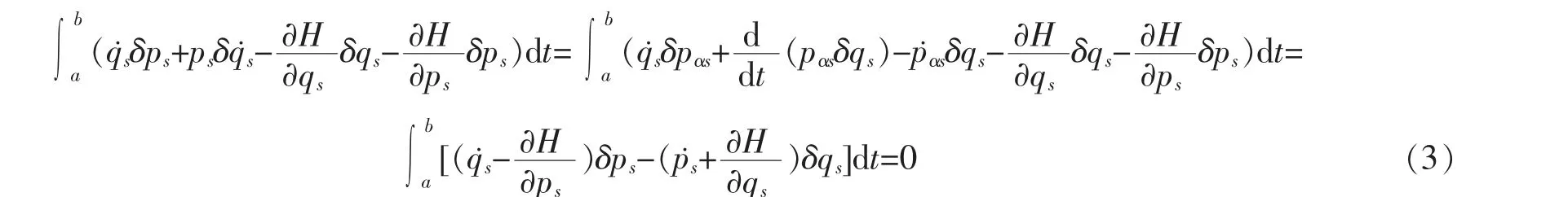
对于独立和非独立的qi、pi只要合理选择约束乘子λj,合并(2)和(3)式,则得系统正则方程为

其中HT=H+λjΦj称为总Hamilton 函数。 奇异系统正则方程(4)式必须与基于D'Alembert-Lagrange 原理得到系统的位形空间运动方程等价。
这里需要说明一下关于约束乘子λj的求解,系统内在约束随时间的演化应该是稳定的,初级约束的时间微商为零,即约束的自恰性条件为

(5)式可能出现:(I)是恒等式;(II)是约束乘子的完全确定方程;(III)不完全方程,需导出新的次级约束。
(I)和(II)情况较简单,这里不赘述。 对于(III)情况,由于出现新的次级约束

次级约束同样满足相容性条件,对于有限自由度系统,重复上述步骤,可逐次得次级约束依次为

1.1.2 Noether 对称性
Noether 对称性是指Hamilton 作用量在无限小群变换下的一种不变性[12-13]。 由Noether 对称性可找到守恒量;反之,由守恒量可找到相应的Noethar 对称性。
对于约束Hamilton 系统,考虑系统奇异性导致的固有内在约束的Noether 等式为
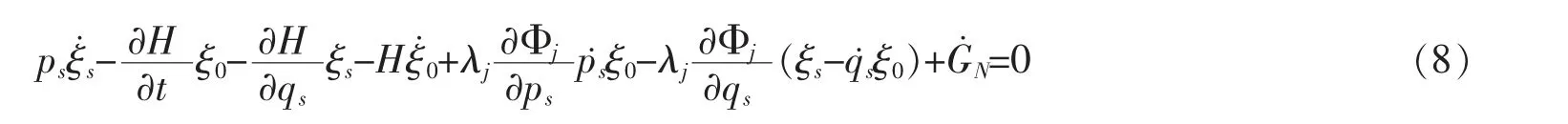
上式中虽不出现生成元函数ηs,实际上ηs可由ξ0、ξk表示
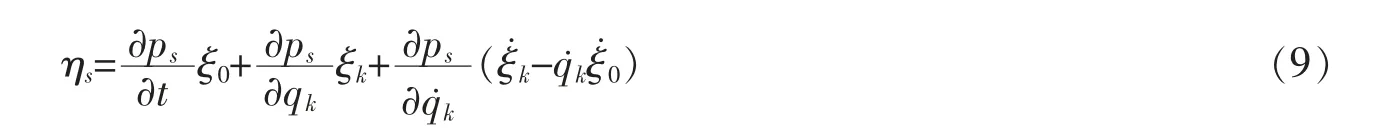
而Noether 守恒量有形式

对于非保守约束Hamilton 系统,Noether 等式需增加与非保守力相关的项,而守恒量仍有形式(10)[14-15]。对非完整系统,除Noether 等式外,生成元还要受到非完整约束的限制[16-17],守恒量仍有形式(10)。 要找到所有Noether 对称性也是不容易的,因为要解Killing 方程那样的偏微分方程。
问题1由Noether 对称性导出的守恒量被称为Noether 守恒量。 什么是非Noether 守恒量? 对于约束Hamilton 系统是否存在Noether 对称性还导致其他形式的守恒量?
1.1.3 Lie 对称性
Lie 对称性是利用系统的动力学方程在无限小群变换下的不变性寻求系统守恒量[18-19]。
对于约束Hamilton 系统,Lie 对称性的确定方程表为
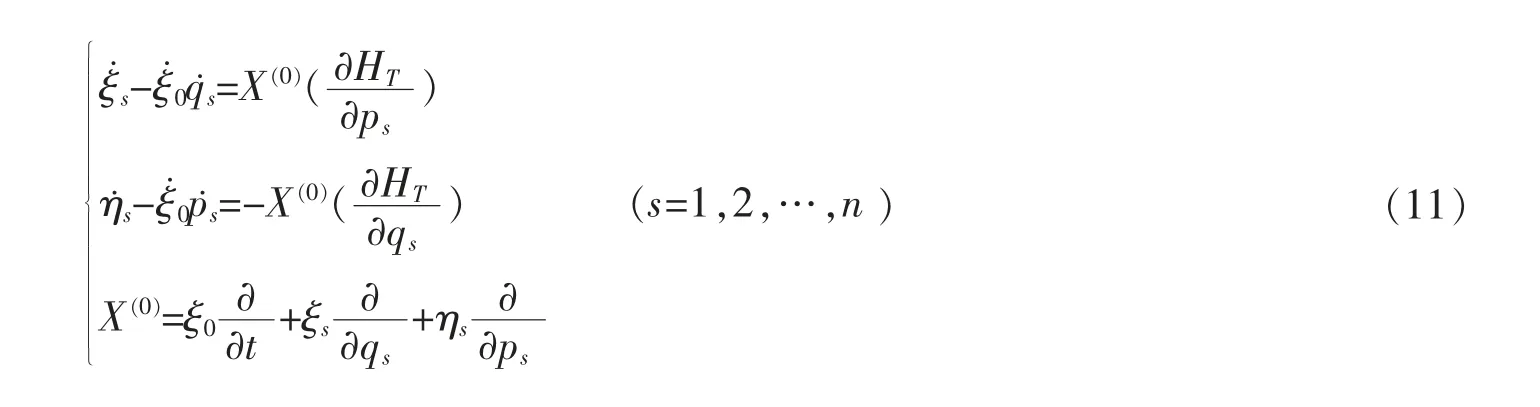
内在约束的不变性归结为限制方程为
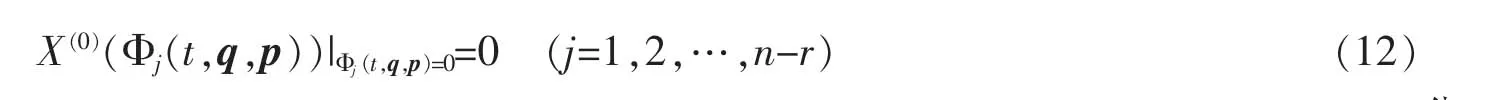
对于约束Hamilton 系统, 因为奇异性导致内在约束以及约束的限制条件, 需要将系统的Lie 对称性分成:Lie 对称性(生成元满足式(11))、弱Lie 对称性(生成元满足式(11)和(12))、强Lie 对称性(生成元满足式(11)、(12)和(2))。
Lie 对称性在一定条件下可导致多种形式守恒量, 若Lie 对称的生成元还同时满足结构方程即Noether等式(8),则约束Hamilton 系统Lie 对称同样导致Noether 型守恒量(10)[20]。
对于非保守约束Hamilton 系统,Lie 确定方程需增加与非保守力相关的项,结构方程也需要增加与非保守力相关的项,守恒量仍有形式(10)[21-22]。 对非完整系统,除Lie 对称确定方程和限制方程外,生成元还要受到非完整约束的附加限制,守恒量仍有形式(10)。
同时需要考虑,外在非完整约束对系统奇异性约束是否产生影响,进而影响系统的结构特点? 两者满足什么条件才可以相容?
问题2目前对于约束Hamilton 系统的守恒量都是集中在Noether 型,约束Hamilton 系统的Lie 对称性导致的Hojman 型守恒量以及新型守恒量的条件结构方程是什么?守恒量的形式与经典力学系统的Lie 对称性导致的Hojman 型守恒量以及新型守恒量有什么差异?
1.1.4 Mei 对称性
Mei 对称性是利用动力学方程中的动力学函数在无限小群变换下仍保持原方程形式不变寻求系统的守恒量[23]。
对于约束Hamilton 系统,满足的确定方程为
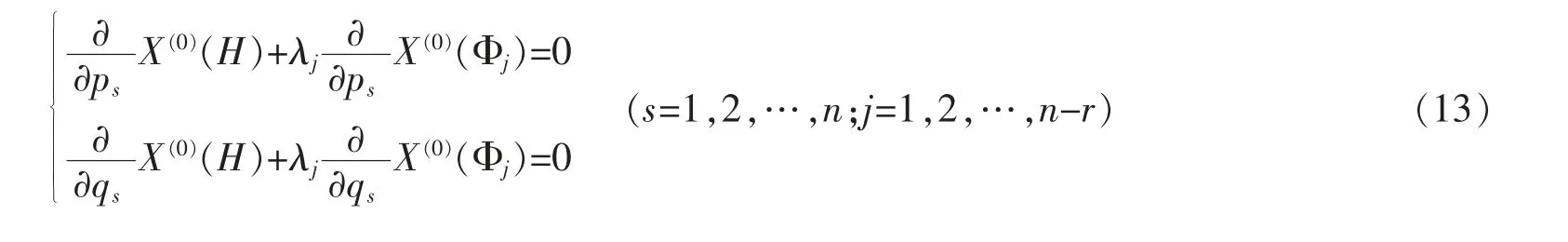
同样,内在约束的不变性归结为限制方程(12)。
对于约束Hamilton 系统,因为奇异性导致内在约束以及约束的限制条件,需要将系统的Mei 对称性分成:Mei 对称性(生成元满足式(13))、弱Mei 对称性(生成元满足式(13)和(12))、强Mei 对称性(生成元满足式(13)、(12)和(2))。
Mei 对称性在一定条件下也可导致多种形式守恒量, 若Mei 对称的生成元还同时满足结构方程即Noether 等式(8),则系统Mei 对称同样导致Noether 型守恒量(10)[24]。
对于非保守约束Hamilton 系统,Mei 确定方程需增加与非保守力相关的项,结构方程也需要增加与非保守力相关的项,守恒量仍有形式(10)。 对非完整系统,除Mei 对称确定方程和限制方程外,生成元还要受到非完整约束的附加限制,守恒量仍有形式(10)。 同时需要考虑,外在非完整约束对系统奇异性约束是否产生影响,进而影响系统的结构特点? 两者满足什么条件才可以相容?
问题3目前对于约束Hamilton 系统的守恒量都是集中在Noether 型, 约束Hamilton 系统的Mei 对称性导致的Mei 型守恒量的条件结构方程是什么? 守恒量的形式与经典力学系统的Mei 对称性导致的Mei 型守恒量有什么差异? 以及约束Hamilton 系统的Noether 对称性、Lie 对称性和Mei 对称性三者之间的关系说明又是怎样的?
这里需要注意,对于奇异系统,还有很多文献[13,19,25-34]只是在位形空间中研究其对称性和守恒量,并得到了丰富结果,它们的内容和结论形式不同于约束Hamilton 系统,由于奇异,这些在位形空间中成立的有些结论在约束Hamilton 体系中未必成立,这也是约束Hamilton 系统的又一大特点。
1.2 量子水平下的对称性理论
1.2.1 约束Hamilton 系统量子化
约束Hamilton 系统量子化问题的关键在于约束如何处置。 半个多世纪以来,已建立了多种算符形式和路径积分形式量子化。 目前用路径积分形式有突出的优点,传播函数或转换矩阵元中已不再出现算符(Q-数),出现在路径积分中的量均是经典的数(C-数)。 按照Dirac 的处理,将全部独立的约束(包括初级约束Φj和次级约束Φjk)分为第一类量和第二类量。一个与所有约束构成的Poisson 括号都等于0 的量称为第一类约束Λa,否则为第二类约束Ψb。选取m 个规范条件Ωa,满足

系统的量子化用独立变量q*和p*可通过正则变换得到

其量子跃迁幅为
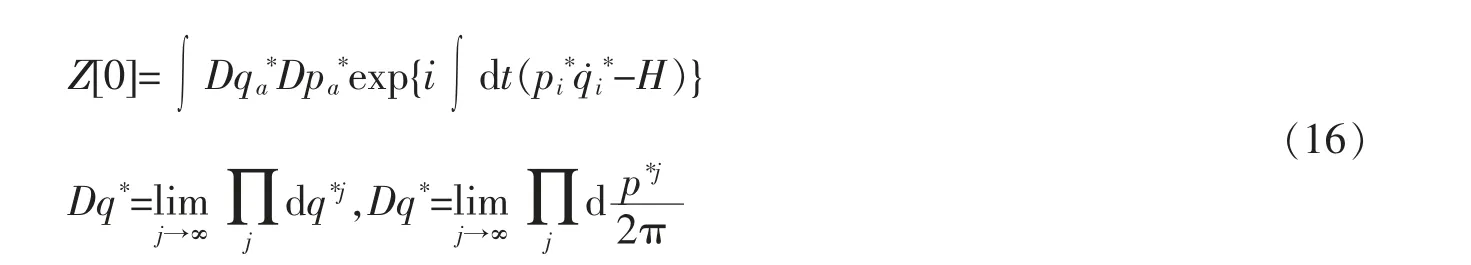
由于很难分离出真正的独立变量,利用δ 函数的变换性质以及正则变换下相空间体积不变,则系统路径积分形式下相空间Green 函数的生成泛函为

其中Ji、Ki分别为qi、pi的外源。
利用Grassmann 变量η(t)和η+(t)的积分性质,上式可简记为
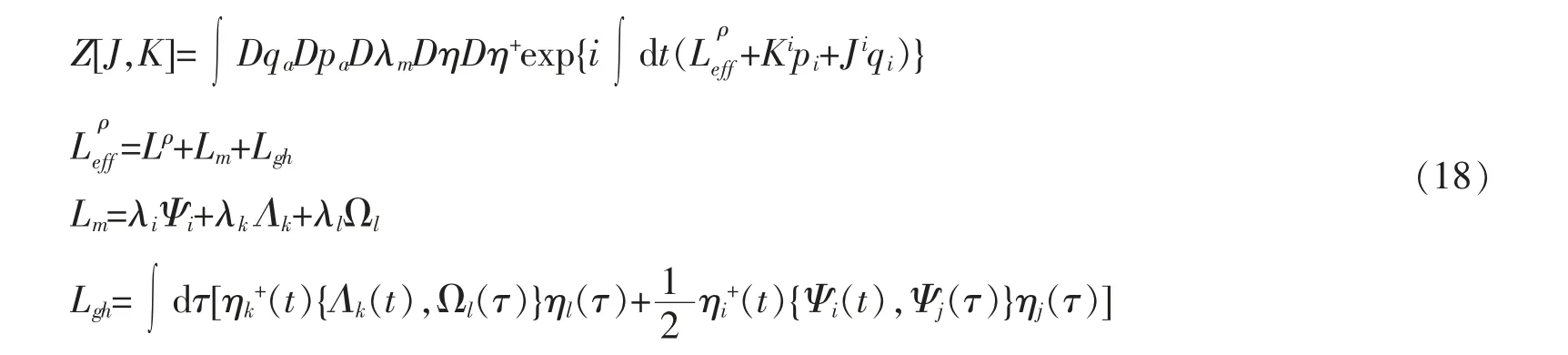
量子力学论中生成函数占基本地位,量子场的性质可由它出发来研究,如Feynmann 规则、Ward-Takahashi 恒等式、非微扰论、量子对称性质等。
关于约束Hamilton 系统的量子化有关详细叙述与应用研究可参看文献[35-39]。
1.2.2 量子正则对称性
在量子场论中Noether 恒等式对应于Ward 恒等式,它不仅是证明理论可重整化的重要工具,而且还在一些具体计算中(如QCD 中)也起重要作用。 约束Hamilton 系统中的Ward 恒等式可表示为
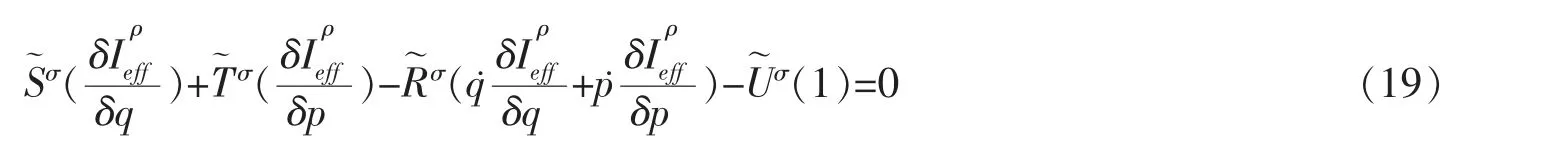
其中Sσ、Tσ、Rσ为无穷小定域变换的线性微分算符,~为伴随算符,而Uσ满足是无限小任意函数。 无论对称变换的Jacobi 行列式是否为1,此结果均与经典情形的结果形式上是不相同的,它是算符方程。 同时,无论是正规还是奇异,经典正则Noether 恒等式是一样的,但量子水平下,奇异系统时是需用代替。
在相空间中的整体变换下,如果系统的有效正则作用量准确到一个关于时间的全微分项是不变的,且对应的对称变换的Jacobi 行列式与无穷小任意函数无关 (路径积分测度在相应的变换下不变), 那么约束Hamilton 系统存在量子守恒律为

量子水平的守恒量不存在基态符号|0。 它与经典水平下的Noether 守恒律形式是一样的,但注意量子水平下奇异时用Heff代替。 同时它不同于量子正则Noether 恒等式转化为的量子(弱)守恒律形式,这一点又不同经典水平,经典水平下的Noether 恒等式和Noether 守恒量无直接关系,但量子水平下,Noether 恒等式可导致一类量子守恒律。
Poincare'-Cartan 积分不变量在经典力学和场论中有很重要的地位,它可以作为动力学的基本原理。 研究发现它与量子正则方程也是等价的。 在对称变换的Jacobi 行列式不为1 情况下,约束Hamilton 系统中的量子Poincare'-Cartan 积分不变量可表示为

其中T*是一种特定的遍时乘积,〈0|T*(∂μφ(x)∂vφ(y)…)|0〉=∂μ∂v〈0|T(φ(x)φ(y)…)|0〉。
上式存在基态符号|0,同时上述与经典理论不同的是,量子水平下,应由有效Hamilton 量Heff决定,它包含了规范条件。
关于约束Hamilton 系统的量子对称性有关详细叙述与应用研究可参看文献[40-50]。
2 总结与展望
为公式表达简洁,文中综述的约束Hamilton 系统对称性与守恒量的研究仅限于有限自由度,实际上约束Hamilton 系统的对称理论在连续介质系统和场论物理系统中应用也是十分广泛的。 笔者将约束Hamilton系统的研究从经典水平和量子水平两个方向并行出发,它们的很多研究思路和内容既有相似,又有很多差异,这正是奇异系统的一大本质属性。 笔者认为约束Hamilton 系统的理论进一步发展还有待于以下研究工作:(1)约束Hamilton 系统奇异性的物理解释与实验研究;(2)约束Hamilton 系统的对称性方程关于生成元的计算机大规模机械程序化求解;(3)约束Hamilton 系统的各种离散对称性和离散守恒量的研究,以及利用对称性构造高性能的数值方法;(4)用现代微分流形知识,对约束Hamilton 系统的对称性和守恒量作出几何动力学性态描述;(5)约束Hamilton 系统模型的对称性理论在工程实际问题中的应用价值。

