带最低保障的DC 养老金计划的最优投资
吕文欣, 董迎辉, 吴 桑
(苏州科技大学 数理学院,江苏 苏州215009)
保险公司也面临投资风险,关于保险公司所发行的具有投资功能的险种的定价方面已有了大量的研究[1-3],但在保险公司最优投资方面的研究并不多。 由于通货膨胀以及人口的老龄化,使得养老金的投资在近年来面临一定的风险,目前确定缴费型(Defined Contribution,DC)养老金计划因将投资风险转移给投保人而受到很大的关注。 DC 型养老金通过建立个人账户将缴费投资于金融市场,实现资金的累积和增值,以满足养老金给付需求。由于DC 养老金计划主要受退休前经济行为的影响,因此,DC 养老金管理者希望在资金积累阶段找到最优的投资组合。 很多文献都研究了DC 养老金的最优投资策略。
Boulier[4]等首次研究了常利率风险下DC 养老金的连续模型,并考虑CRRA 效用最大化准则下的DC 养老金的最优投资问题。 Dong[5]在卖空约束和组合保险条件下,研究了DC 养老金计划的最优投资。 王传玉[6]在DC 养老金终端财富外部保障约束下,引入欧式看涨期权,考虑随机通胀环境下的退休时刻终端财富期望效用最大化问题。 李仲飞[7]考虑了基于动态投资目标下DC 型养老基金在退休前累积阶段的最优资产配置问题。 Guan 和Liang[8]研究了损失厌恶和VAR 约束下DC 养老金的最优投资问题。 文章将考虑文献[6]中的DC养老金的利润共享原则,该原则将会导致参与DC 养老金计划的员工到期收益的非凹期望效用最大化问题。许多作者用凹化方法解决该问题[9-10]。 笔者将采用由Cox 和Huang[11]、Karatzas[12]等人提出的鞅方法,结合凹化方法来研究DC 养老金的最优投资组合问题。
论文结构如下:第一部分阐述了DC 养老金经理所面临的最优投资问题;第二部分利用凹化方法和拉格朗日对偶法得出带最低保障的最优终值财富及其财富过程;第三部分是结论。
1 优化问题
令(Ω,F,F,P)为一个带过滤的完备概率空间,其中F:={Ft}0≤t≤T,是一个满足通常条件的过滤。假设文中所有随机变量和随机过程都定义在该测度空间中。
假设金融市场上存在两种可交易资产:现金和股票。
设无风险现金账户在t 时刻的价格S0(t)满足方程

其中r>0 为固定利率。
设股票的价格过程如下

其中σ 为正的常数,W(t)是标准布朗运动。
养老金管理者在研究最优投资策略时,应该考虑从缴费者那里得到的缴费。 一般来说,员工的工资常常和金融市场有关,因此,这里考虑一个随机缴费率。 假设缴费率C(t)满足如下随机过程

其中μc、σc、C0均为正的常数。
假设x0为养老金账户的初始资金。 令π(t)和1-π(t)分别为投资在股票和现金的资金份额。 则DC 养老金计划的财富过程Xπ(t)满足

在到期收益分配时,将采用利润共享原则。 在该原则下,政府能够为参与养老金计划的员工提供最低保障收益,若资产价值高于最低收益,则参与养老金计划的员工应与政府共同分享盈余资产。 假设在T 时刻,DC 养老金计划提供的最低保障收益为G。 则在利润共享原则下,考虑最低保障的DC 养老金的终端财富值为

其中0<α≤1。
将在效用最大化原则下考虑DC 养老金的最优投资问题。 假设养老金管理者的效用函数为U(x),其中U 是在[0,∞)上严格递增、严格凹的连续可微函数,且满足
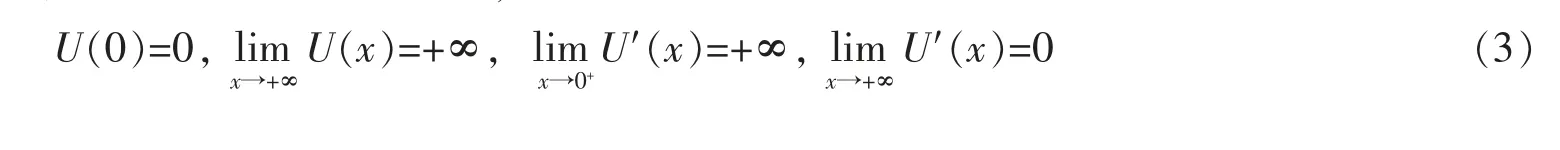
上述条件确保函数U′是严格递减的并且具有一个严格递减的逆函数I:(0,∞)→(0,∞),满足

定义1若对所有t∈[0,T],π(t)是一个F -循序可测的过程,且满足以及方程(2)存在唯一的强解Xπ(t),则称策略集{π:=π(t):t∈[0,T]}是可允许的。 用A 表示所有可允许的投资策略所组成的集合。
养老金经理的目标是通过使参与养老金计划的员工到期收益的期望效用达到最大化来寻找最优的资产配置。 因此,考虑下面的优化问题

2 DC 养老金的最优投资
为了求解优化问题(4),先来介绍完备市场的定价核。 由于金融市场是完备的,因此,存在唯一的定价核H(t)满足其中ξ=(μ-r)/σ。

为了确保最优投资策略的存在性,假设以下的可积性条件。
假设1假设对任意y>0,有E[U(I(yH(T)))]<∞并且E[I(yH(T))]<∞。
引理1对任意λ∈R,k>0,有

其中

β(t)=(r+(1/2)ξ2)(T-t),γ(t)=是标准正态分布变量的累积分布函数。
证明由(5)式可得

其中

则

经简单计算即得(6)式。
为了求解(4)式,定义

则在完备市场中,问题(4)可写为

注意到ψ(x)在[G,∞)上是凹函数,但在[0,∞)上并不是凹函数。 将运用文献[13]提出的标准拉格朗日对偶方法结合文献[7-8]提出的凹化方法来求解上述问题。
用fc表示在D 上f 的凹化包络

命题1ψ(x)的凹化包络ψc为
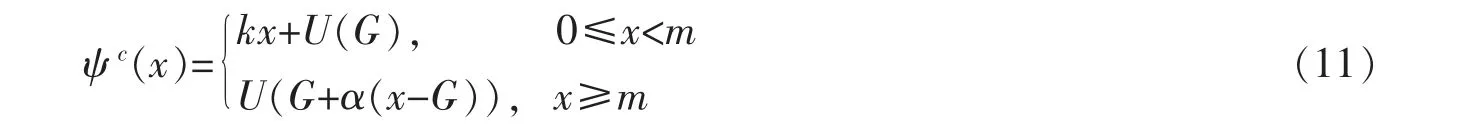
其中k=αU′(G+α(m-G)),m>G 是下列方程的唯一解

证明从点(0,U(G))作与ψ(x)相切的直线,切点记为(m,ψ(m))。只需证明方程(12)在(G,∞)上存在唯一的解。 记由于g′(x)=-xψ″(x)>0,所以g(x)是一个(G,∞)上的单调递增函数,并且


因此,方程(12)存在唯一的解m∈(G,∞)。
其中ψ(x)及其凹化包络函数ψc(x)的图像如图1 所示。

图1 ψ(x)及ψc(x)图像
命题2优化问题(10)的最优终值财富为

其中I(·)是U′(·)的逆函数,拉格朗日乘子β*>0 满足
证明问题(10)等价于如下问题

其中
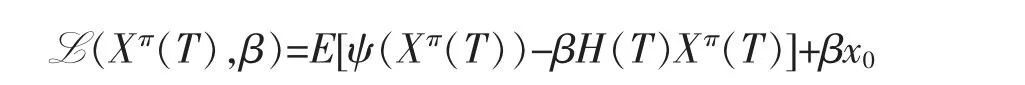
为了解决上述问题,先对固定的乘子β>0 来研究以下问题

通过逐点求解最优化问题,可以找到(14)式的最优解Xπ*,β*(T)。 仍需解决最优化问题

事实上,问题(15)的最优解β*可以通过对偶理论中的互补松弛条件直接得到。 首先,求解问题(14)。 对任意y>0,先解出的最大值点x*(y)。
由凹化方法及命题1 易得最大值点x*(y)为

则对每一个固定的β>0,问题(14)的最优解为
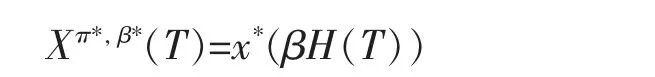
显然,V(β)=E[H(T)Xπ*,β*(T)]是关于β>0 的连续减函数,并且因此,存在唯一解β*>0 满足这意味着Xπ*,β*(T)是问题(10)的一个可行解。 仍需证明Xπ*,β*(T)确实是(10)式的最优解。 令Xπ(T)为满足(10)式中预算限制的任意终值财富。 则有

其中第一个不等式成立是由于

第二个不等式成立是由于对固定β*>0,Xπ*,β*(T)是问题(14)的最优解。
在求得最优终值财富后,可以求出最优财富过程和最优投资的表达式。
命题3最优化问题(10)在t 时刻的最优财富过程如下


其中β*>0 满足C(s)ds]=x0,d2(x,y,t)=d1(x,H(t),t)-γ(t),η(x,t)由(9)式给出,d1(x,y,t)由(7)式给出,φ 为标准正态分布的密度函数。
证明由资产定价的无套利理论可得

其中

将(13)式代入F1(t,H(t))并利用引理1 及(8)式得

由(1)式与(8)式可得
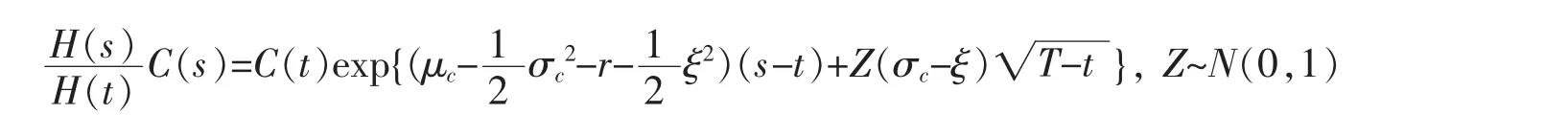
则立得

将(19)和(20)式代入(18)式可得证。
命题4最优化问题(10)在t 时刻投资于股票的最优比例为

其中

证明令Xπ*,β*(t)=F(β*,H(t),t),应用伊藤公式可以得到如下微分方程

比较(2)和(22)式dW(t)前的系数,即可得到最优投资策略。
3 结语
考虑在利润共享原则下带有最低保障的DC 养老金基于效用最大化原则的最优投资问题。 由于最低保障的存在,使得该效用最大化问题是一个非凹效用最大化问题。 笔者采用拉格朗日对偶方法以及凹化技巧解决了DC 养老金的最优投资组合问题, 给出了DC 养老金计划的最优财富过程和最优投资策略的通式表达式。

