基于相位相关方法的像移估计精度研究

张晗 谢妮慧 于飞 杨进

（北京空间机电研究所，北京 100094）

0 引言

随着星载遥感相机的分辨率由1～2m向着0.1m量级的不断提高，卫星抖动已经成为制约高分辨率遥感成像的关键瓶颈[1]。国内目前像移估计在实际应用的场景精度均不高，且多应用于车载成像系统，估计精度达到0.5个像素。应用于航天遥感的，如：“高分五号”卫星对日成像跟踪控制器，估计精度仅1个像素[2-3]。而针对高分辨率遥感图像的清晰化处理，像移估计精度要达到0.1个像素，如图1所示。本文将结合现有像移估计算法，分析影响算法估计精度的若干条件，获得高精度像移估计实现方案。

图1 不同精度下的图像清晰度Fig.1 Image sharpness with different precision values

比较经典的图像像移估计算法是块匹配法[4-5]，它具有精度高、实现简单的优点，但其计算量庞大，所以无法用于实时性要求较高的场合[6]。灰度投影法[7]是对块相关法的改进，虽然实现效率高，但其测量误差会随着图像的位移增加而增大[8-9]。相位相关法[10]利用图像的频域信息，其相关峰具有单峰值特性，很容易检测，且其计算精度与运算量和图像的位移大小无关[11]，本文即采用此种方式来实现稳像。

相位相关算法必须作用于高速CCD相机拍摄的连续帧图像。主要原理如图2所示。

实际CCD相机与主成像相机同轴同步对地成像，但主成像相机所成图像为遥感图像，成像尺寸大、曝光时间长，卫星在成像期间的抖动无法被准确记录[12-13]。卫星平台抖动功率谱密度汇集在图3中，包括美国“陆地卫星四号”（Landsat-4）测量值、欧空局“奥林普斯”卫星（OLYMPUS）测量值、日本“工程试验”卫星ETS系列（ETS-VI）实测值、国际空间站的有限元分析值等[14]。

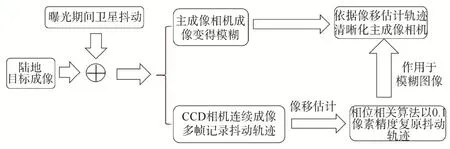
图2 利用像移估计实现遥感图像清晰化原理框图Fig.2 The schematic of image motion estimation to make the remote sensing image clear

图3 各种平台的功率谱密度曲线Fig.3 The spectral density at different platforms

经功率谱对比分析可知，卫星振动频谱较宽，最宽可以达到1kHz，但是一般在80Hz处功率谱会有明显下降，如图3红色框所示。因此，对成像载荷影响最大的振动主要集中在80Hz以内。要实现高精度的运动估计，根据工程经验，运动测量的频率不能够低于运动频率的5倍，因此对80Hz的抖动进行运动估计，最低需要为400帧/s拍摄速度。高速CCD相机成像尺寸小，曝光时间短，可以满足400帧/s拍摄速度要求，所以可以详细记录主成像相机成像期间卫星的抖动。抖动的轨迹既是连续帧图像间像移估计结果随时间的曲线[15]。最后，利用像移估计结果反作用于遥感图像，即可将其清晰化。

由于国内外现有的星载光学成像遥感器没有 CCD相机与主成像相机同轴同步成像的应用实现，故而无法获得实际的连续帧高速 CCD相机成像图片。本文通过对已有的高分辨率遥感图像进行裁剪，从而获得等效的高速 CCD相机成像图片。通过裁剪同一区域遥感图像不同的偏移来模拟因卫星抖动而造成的像移偏差，最后利用相位相关算法对这些像移偏差进行估计，并评价估计结果准确度。

1 相位相关法像移估计原理

相位相关的实现原理[16]是基于傅里叶变换的平移性质。假设一幅图像f1(x,y)平移后形成另一幅图像f2(x,y)，相对平移量为 (x0,y0)像素，则两幅图像分别进行傅里叶变换后的关系式如式（1）所示

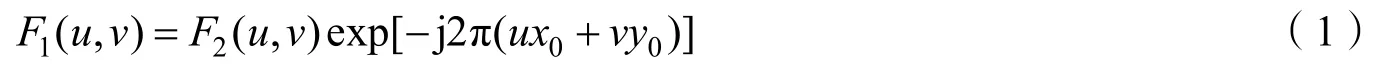
式中F1(u,v)是图像f1(x,y)的傅里叶变换；F2(u,v)是图像f2(x,y)的傅里叶变换。

式（1）说明两幅图像变换到频域中有相同的幅值，而且相对关系仅与相对平移量有关。两个图像的相位差等于图像归一化互功率谱的相位，如式（2）

式中为F2(u,v)的共轭。

为求出相对平移量 (x0,y0)的具体值，只需在对式（2）进行傅里叶反变换即可，如式（3）

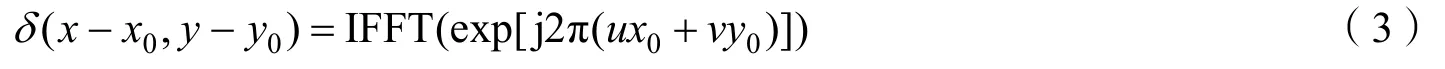
式中 IFFT表示傅里叶反变换；δ表示冲击函数，冲激函数只有在零点才有值，其他点均为零。即当(x,y)的值为 (x0,y0)时该函数才有值，也是冲击函数的最大值。

由式（3）可以看出，互功率谱的傅里叶反变换恰好为平移点 (x0,y0)的冲击函数，由此可以得到图片运动的估计值。

2 相位相关法测试精度分析

以局部城市遥感图片为例，设定偏移大小为（5，4.6）像素。截取原始实际地面城市区域局部图片（256像素×256像素）、CCD成像图片、CCD成像偏移图片分别如图4所示。图4中（a）表示原始图像，（b）表示（a）分离出的图像，（c）表示（b）平移后的图像，（d）是（b）与（c）做相位相关算法后的结果。（d）图Z轴为冲击函数值（无单位）。

为了测试相位相关法的稳像精度，设置如下测试条件。

1）分别选取大小为5 000像素×5 000像素，分辨率为0.5m的城市区域图片做为实际地面参考图像。

2）相位相关算法理论能够准确识别的相对运动分辨率为 0.1个像素[17]。为了使CCD图片拥有0.1像素分辨率的图像信息，截取地面参考图片的大小为2 560像素×2 560像素，在进行10倍的缩小处理，处理方式是每10个×10个参考图片的像素值的和取平均作为CCD图片的像素点值[18]。

3）由于相位相关算法求出两个图像的相对平移量为 (x0,y0)是整数像素值[19]。在图片平移并非整数像素时，虽然 (x0,y0)坐标处的值仍然为冲击函数的最大值，但已经不是唯一有值的点，它周围的坐标也有值，并且形成比较突出的圆锥形，如图4（d）。这表明两个图片的互功率谱能量主要集中在这个锥形上面，只要截取代表这个锥形的坐标值并做平均加权处理，即可得到一个非整数的相对平移量。所以这里截取以 (x0,y0)为中心的相邻区域的一些像素值做平均处理，分别采取 5像素×5像素的矩形图像灰度值拟合，3像素×3像素的矩形图像灰度值拟合，质心拟合，过 (x0,y0)的3点连线像素灰度值拟合方式[20]，求得实际图片的亚像素级偏移量，并评估不同拟合方式的估计精度。

4）因CCD成像速度与图片大小为反比，为达到400帧/s的成像速度，用于稳像的CCD图片的大小最大为256像素×256像素[21]，同时测试图片大小为128像素×128像素、64像素×64像素、32像素×32像素。

5）CCD成像相机X轴方向和Y轴方向的平移范围均为-5～+5个像素，即需要实际地面参考图片平移-50～+50个像素。

图4 使用相位相关法进行像移估计流程举例Fig.4 An example using the phase correlation method in image motion estimation

由图4可以看出，最高脉冲峰的坐标在（50, 90），求得5像素×5像素图像灰度值拟合后得到的平移坐标为（55.0024, 94.6476）。因为此算法用Matlab软件实现，已经将零频率得到的坐标移到图4中心，需要减去平移量，得到的最终平移坐标为（5.0024，4.6476）像素，相对误差为（0.002，0.0476）个像素。

由于CCD相机图片大小的限制，仅截取了参考遥感图片的一小部分作为相位相关算法的原始图像。为了方便得到不同的 CCD图像大小、不同的图像偏移量、不同的图像灰度值拟合方式对算法精度的影响，使用Matlab制作了测试软件，如图5所示。

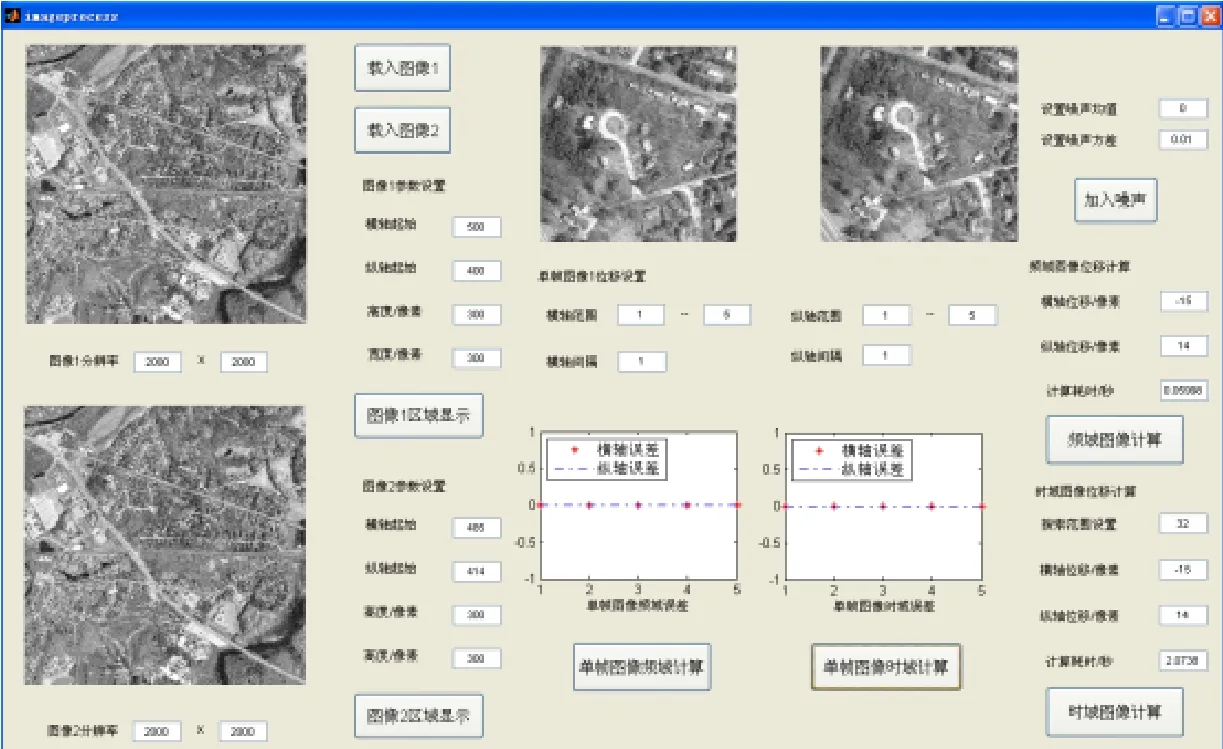
图5 像移估计算法精度分析软件Fig.5 The precision analysis software of the image motion estimation algorithm

当载入参考遥感图片后，使用测试软件截取参考图片的某一部分，指定该部分的大小与需要偏移的像素值，生成原始CCD图片与偏移后的CCD图像，就可以进行像移估计了。

首先使用测试软件测试不同冲击函数拟合方式对像移估计的影响，将城市区域图片进行分块处理，按2 560像素×2 560像素分割成256个不同区域的图片，并将这些图片分别作为原始图片。按上述5条测试条件进行相位相关算法的像移估计的精度分析。将分析结果进行统计，如表1所示。

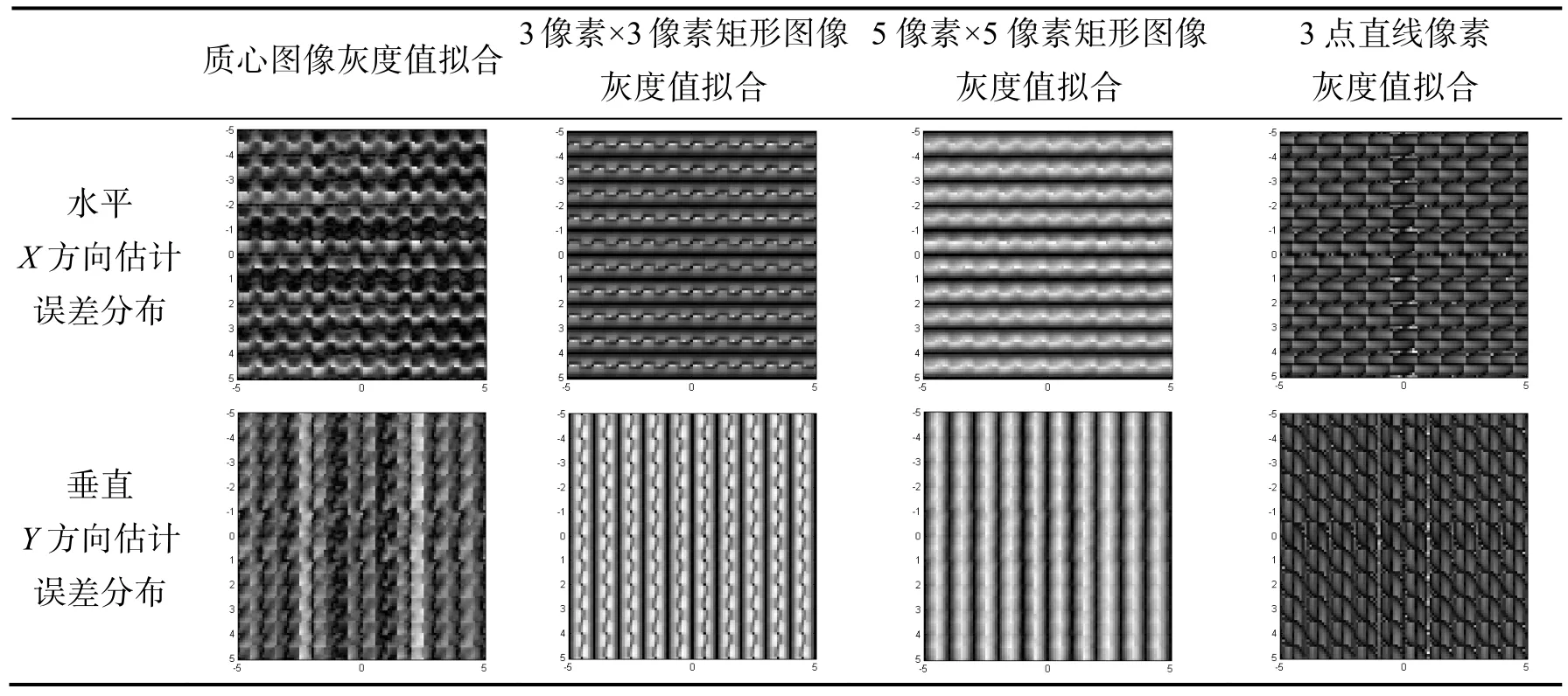
表1 不同拟合算法精度分布Tab.1 The accuracy distribution of different fitting algorithms 单位：像素

原始图像与平移后图像，在水平与垂直方向的平移设定为最大±5个像素的前提下，水平与垂直方向的平移大小以 0.1像素分辨率任意组合的情况下，以图像明暗的方式分别列出每种组合对应的估计误差大小。以表1中第一个小图为例，图中任意点表示的是该点对应的水平和垂直坐标值下，水平方向的误差估计值。误差越小，图像点越暗；误差越大，图像点越亮。对误差值大小进行归纳总结，如表2所示。

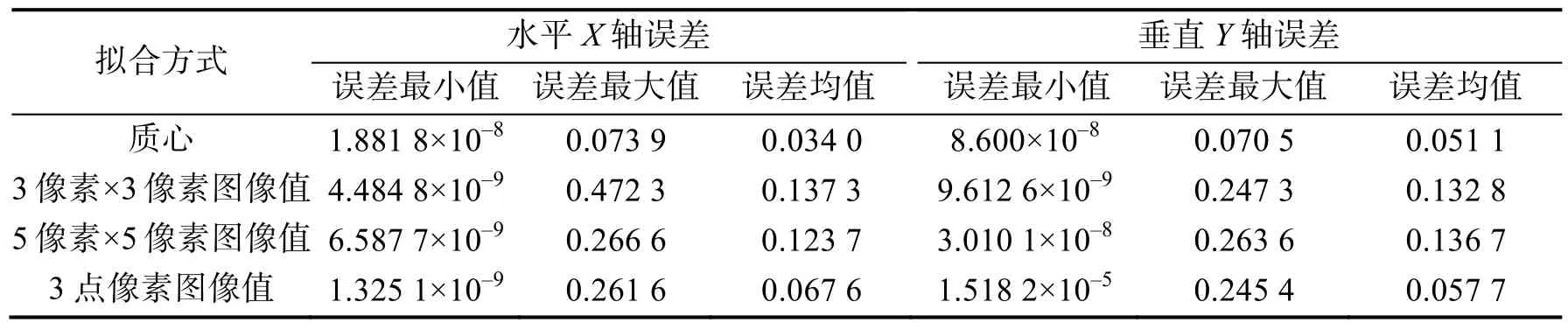
表2 相位相关算法误差综合分析Tab.2 Comprehensive error analysis of the phase correlation algorithm 单位：像素

由表2可以看出，最小误差近似为0，出现在CCD连续帧图像相对平移量为（0，0）坐标。由表1得出，最大误差均出现在0.5个像素整数倍平移位置，具体坐标与图像本身有关。

表3 最优运动误差估计Tab.3 Maximum motion error estimation 单位：像素

表3进一步对表2的精度分布进行了总结。得出使用相位相关算法，结合质心拟合计算做亚像素的精确拟合，能获得最优像移估计结果。

在固定的成像帧频，图像越小，计算量越小，所以如果能够用更小的图片达到相同的效果，则将大大地减少硬件压力。

为了充分验证相关算法对不同图像大小进行像移估计的准确度，将城市区域图片进行分块处理，分别按320像素×320像素、640像素×640像素、1 280像素×1 280像素和2 560像素×2 560像素分割成256个不同区域的图片，并将这些图片分别作为原始图像，进行像移估计的精度分析。使用质心拟合方式作为像移估计拟合方式，按成像大小将分析结果进行统计，如表4～6所示。

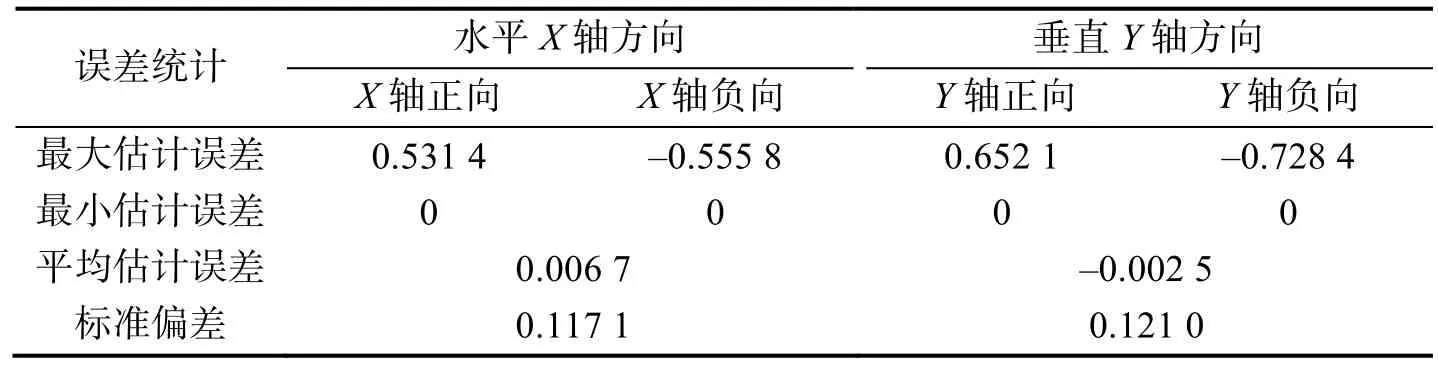
表4 CCD成像大小64像素×64像素的相位相关算法精度分析Tab.4 Accuracy analysis of the phase correlation algorithm for a CCD image with 64 pixels×64 pixels 单位：像素

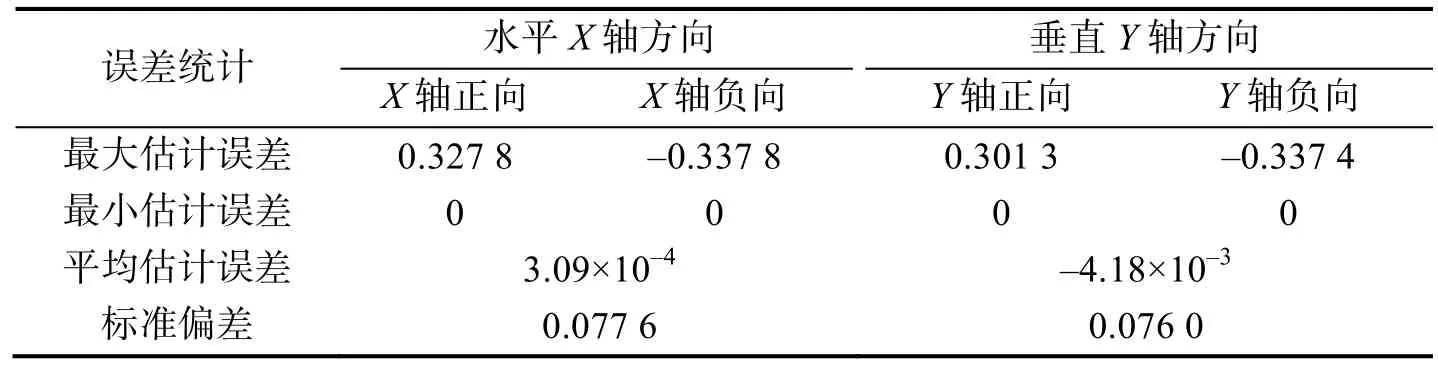
表5 CCD成像大小128像素×128像素的相位相关算法精度分析Tab.5 Accuracy analysis of the phase correlation algorithm for a CCD image with 128 pixels×128 pixels 单位：像素

表6 CCD成像大小256像素×256像素的相位相关算法精度分析Tab.6 Accuracy analysis of the phase correlation algorithm for a CCD image with 256 pixels×256 pixels 单位：像素

由表4、5、6可以看出，最小误差均为0，其出现点为成像图片和偏移图片重合点位置。最大误差均出现在 0.5个像素整数倍平移位置，具体坐标与图像本身有关。成像算法的最大误差值与成像图像大小成反比，大约按 1.5倍关系递减，这说明如果需要较高的像移估计精度，则需采用更大的成像图像，但耗时更多，需要折中处理。

在使用CCD成像32像素×32像素图片进行像移估计时，有可能导致相关算法失效，即当平移图像平移到某个点或某片区域时，利用相关算法计算出的误差已经为多个像素。具体失效区域与图片的具体内容相关。对所有的分割图片进行统计，假定像素偏移误差大于0.5个像素则为失效，失效概率为92%；若假定像素偏移误差大于1个像素则为失效，失效概率为86%。这说明针对32×32像素图片进行像移估计，失效概率过高，该方法无法使用。失效形式如图6所示两种情况。

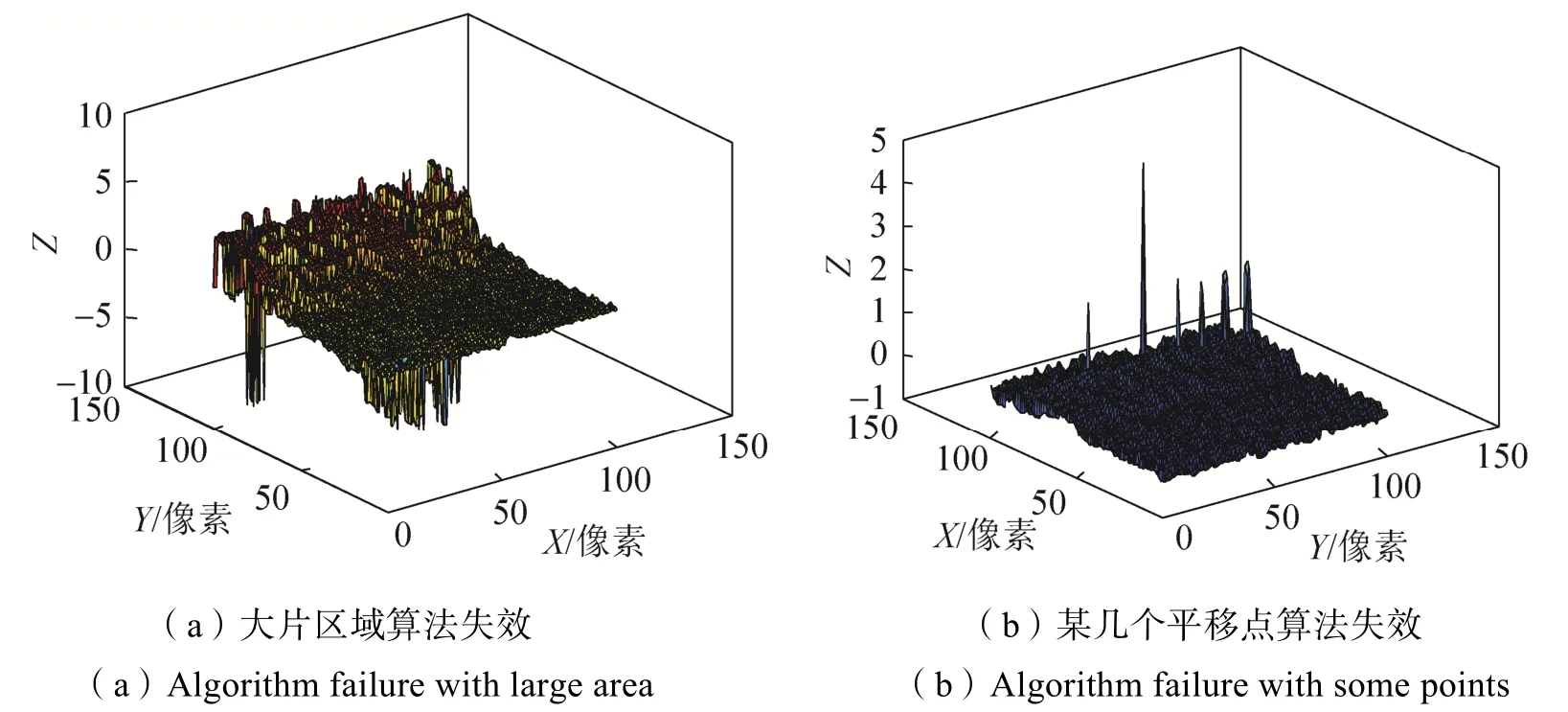
图6 32像素×32像素CCD成像图片像移估计算法失效举例Fig.6 A failure example of the image motion estimation algorithm for a CCD image with 32 pixels×32 pixels

图6与表1表达的物理意义是一样的，不同点在于表 1每个小图的值是随X和Y的值连续变化，而图6的值出现了突变，且突变点是没有规律的，分别为图6（a）的大面积突变失效和图6（b）的某几个点失效，如果实际像移点出现在失效点，像移估计将出现极大误差，甚至超过了真实像移值本身。这说明当CCD成像大小为32像素×32像素时，由于图像信息采集量不足，在某些情况下使用相位相关算法采集到的互功率谱的傅里叶反变换峰值不再特别独立[22]。互功率谱的傅里叶反变换图像如图7所示。

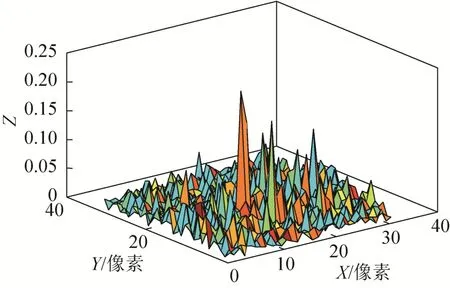
图7 32像素×32像素CCD成像图像的互功率谱的傅里叶反变换图片Fig.7 The inverse fourier transform image of cross power spectrum of the CCD image with 32 pixels×32 pixels

由图7可以看出，极大值不唯一，虽然最大值唯一，但算法可能无法提取图像的最大值，而错把临近的极大值作为最大值对应的坐标输出。这使得相位相关算法失效，获得的值也是错值。

3 结束语

本文主要分析了对高速 CCD相机对地成像的图片使用相位相关算法提取像移信息，复原遥感图像所能达到的精度与算法使用条件。分析结果表明，在满足 0.1像素分辨率的前提下，更大的图像、整数倍像素偏移、使用质心拟合方式可获得更好的估计精度。当图片小到32像素×32像素时，有可能引起该方法失效。

虽然是使用仿真的方式对相位相关算法的像移估计精度进行的分析，但使用的遥感图像等数据源均来自于实际遥感成像图像，因此仿真算法也可直接使用于真实系统中。本研究也为未来实际的在轨应用提供了实验依据。

本研究没有考虑到实际测量噪声对相位相关算法的影响[23]，后续将开展不同信噪比对算法估计精度影响的分析。