射伞火箭开伞过程动力学仿真与分析

刘涛 许望晶 滕海山 张章

（北京空间机电研究所，北京 100094）

0 引言

降落伞开伞环节是飞行器回收的关键环节，传统回收系统一般使用弹射器或弹伞筒等弹射类火工装置作为第一级降落伞的开伞执行机构[1]。这类装置开伞时会对安装基座产生很大的弹射后坐力，给承载结构设计带来很多问题。射伞火箭开伞与弹射开伞最大不同在于：射伞火箭点火后就与机体分离，其火药持续燃烧一小段时间（燃烧时间从数百毫秒至数秒不等），这期间使降落伞伞包（以下简称：伞包）相对于回收物从零速加速远离，伞包的动量增量由射伞火箭通过连接带拖拽提供，因而对机体几乎没有后坐力；而弹射开伞是火药内能瞬间释放（燃烧时间从数毫秒至数十毫秒不等），转化为伞包的初速度，其伞包动量的增量来源于弹射器，而弹射器固定安装在机体上，需要机体安装部位具有很强的承载能力。由于射伞火箭的低后坐力特性，在某些场合是弹射器无法替代的开伞执行机构，因此有必要对射伞火箭开伞过程进行分析及研究。

降落伞开伞过程是回收专业研究的热点之一，文献[2]分析了再入返回舱尾流对弹射开伞过程的影响，采用了重叠网格技术，构建了钝头体尾部弹射开伞的气动-动力学耦合仿真模型，相比传统的先获取气动数据再进行动力学计算的分析方案具有精度高，灵活性好的优点；文献[3-4]分析了探月工程中弹盖拉伞的动力学过程；文献[5-6]对载人飞船中弹盖拉伞的过程进行了动力学建模和分析，这两项专项工程均采用了弹射舱盖拉出降落伞的方案，表明通过具有一定初速度，无动力的舱盖拉直降落伞的技术具有较好的成熟度；文献[7-9]分别介绍仿真了火星探测中弹伞筒开伞形式，并对存在攻角弹伞过程的“绳帆”现象进行了分析计算，系统地描述和分析了以弹伞筒形式展开降落伞的动力学过程；文献[10]把弹射过程伞包近似成可压缩弹性体，对弹射速度需求和伞包受力进行了分析；文献[11-12]中给出了常见形式下弹射开伞所需求的弹射速度计算方法；文献[13-14]给出弹射开伞过程拉出降落伞的参考模型。这些研究情况表明，对于弹射开伞，已有多种成型数学模型可以参考。

对于使用射伞火箭开伞，文献[15]提出了用于降落伞快速开伞的射伞火箭专利，但分析其开伞过程的文献很少，设计参考资料还存在空白。本文以正在平飞的飞行器回收开伞过程为背景，建立了射伞火箭拉动伞包过程的动力学模型，并对相关参数对过程的影响进行了计算分析，为此类装置系统设计时面临的指标合理分配问题提供了解决思路。

1 系统组成及说明

射伞火箭工作过程如图1所示。假定回收启动前，飞行器匀速平飞，射伞火箭和伞包之间由连接带连接，回收系统启动后，射伞火箭点火，连接带拉直后拉动伞包快速远离飞行器，过程中逐步拉直吊带、伞绳和伞衣，伞衣完全拉出后，射伞火箭牵引空伞包与系统分离。

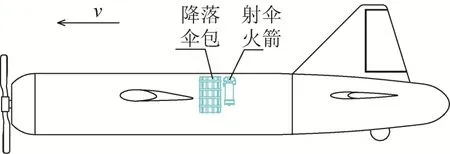
图1 射伞火箭工作前状态Fig.1 Status of propelling rocket before operation

射伞火箭拉动伞包过程如图2所示。

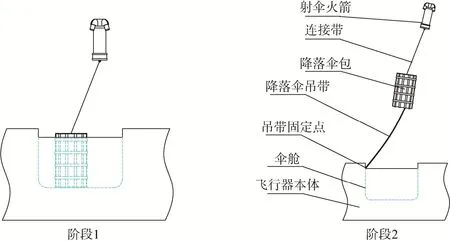
图2 射伞火箭工作过程Fig.2 Working process of propelling rocket

2 系统动力学模型

2.1 系统模型

一般来说射伞火箭开伞过程时间很短，对飞行器速度姿态干扰也很小，借鉴文献[16]的简化处理方法，认为开伞过程近似为平面内的运动，这一过程飞行器以速度v匀速平飞。射伞火箭工作过程受力如图3所示。

图3 系统受力示意Fig.3 Diagram of System force analysis

主要符号涵义见表1。

图中的A1点为射伞火箭推力的理论作用点（考虑稳定性，射伞火箭一般喷口前置），A2点为降落伞拉出力作用点，B1为连接带拉力对射伞火箭作用点，B2为连接带拉力对伞包作用点，C1和C2分别为射伞火箭和伞包的质心位置；随着射伞火箭燃烧和降落伞拉出，A2、C1、C2点相对于各自坐标系为动点，同时射伞火箭和降落伞的质量及转动惯量也是变化参量。

此外建模过程做的一般性的简化如下：

1）平面大地，风速为零；

2）忽略高度引起的重力加速度变化[17]；

3）射伞火箭、伞包等按照刚性回转体处理，射伞火箭和伞包视为纯阻力体，气流载荷过型心；

4）伞绳拉出过程不考虑“绳帆效应”的影响[18]。

由于飞行器在射伞火箭工作过程中速度姿态变化可忽略，因此惯性系可固连在飞行器本体上，不失一般性，把惯性坐标系O-X-Y的原点设置在降落伞吊带固定点，惯性系Y轴正方向朝上，X轴正向与飞行速度方向相反。射伞火箭和伞包工作过程中都有质量重心变化，忽略射伞火箭质量和速度变化对喷射推力的影响，把坐标系原点都设置在型心，Y轴沿轴线，正方向朝上。

对射伞火箭和伞包在惯性系中应用动量定理：

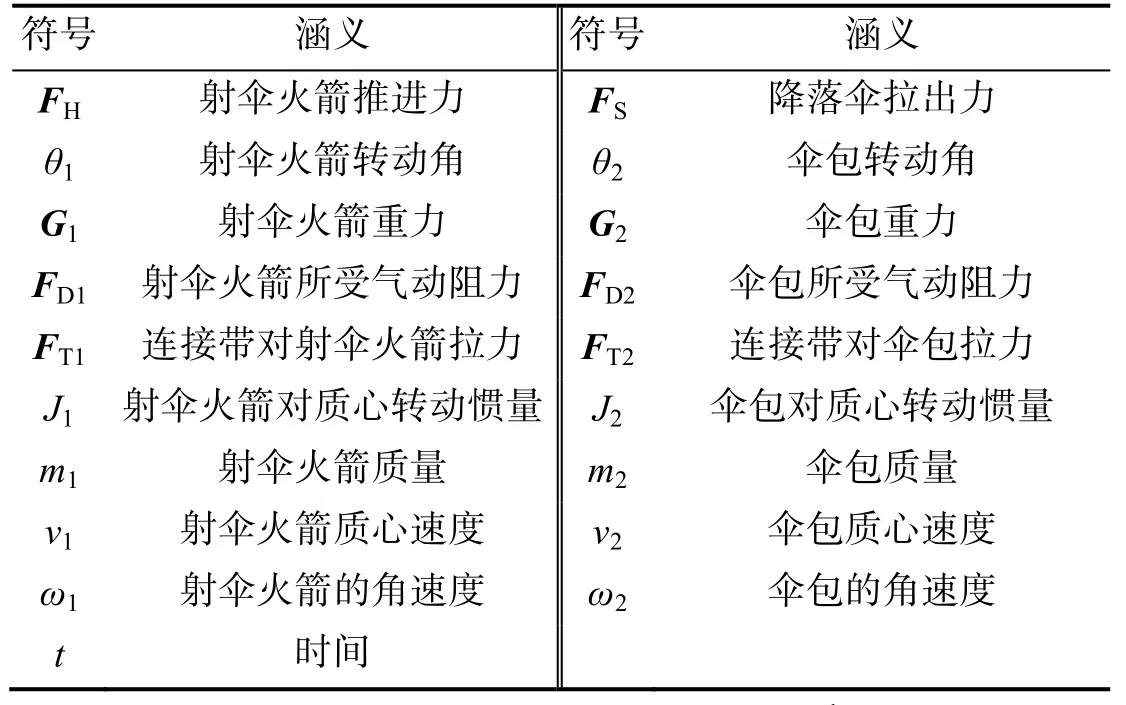
表1 主要符号涵义表Tab.1 List of symbols

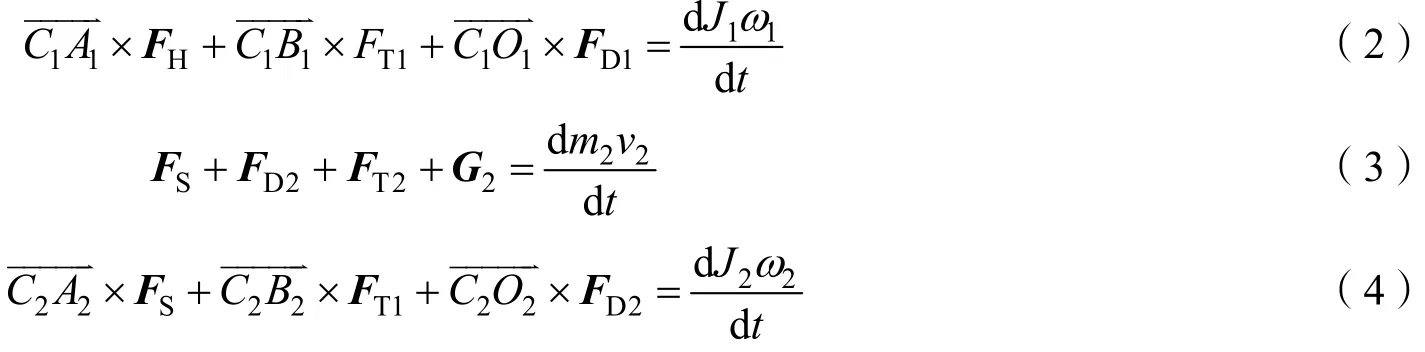
2.2 射伞火箭

（1）质量特性

依据射伞火箭的产品特性，参考文献[19]的对火箭质量特性的处理方法，射伞火箭内火药燃烧匀速，则射伞火箭质量表达式为

按照射伞火箭内火药为圆柱型，单截面燃烧，则其转动惯量随时间近似关系可表示为

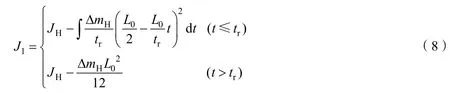
式中mH和JH是射伞火箭初始质量和转动惯量；tr是射伞火箭火药燃烧总时间；ΔmH是燃烧前后质量变化量；L0是火药药柱的初始长度。

（2）推力

射伞火箭火药燃烧过程推力大小可近似为恒值，燃烧完后推力为零。

式中P为射伞火箭火药燃烧过程的平均推力大小。

2.3 连接带

连接带一般由特纺材料制成，具有较高承载能力，一般视为分段阻尼弹簧模型[20]，在其断裂伸长范围内，其拉力计算方法如式（10）

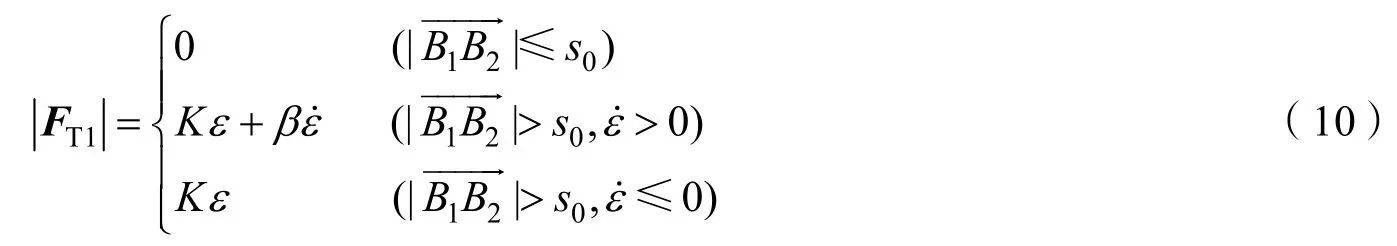
式中ε为连接带伸长率，为连接带伸长率对时间的一阶导数；s0为连接带原长；K为表征连接带弹性的参数，K=断裂强力/断裂伸长率；β是表征阻尼的参数。

2.4 伞包

（1）质量特性

伞包在开伞过程为变质量体，伞包质量变化情况参考文献[21]中的连续拉出模型，近似认为拉出部分降落伞的线密度是关于拉出长度的分段函数，考虑到降落伞在伞包中的包装状态，可认为伞包内部的密度是均匀的，这样就可以得出伞包质量、质心和转动惯量随拉出长度的变化关系，这里不再详述。

（2）包装特性

本文参考了文献[18]对伞包拉出力的分析方法，考虑了降落伞在包伞过程所设置的约束绳的影响，并在其基础上对拉出载荷进行了进一步简化，认为降落伞拉出力由已拉出降落伞重力、摩擦力和约束绳拉断力合成，作用点保持在A1点，方向与A1点至吊带固定点连线一致。

3 不同参数对系统工作过程的影响

开伞过程最关注的是降落伞拉直的快速性和稳定性，与这两项指标相关最紧密的参数为伞包飞离机体的位移和摆动角度，位移能够表征拉出降落伞长度，而摆动角度表征伞包开口朝向，开口偏转到一定程度会发生降落伞或吊带缠绕。工程中允许在降落伞拉出过程中，伞包存在一定的摆动，本章参考文献[22]中的分析项目和分析方法，对这一工作过程可能存在偏差及主要设计参数影响进行了分析，寻求其对拉直快速性和稳定性的影响趋势和程度，作为产品工程实现依据。

表2给出了建模过程中涉及的常量或变量初始值的默认取值，部分仿真项目会调整其中某项参数取值，调整情况在对应的仿真章节中给出。

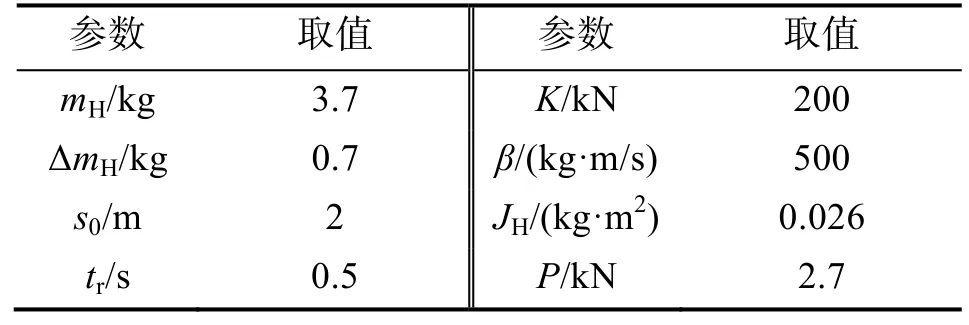
表2 参数取值表Tab.2 Parameter values

3.1 射伞火箭与伞包轴线位置偏差

射伞火箭与伞包同轴安装是有利于降落伞拉出的布局，但受飞行器空间影响，实际射伞火箭和伞包轴线会偏离一定距离，这种情况下，射伞火箭拉直连接带一刻起，即受到连接带侧向力，造成其转向，不利于降落伞拉出，对箭伞轴线不同偏差下伞包运动情况进行分析如图4所示。

图4 箭伞轴线位置偏差的影响分析Fig.4 Influence analysis of axis position deviation between the rocket and parachute bag

图4中，伞包摆角是B1B2连线与伞包轴线的夹角，伞包位移是O2与O之间的距离。从图中可以看到箭伞轴线存在一定偏差时，当射伞火箭拉直连接带后，连接带与伞包轴线和射伞火箭轴线都存在一定角度，箭伞轴线间距越大，这个角度越大，连接带造成伞包和射伞火箭翻滚的分力越大；从仿真结果来看，应优选箭伞同轴安装（间距0m），如无法同心安装应尽量减小箭伞轴线间距。

3.2 射伞火箭推力线偏差

射伞火箭受制造偏差影响，可能推力线比理论值有偏差，取初始箭伞间距为0m，对推力线存在偏差情况下射伞火箭工作过程计算如图5所示。

图5 射伞火箭推力线偏差的影响分析Fig.5 Influence analysis of thrust line deviation of the propelling rocket

由图5结果可知，随着射伞火箭推力线偏差增加，会造成伞包摆角过大，对开伞可靠性影响越大，同时伞包拉出进程也越慢。从仿真结果可以看到，射伞火箭推力线偏差对伞包拉出稳定性影响非常明显，0.15°的偏角就会造成伞包摆角发散，降落伞拉出过程延迟。

3.3 连接带材料刚度

不同连接带材料，断裂伸长率有较大的不同，使得参数K差别很大。选取3种常用的材料（详见表3），设置同样断裂强力和阻尼比进行仿真计算。仿真结果如图6所示。

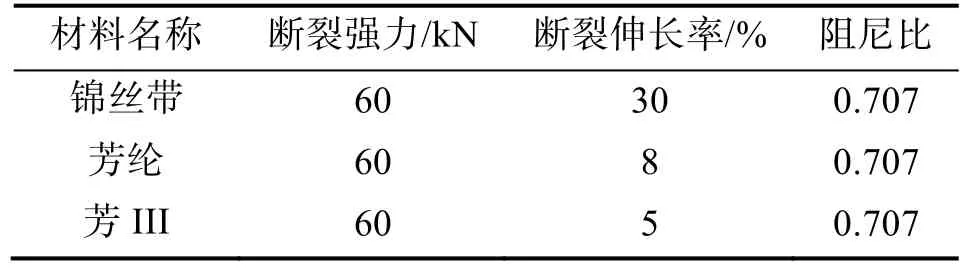
表3 常用连接带材料参数Tab.3 Material parameters of common connecting belt

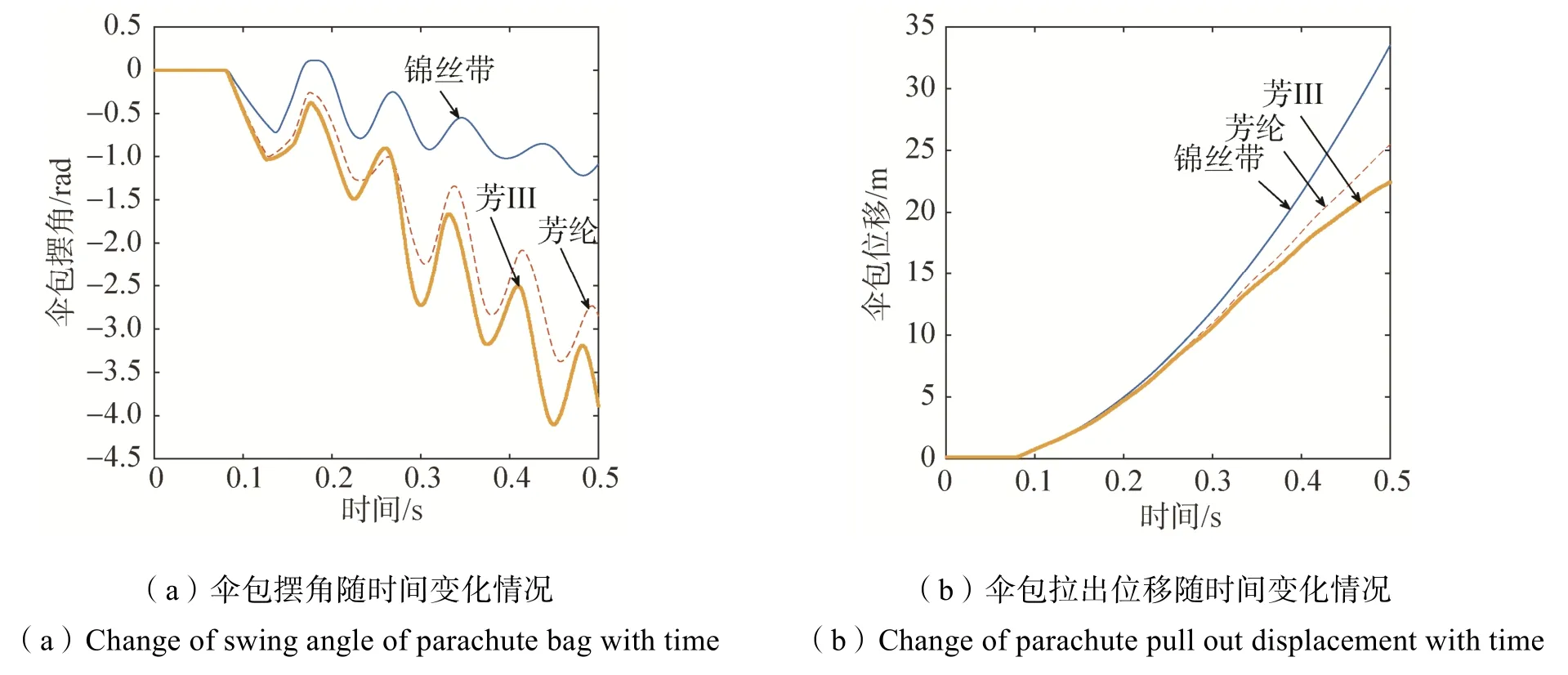
图6 不同连接带材料的影响分析Fig.6 Analysis of the influence of different materials of connecting belt

从图6分析结果来看，刚性较强的芳纶和芳III连接带使伞包摆动程度更为明显，并且伞包分离进程也更为滞后，因此连接带宜选用刚性较弱的材料，对应的是断裂伸长率较大的材料。

3.4 连接带阻尼比

连接带阻尼比的概念由参考文献[23]对二阶震荡系统的描述引出，伞包受拉时，把伞包看作质点，假定其质量为m，伞包运动类似带阻尼的弹簧振子，其运动方程为

对应的特征方程是

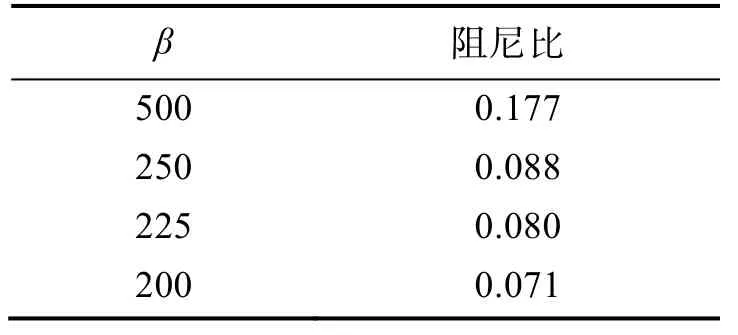
表4 连接带阻尼参数设置Tab.4 Damping parameter of connecting belt

按照弹簧振子的理论，阻尼比ξ＞1、ξ=1、0＜ξ＜1、ξ=0分别称为过阻尼、临界阻尼、欠阻尼和无阻尼，均对应不同的运动特性。一般来说，特纺材料制成的连接带ξ不超过 1，系统具有欠阻尼的特性。取初始箭伞间距为0.2m，选取了表4中不同β对系统工作过程进行了计算。

伞包摆角和伞包位移计算结果如图7所示。

从图7仿真结果来看，阻尼比ξ较大时伞包运动较为稳定，过小则造成伞包摆动角度振幅很大，这在工程设计上是不允许的。在选择连接带材料前，应对阻尼特性进行测定，避免因该项参数存在较大偏差造成设计结果反复。

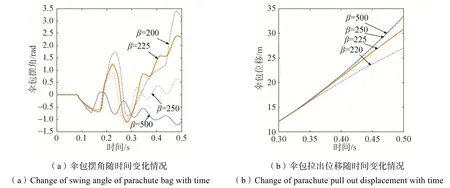
图7 连接带阻尼比的影响分析Fig.7 Influence analysis of damping ratio of connecting belt

3.5 连接带长度

连接带长度直接影响连接带拉直时与伞包轴线的夹角，射伞火箭对伞包的速度差，连接带拉直时，也影响连接带自身的储能能力，取初始箭伞间距为0.2m，保持连接带的阻尼比不变，对不同的连接带长度计算结果如图8所示。

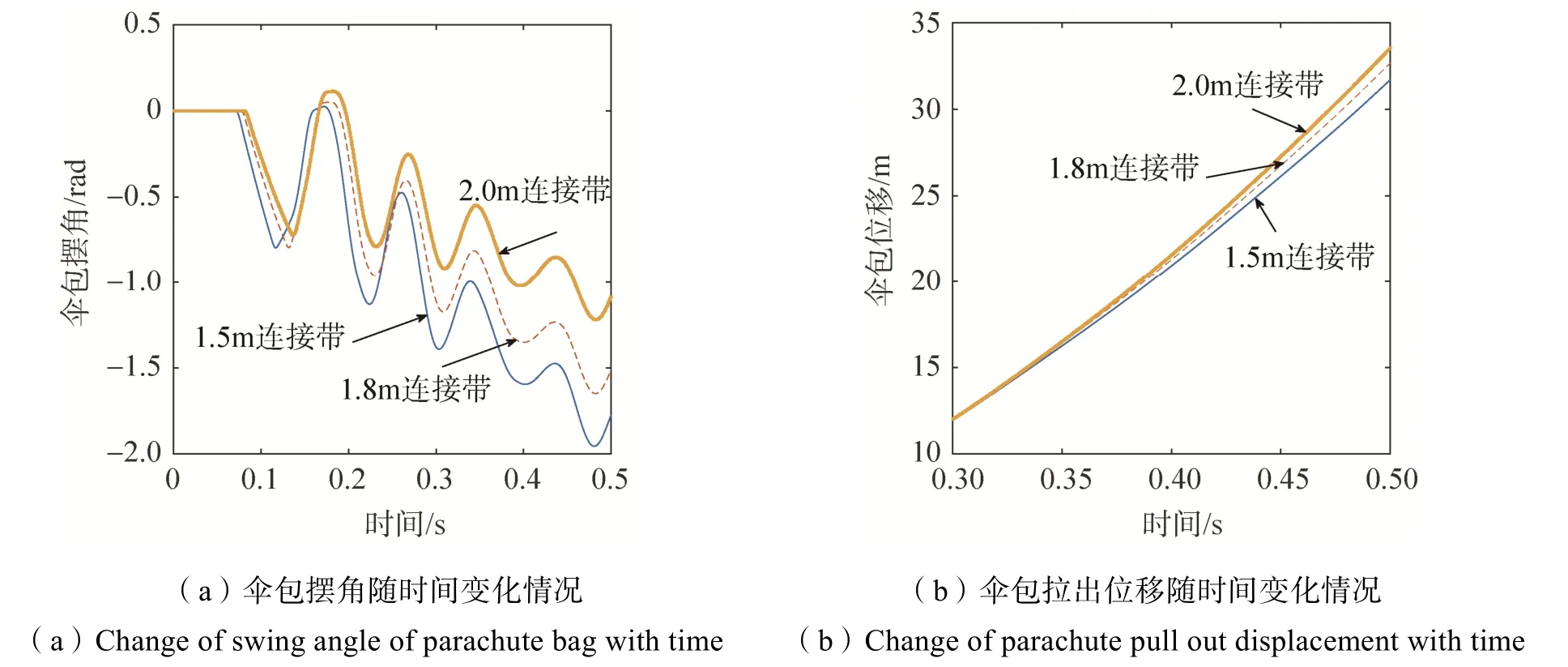
图8 连接带长度的影响分析Fig.8 Analysis of the influence of the length of the connecting belt

从仿真结果来看，连接带越长，伞包拉出过程越平稳，继续增加连接带长度至 2.5m、3m（受图片空间所限，这部分内容没有显示在图中），连接带增长对伞包平稳性改进不再明显，从这一特点来看，连接带长度不同引起的拉直时与伞包轴线的夹角不同，是对系统运动影响最大的因素。

4 结束语

本文对射伞火箭倒拉伞包开伞过程进行了动力学建模，依据分析可知，射伞火箭推力线的偏差和箭伞安装不同轴偏差均会造成伞包摆动，进而给开伞带来不利影响；同时选择合理的连接带参数有利于控制射伞火箭工作过程伞包摆动的发散。分析结果对产品设计有以下借鉴意义：

1）应严格控制射伞火箭的推力线偏差；

2）在无法实现箭伞同轴安装时，可以通过适当加长连接带，来减小开伞过程伞包摆动；

3）在连接带强度满足要求前提下，宜选用断裂伸长率较大的材料；

4）应设计试验测定连接带的阻尼比，对连接带阻尼比偏低的情况，可采取箭伞同轴设计，或设置撕裂带等增加阻尼的结构。

本文研究方法和内容对设计射伞火箭开伞装置具有较好的针对性和参考价值。但文中对整个系统的建模仍有较多的简化，如：射伞火箭气动力只考虑了阻力，平面刚体模型无法模拟某些飞行器开伞时存在三轴角度、角速度的状态。在下一步研究中，应考虑回收过程中存在的多自由度空间运动时伞包的分离可靠性问题。