散客乡村旅游路径选择多目标模型研究

戈冬梅，赖志柱，陈群利，彭水亮

（1.贵州工程应用技术学院生态工程学院，贵州 毕节 551700；2.华东师范大学地理信息科学教育部重点实验室，上海 200241）

一、引言

随着我国居民生活水平的提高和消费观念的改变，居民选择乡村旅游的行为和现象呈现持续发展的趋势。乡村旅游线路的设计是乡村旅游极其重要的一个环节，一条好的乡村旅游线路可以很好地对乡村旅游资源和特色服务项目进行整合，从而推动乡村旅游的良序健康发展。楚义芳初步研究了旅游线路设计的理论框架及国内旅游线路设计应重视的若干问题[1]；周红军探讨了乡村旅游线路设计中应重点考虑的游客乡村体验需求和短程短时间等五个原则[2]；饶华清通过分析澳大利亚徒步旅游线路特点给出了对我国的几点启示[3]；李强等分析了山西旅游线路设计中的不足并提出了线路设计优化的整合及提升等具体思路[4]；殷晓晶等分析了基于旅游者需求的自助旅游线路设计的特点并提出了线路设计的流程图[5]；刘丽梅等[6]通过分析内蒙古杭锦旗乡村旅游的现状及存在的问题，提出了基于生态旅游理念下该地乡村旅游发展的若干原则；陈翔[7]通过对四川民族地区进行区位分析并进行旅游归类，得出四川民族地区乡村旅游可分为原野型和城郊型两种乡村旅游模式。这些研究多探讨旅游线路设计原则或特定区域的乡村旅游线路的特征分析及对策研究。方冬云[8]建立了近似旅游线路的图论模型并采用最邻近插入法和分支定界法求解；刘峙麟等[9]基于层次分析法和图论模型优化旅游线路并与已有线路作对比；王宁[10]采用基于模糊数学的综合评判方法研究最优旅游线路的选择，但指标权重及效用函数却不好确定；徐锋等[11]将旅游路线规划类比化简为TSP回路问题并提出一种改进的蚁群算法求解；孟爱国等[12]利用遗传算法求解游遍所有景点的最短路径模型。这些研究主要是将旅游线路问题转化为图论模型或TSP问题，最后都汇总为最短路问题进行求解。

上述这些研究都没有考虑旅游线路设计中旅游者本身的感受。由于旅游者对旅游线路的选择具有多方面的要求，如旅游者希望花费在旅游路途中的时间越短越好、希望乘坐的交通工具越舒适越好、希望旅游途中能欣赏的风景越多越好等。特别地，对于旅游散客而言，由于各自的经济基础、旅游费用预算、旅游时间限制以及享受旅游的需求不同，还需要考虑旅游费用、旅游时间甚至是散客对旅游交通工具的满意程度等问题。通常，当游客确定了旅游目的地以后，通常会先设计自助旅游的线路。在当前庞大的网络信息、各种游玩攻略、导航软件、各类APP的助力下，很容易预先确定自主旅游需要经过的一些旅游中转位置（也称中间节点或中间城市）。当确定了旅游线路经过的中间节点后，旅游费用与时间主要与旅游时选择的交通工具有关，而散客对旅游线路及线路上交通工具的选择更是具有不同的满意程度。不同的散客对不同的交通工具会有不同的选择，从而导致散客旅游费用、旅行时间及旅游满足程度各不相同，因此有必要考察散客对旅游线路乘车路径的选择问题。

此外，散客对旅游线路乘车路径的选择可以看作是物流作业中多式联运问题在旅游方面的变形和应用，这是因为物流多式联运涉及的多种运输方式可以对应于散客旅游的多种交通工具。但本文研究与物流多式联运的最大不同之处在于货物运输与散客旅游乘车的区别，即物流多式联运是针对货物，而散客旅游乘车是针对人，而人与货物最大的区别在于是否考虑舒适度、满意度或安全度上。为此，我们借鉴物流多式联运关于路径优化决策问题的研究，将多目标多式联运问题的研究思路和解决方案[13-18]应用于散客旅游乘车路径选择上。

为此，本文研究散客在乡村旅游中的乘车路径选择问题，考察旅行途中交通工具的费用、时间等要求，结合旅游途中换乘交通工具的费用及时间开销，建立散客乡村旅游乘车路径选择的多目标数学模型。当旅游中途需经过的地方较多时，求解多目标数学模型的传统方法速度较慢，为此专门构建求解该模型的离散粒子群算法，并通过实例进行验证研究，扩展乡村旅游路线的研究方向。

二、问题描述及模型

假设有一批散客想到某一乡村旅游景点旅游，出发地到旅游地需要经过若干中转地，为叙述方便，统称出发点、旅游目的地、中转地为节点，则问题可以描述为：一批散客从起始节点出发，中间经过若干节点，最终到达旅游目的地节点，相邻节点间有若干的交通工具可供选择，相邻节点间的每一种交通工具有不同的运输费用和运输时间，且从一种交通工具转换到另一种交通工具时可能需要一定的时间和费用，现在需要为这批散客在所有节点之间选择合适的交通工具以便在尽可能少的费用、时间约束及尽可能大的满意度下到达旅游目的地。

为便于模型建立，作如下假设：

假设1由于旅游散客之间通常都比较熟悉，除了家人外，也可能是关系要好的朋友或同学等，因此假设该批散客在本次旅游期间自始至终都是同进同退，不分开；

假设2当旅游者人数较多时，通常会选择旅行社以减少旅游费用以享受旅游折扣的优惠。只有旅游者人数较少，在旅行社无法享受旅游费用优惠，而开展自主旅游却能节省费用以及享受旅游自主性，此时通常的旅游交通工具都能满足该批旅游者的需求。为此，任意节点间可供选择的交通工具均足够装载该批散客，即散客数量不超过任一种交通工具的运量；

假设3由于散客在路途中间对环境不熟悉且转换交通工具匮乏，为此假设散客只在节点处选择交通工具，不在节点之间（子路径）选择交通工具；

假设4根据假设1，旅游散客之间通常比较熟悉，习惯于同进同退，所选择的旅游子路径和交通工具通常具有一致性。为此，假设散客在任意两个节点间只选择同一种交通工具和同一条旅游子路径；

假设5虽然每个人对旅游环境、旅游路径、旅游交通工具及费用等有自己的感受，但这种感受可以统一为一个群体的总体感受。为此假设散客在各条子路径上的满意度仅与乘坐交通工具的舒适度有关，不考虑子路径上风景观赏及乘车费用或时间开销等的满意度。

在上述假设及符号表示下，建立散客乡村旅游路径选择的多目标模型如下

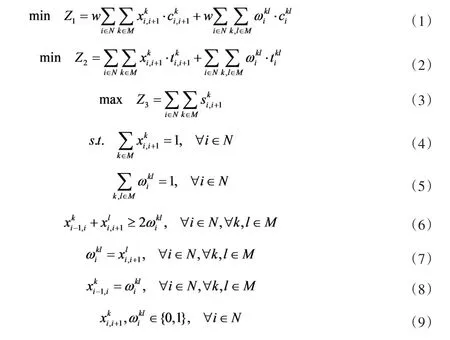
三、算法设计及模型求解

（一）多目标的处理

由于本文建立的散客乡村旅游路径选择模型包含三个目标，而目前通用的NSGA-II等多目标智能算法对双目标模型的求解比较有效，针对三个目标的算法需要重新设计。为此，我们首先引入优势排序数[18]的概念处理三个目标，并依据优势排序数构建适应度函数。

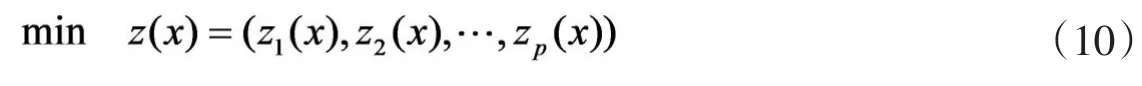
（二）基于优势排序数的多目标离散粒子群算法

粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的演化计算方法，最早由Kennedy和Eberhart于1995年提出[19]，源于对鸟群捕食的行为研究。粒子群算法利用群体中的粒子个体对信息的共享从而使得整个群体在问题求解空间中有序高效地演化并获得问题最优解，具体地说，就是群体中每个粒子都通过跟踪粒子本身历史最优和群体历史最优来更新自己的位置，通过迭代从而寻到问题最优解。PSO的优势在于简单易于实现并无需太多的参数调整，目前已成功应用于多个优化领域中[20-22]，显示出该算法具有较强的鲁棒性和广泛的应用前景。

1.问题的编码

当确定旅游时需经过的节点后，问题求解仅需确定旅游时各子路径（节点与节点间）上的交通工具。假设每条子路径上有种可能的交通工具，先将各交通工具编号为，若某两节点间没有某交通工具，则将此处的乘车费用和时间均设置成很大的数。在此基础上，采用字符编码方式，每一码位表示旅游过程中所经过的一条子路径，码位上的值表示在该子路径上乘车时选择的交通工具。例如，若散客旅游时从起点O到目的地D之间顺序经过3个节点A、B、C，用长度为4的一组数字表示某一交通工具选择方案，如编码，表示从O到A选择交通工具3，从A到B选择交通工具2，从B到C选择交通工具1，从C到D选择交通工具1，此时运输路径中节点A、B处均发生了交通工具转换。

2.粒子的更新

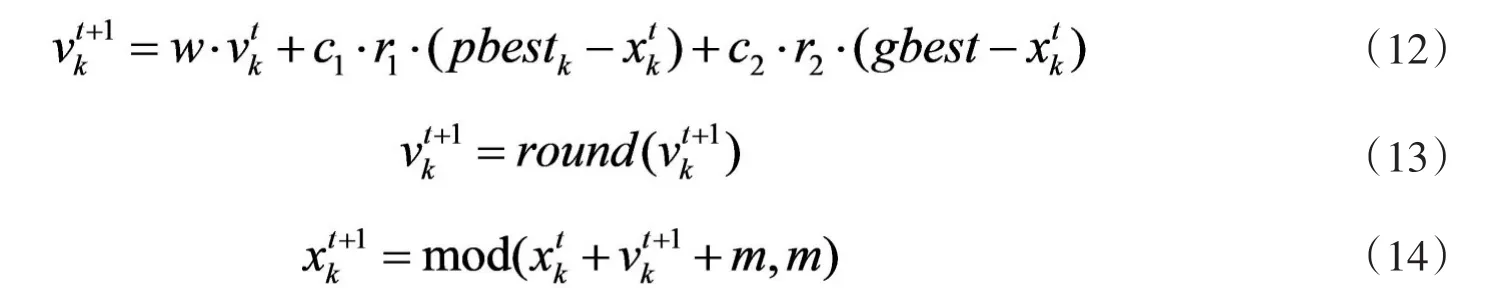
3.算法步骤

步骤1输入问题的数据（乘车费用、乘车时间、满意度矩阵、中转费用及中转时间等）及粒子群算法的参数（群体粒子数目pNum、最大迭代数MaxGen、惯性权重、个体学习因子及社会学习因子）；

步骤2初始化粒子群体：随机初始化所有粒子的位置和速度，计算每个粒子的旅游总费用、旅游总时间和总满意度，根据总优势排序数计算其适应度值，初始化每个粒子的历史最优位置；

步骤3寻找当前粒子群体的Pareto最优解集，并将具有最大适应度的粒子作为当前群体的全局最优粒子；

步骤4更新所有粒子的位置和速度，计算对应的旅游总费用、旅游总时间和总满意度；

步骤5计算每个粒子的适应度，更新个体的历史最优位置；

步骤6更新群体的历史最优粒子；

步骤7更新Pareto最优解集；

步骤8若不满足停止条件，转步骤4；否则输出算法所获得群体的历史最优粒子以及Pareto最优解集的信息。

四、案例分析

某省会城市的一批散客想到该省某地级市进行一次乡村旅游，旅游时需顺序经过几个节点才能到达旅游目的地，每个节点处均有多种交通工具（记为A、B、C）供选择。假定散客数量为3，其它数据参见表1与表2。表1数据a∕b∕c中，a表示单位交通费用（元∕人），b表示乘车时间（h），c表示在路段上选择某交通工具的满意度；表2数据中，分子表示各交通工具间的单位中转费用（元∕人），分母表示中转时间（h）。

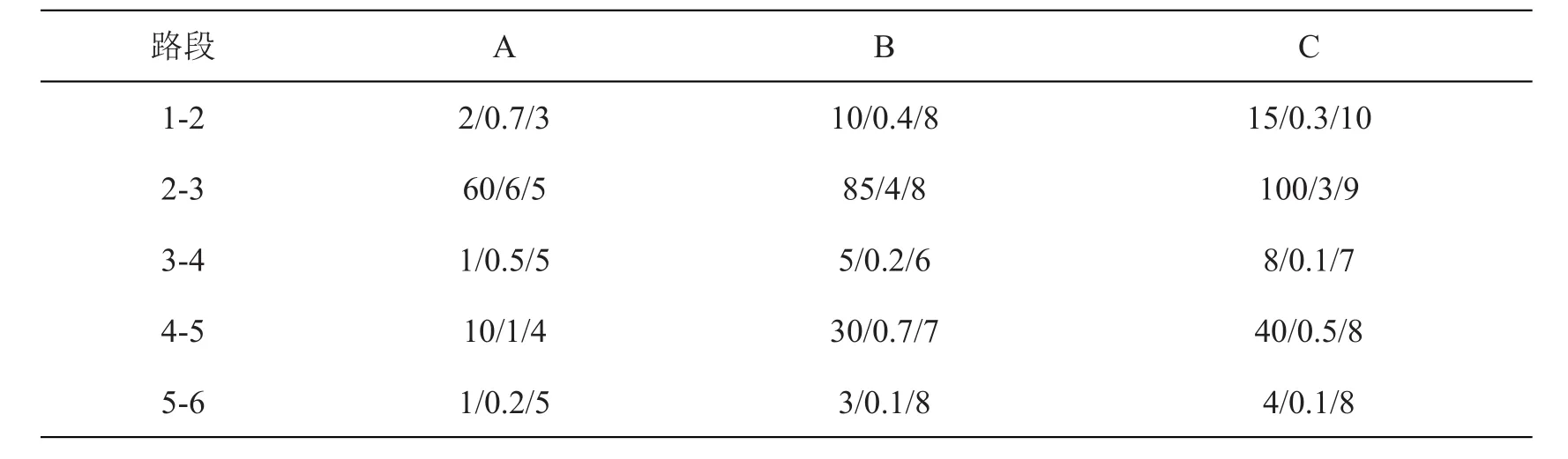
表1 各路段不同交通工具的相关数据

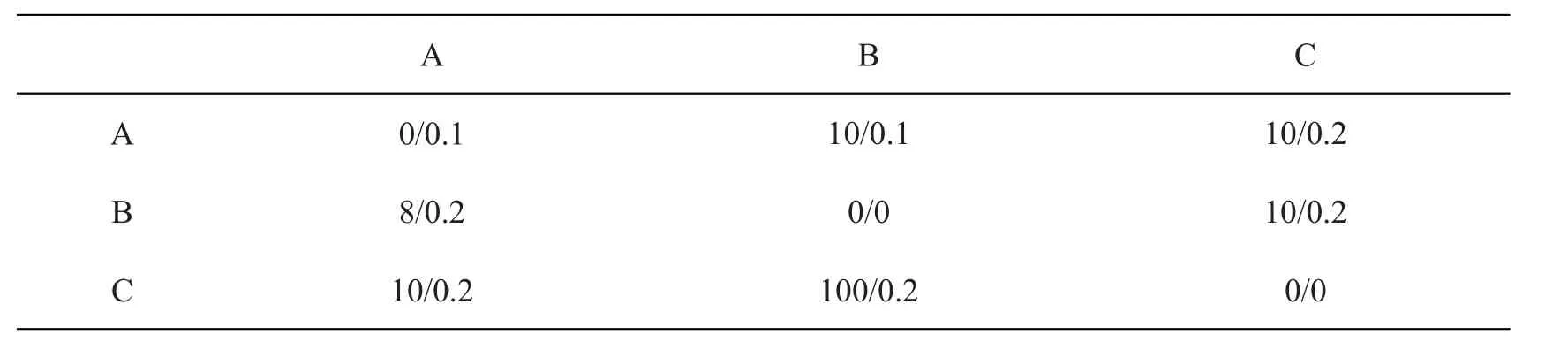
表2 各交通工具间中转费用和时间表

取群体粒子数目pNum=30、最大迭代数MaxGen=200、惯性权重及学习因子，基于MATLAB编制程序求解，本文粒子群算法获得的Pareto最优解结果见表3，全局最佳粒子为序号为14的乘车方案，即乘车方案为C-C-C-B-B、旅游总费用为498、旅游总时间为4.4、总满意度为41的乘车方案。

此外，由于不同的散客具有不同的条件、要求或感受，选择的旅游线路未必相同，如经济条件比较充裕且对费用不是很在意的散客可能会选择费用为501的乘车方案“C-C-C-C-C”，而对费用比较在意的可能会选择费用为258或270的乘车方案，但更多的散客可能会综合考虑费用、时间和满意度后再选择乘车方案。

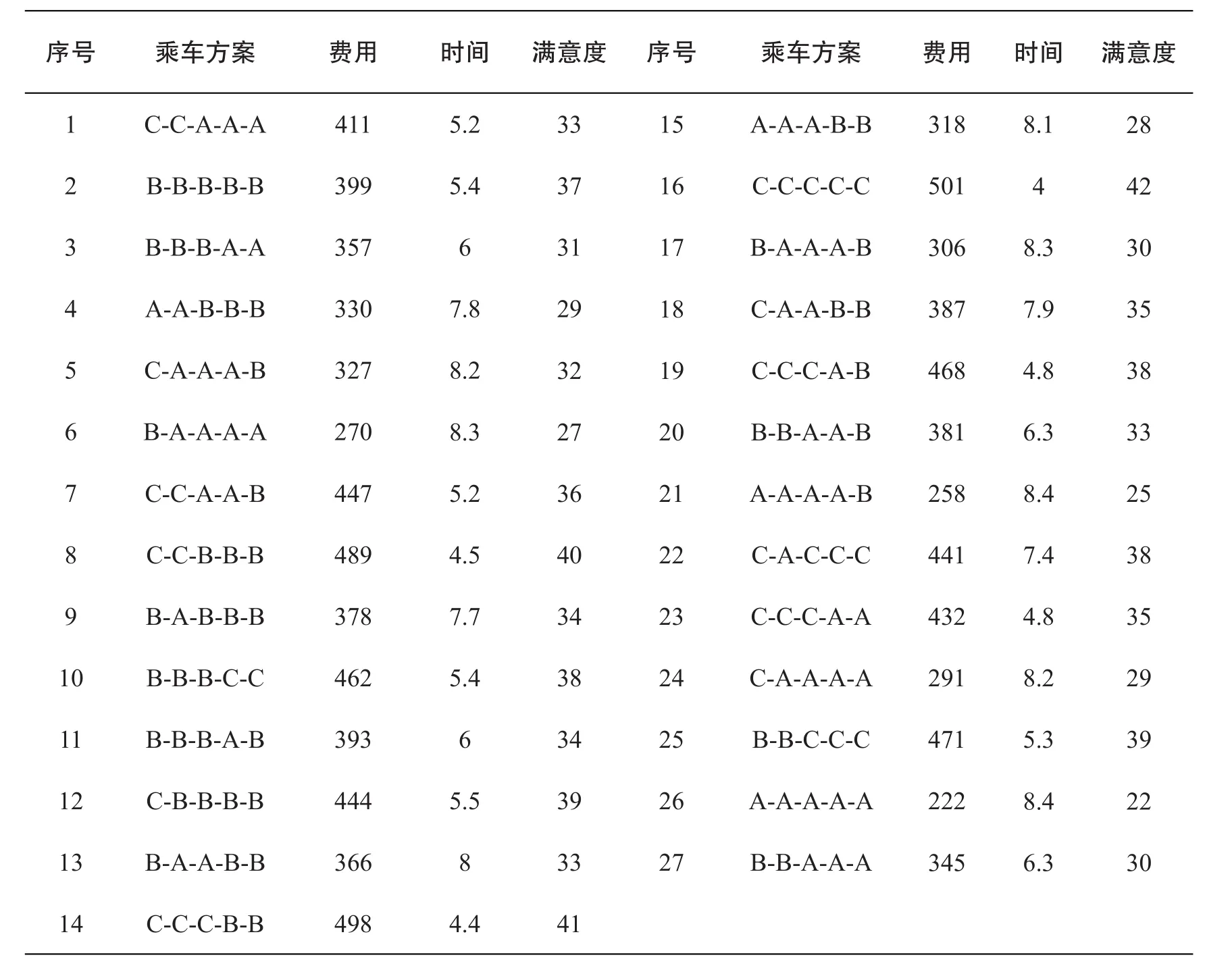
表3 粒子群算法求解的结果

如果旅游线路问题包含交通工具的运量限制，可以先将散客量与交通工具运量作比较，无法作业的交通工具所在路径预处理为此处不存在路径，再应用本文算法进行求解即可。当旅游线路途经的节点太多，加入虚拟节点的模型容易出现“组合爆炸”现象，用最短路算法求解未必理想，而本文算法易于理解、实现简单及效果显著，可以用来高效优化运输方案选择。对于本模型的改进，需要进一步考虑的问题是满意度的假设比较简单，后续研究可以扩展满意度的关联范围或测定，其次是求解多目标数学模型的方法的进一步扩展及实例的验证。