基于二部图最大匹配的动态负载均衡算法①

周 磊 孟利民 周立鹏 蒋 维

(*浙江工业大学信息工程学院 杭州 310023) (**浙江树人大学信息科技学院 杭州 310015)

0 引 言

随着网络技术的高速发展，互联网服务已经成为日常生活中不可或缺的部分。由于互联网用户的爆发式增长，服务器常常在短时间内收到大量并发的用户请求，若不能及时处理这些请求将影响用户体验，降低服务质量。因此，单个服务器远远无法满足大量的服务请求，联合多个服务器的服务器集群应运而生。如何合理地分配集群服务器的任务并满足最大的服务需求是服务器集群需要解决的关键技术问题，而负载均衡是解决服务器集群难点的核心技术之一，能够平衡集群中各个服务节点的负载，充分发挥服务器集群的性能。目前国内外已经提出了各种负载均衡算法[1]。其中有静态负载均衡算法，如轮询调度算法、加权轮询调度算法[2]、目标地址散列调度算法等，这类算法易于实现，但不考虑各个服务器节点的负载状态，容易导致负载不均衡；有动态负载均衡算法[3,4]，如最小连接数算法、一致性哈希算法[5]、动态反馈算法[6]等，这类算法没有考虑服务器间的性能差异和任务请求的大小，不能准确地判断服务器真实的负载状态。动态负载均衡算法注重于服务器负载状态的计算和反馈，文献[7]提出一种基于排队论综合指标评估的动态负载均衡算法，采用服务器M/M/1排队模型，以任务的平均排队时长和平均等待时长来计算负载，但其计算需花费较多时间，具有一定的延后性。文献[8]提出了一种改进的流媒体集群动态负载均衡调度算法，通过集群节点任务数变化量动态修改服务器负载的反馈周期，并按服务器负载状况进行分类，但当反馈周期过小时，服务器将频繁计算负载，增加服务器压力。在异构网络应用中，文献[9]提出了一种基于模糊控制的负载均衡决策机制，用于避免异构网络中频繁切换。文献[10]提出了一种基于接入选择和业务转移的异构网络动态负载均衡机制，同时提高系统利用率和负载均衡性。还有注重任务调度的遗传算法、模拟退火算法[11]、粒子群算法[12]等，这类算法实现较为复杂，且容易陷入局部最优解。文献[13]提出一种基于遗传算法的负载均衡机制，引入了投资组合Mean-Variance模型来设置服务集群中节点利用率的权重，以最小化任务完成时间为条件来获得最优的权值向量，即为每个服务器的资源利用率分配权值从而得到更有效的组合适应度函数，但其计算效率一般，对服务器的响应时间有一定的影响。

影响负载均衡算法性能的关键在于如何动态地将任务均衡地分配至各个服务器节点，因此本文提出了一种基于二部图最大匹配的动态负载均衡算法。二部图最大匹配[14]是指二部图中不相邻的边组成的集合中含边数最多的集合，常用于解决任务指派、资源分配[15]、数据匹配[16]等问题。在服务器集群系统中，管理服务器按照一定的机制将任务队列中的任务分配给集群中的各个服务器节点，这就是可用二部图最大匹配解决的现实应用场景之一。本文算法以服务器和任务作为图顶点的子集X和Y，先预计任务的任务量和期望完成任务所需的时间，并采用由服务器反馈得到的任务量与任务实际完成时间的比值作为服务器的负载指标[17]，若任务预计的任务量与服务器负载指标的比值小于期望完成任务所需的时间，则将该任务顶点与服务器顶点相连作为图的边，由此得到服务器与任务的二部图，再采用Edmonds的匈牙利算法[18]求该二部图的最大匹配，然后将任务发送给匹配到的服务器，从而动态地实现任务的调度和服务器的负载均衡。

1 负载均衡算法调度模型

本文提出的基于二部图最大匹配的动态负载均衡算法的系统框架如图1所示。整个系统主要由管理服务器和服务器集群组成。其中服务器集群中的服务器用于执行任务，并计算自身的负载指标返回给管理服务器。管理服务器可分为4个模块，分别是任务分配模块、任务预估模块、负载指标接收模块和计算模块。负载指标接收模块负责接收服务器反馈的负载指标，并更新当前保存在管理服务器的服务器集群负载信息。任务预估模块负责预计待匹配任务的任务量和期望完成任务所需的时间。计算模块根据各个服务器的负载指标以及任务的任务量和期望完成时间，构建服务器与任务之间的二部图并求其最大匹配。任务分配模块按照由计算模块返回的匹配结果将任务分配给各个服务器。

图1 基于二部图最大匹配的动态负载均衡算法系统框架

服务器每执行一个任务，将记录该任务的任务量r，任务开始时间tstart和任务完成时间tend，并由式(1)得到服务器当前负载指标v。

(1)

服务器负载指标代表服务器完成任务的速率，与常见算法采用中央处理器(CPU)空闲率、内存空闲率等多参数计算负载指标相比，降低了服务器负载计算的复杂度，且更直接地反映了当前服务器的负载状态。若v越大，则说明服务器的负载较低，能更快地完成任务；若v越小，则说明服务器的负载较大，完成任务需要消耗更多的时间。那么服务器集群的负载指标平均值为

(2)

其中，n为集群中服务器数量。由此可以得到各个服务器负载指标的方差σ2：

(3)

方差σ2越小，说明服务器之间的负载越均衡。

2 负载均衡算法流程

本文算法是基于任务队列、服务器集群和各服务器负载指标构建二部图，并根据二部图的最大匹配结果向各服务器分配任务，其总体流程图如图2所示。

图2 算法流程图

整个算法流程主要由管理服务器和服务器集群共同工作完成。首先管理服务器中维护着一个任务队列，任务队列中含有一定量待执行的任务，由集合表示为Jq={J1,J2,J3,…}。服务器集群中有n台服务器，由集合表示为S={S1,S2,S3,…,Sn}，服务器Si主要负责接收并执行管理服务器为其分配的任务Jm。服务器Si将在任务Jm被执行前后记录该任务的任务量Rm，以及执行任务的开始时间Tmstart和结束时间Tmend，同时由式(1)计算得到当前服务器Si的负载指标vi，并将负载指标vi反馈至管理服务器。

管理服务器的负载指标接收模块中记录着服务器集群中各个服务器的负载指标，由集合表示为v={v1,v2,v3,…,vn}。各个服务器的初始化负载指标可通过管理服务器向各个服务器发送一个测试任务J0获得，其任务量为单位任务量R0，任务复杂度为C0，任务复杂度与任务实际计算循环次数相关。

管理服务器记录各个服务器的初始化负载指标后，从任务队列中按顺序取出与服务器数量相等的n个任务，由集合表示为J={J1,J2,J3,…,Jn}，同时通过任务预估模块得到对应任务的任务量为R={R1,R2,R3,…,Rn}，期望完成任务所需时间为T={T1,T2,T3,…,Tn}。那么对于任务Jm，其任务量Rm可由式(4)得到：

(4)

其中，R0为单位任务量，C0为测试任务的复杂度，Cm为任务Jm的复杂度。任务Jm的期望完成时间Tm可由式(5)得到：

(5)

其中，T0为测试任务实际运行时间，α的取值为经验值。

管理服务器通过任务预估模块得到任务量R和期望完成任务所需时间为T后，根据实时记录的服务器负载指标v，开始构建二部图。一般的图可由G={V,E}表示，其中V为图G的顶点集合，E为图G的边集合，由此管理服务器以服务器集合S和任务集合J作为图的顶点集可得无边图G，如图3所示，显然V=S∪J，E=Ø。

然后管理服务器对所有服务器和任务进行遍历，对于任意一个服务器Si和一个任务Jm，可由式(6)预估服务器Si、执行任务Jm、实际所需时间tim：

图3 以集合S和集合J为顶点的无边图G

(6)

若tim≤Tm，则表示服务器Si能够胜任任务Jm的工作，即预计服务器Si能在任务Jm的期望时间Tm内完成该任务，并将图G中的顶点Si和顶点Jm相连，得到一条边e=SiJm，将e加入图G的边集合中，即E=E∪e；若tim>Tm，则表示以服务器Si当前的负载状态无法及时地完成任务，那么图G中的顶点Si和顶点Jm不相连。上述遍历完成后即可得到服务器S与任务J的二部图G，如图4所示。对于服务器Si，若与之相连的顶点较多，表示当前该服务器负载较低，能胜任较多的任务；若与之相连的顶点较少，表示当前该服务器负载较高，只能胜任部分任务；若没有与之相连的顶点，表示当前该服务器负载较高，暂时不接收任务。

图4 服务器S与任务J的二部图G

管理服务器得到二部图G后，根据深度优先的Edmonds的匈牙利算法求二部图G的最大匹配。遍历顶点集合S，使顶点Si依次与集合J中的顶点进行匹配，若顶点Si与顶点Jm相连，且顶点Jm还未与集合S中的其他顶点匹配，则边e=SiJm为一条匹配边，并开始匹配集合S的下个顶点；若顶点Si与顶点Jm相连，但顶点Jm已经与集合S中的其他顶点匹配，则寻找其増广路，若找到増广路，则将増广路的匹配边变成未匹配边，而未匹配边变成匹配边，例如找到一条増广路Si-J1-S1-Ji，则该増广路匹配边S1J1变成未匹配边，未匹配边SiJ1和S1Ji变成匹配边，并开始匹配集合S的下个顶点；若找不到増广路，则顶点Si没有匹配边。集合S遍历完后，所有匹配边的集合即为二部图G的最大匹配M={SiJm,…}。对于M中的匹配边SiJm，表示以服务器Si当前的负载状况能胜任任务Jm。

管理服务器得到构建的二部图G的最大匹配M后，由任务分配模块按照M中的匹配边SiJm，将任务Jm发送至服务器Si进行执行。若任务集合J中存在没有匹配边的任务，则将该任务移至任务队列队首，重新进行二部图构建和求最大匹配流程。

在整个算法流程中，构建二部图需要对每个服务器与每个任务之间进行判断，因此对于n个服务器和n个任务，其时间复杂度为O(n2)。对二部图最大匹配采用深度优先匈牙利算法求解时，二部图一边有n个点，最多找到n条増广路，若二部图构建完成后有x条边，那么每条増广路把所有边遍历一遍，其时间复杂度为O(nx)。而根据二部图构建流程，二部图中最多存在n2条边，因此最坏时间复杂度为O(n3)，所以整个算法流程的最高时间复杂度为O(n3)。由于服务器集群的应用场景中服务器个数主要为一位数或两位数，所以管理服务器能很快计算出最大匹配。

重复上述算法流程，管理服务器即可将任务队列中的任务分配至各个服务器中执行，同时低负载的服务器更容易匹配到任务量较大且期望时间较短的任务，高负载的服务器更容易匹配到任务量小且期望时间较长的任务，甚至不会匹配到任务，由此可以实现任务并发时服务器集群中各服务器间的负载均衡。

3 算法仿真与性能分析

本文采用Java语言编写管理服务器和服务器集群的程序，系统采用1个管理服务器和4个服务器组成的服务器集群，服务器配置参数如表1所示。

表1 服务器配置

基于本文算法，通过向管理服务器分别发送500、1 000、1 500个任务的任务队列，运行20 s后每隔5 s记录服务器的负载指标，比较不同取值对本文算法的影响，结果如图5所示。由图5可知，当向管理服务器发送500个任务时，α取0.667的负载指标方差大部分时间都低于其他取值的负载指标方差；当向管理服务器发送1 000个任务时，α取0.667的负载指标方差大部分时间都低于或接近其他取值的负载指标方差；当向管理服务器发送1 500个任务时，20～50 s内4种取值的负载指标方差都变化较大，50 s后α取0.667和0.833的大部分时间都低于其他取值的负载指标方差。

服务器分别完成500、1 000、1 500个任务所消耗的时间如表2所示。由表2可知，当α取0.667时，服务器完成所有任务消耗时间较少。综合图5和表2，当本文算法的α值取0.667时，服务器拥有较好的负载均衡度，且完成任务消耗时间较少。

表2 不同α值服务器完成任务消耗时间

以下实验本文算法的α值均取0.667。通过向管理服务器发送500、1 000、1 500个任务的任务队列，对常见的加权轮询调度算法、最小连接数算法和

(a) 500个任务

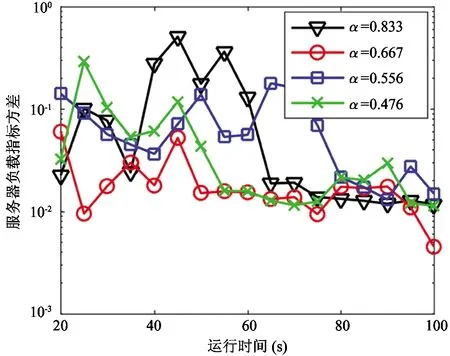
(b) 1 000个任务

基于排队论综合指标评估的动态负载均衡算法(以下简称排队论算法)与本文算法进行仿真分析，运行20 s后每隔5 s记录服务器的负载指标，通过负载指标的方差评估服务器的负载均衡情况，实验结果如图6所示。由图6可知，在3个不同任务队列的情况下，运行20 s后本文算法负载指标的方差大部分时间都低于加权轮询调度算法、最小连接数算法和排队论算法，说明采用本文算法的服务器集群负载均衡度更好。

(a) 500个任务

(b) 1 000个任务

(c) 1 500个任务

3种算法完成500、1 000、1 500个任务所消耗的时间如表3所示。根据表3数据，当任务数量较少时，由于加权轮询算法未考虑服务器实时的负载状态，最小连接数算法和本文算法均优于加权轮询算法，但此时本文算法和最小连接数算法差距不大；当任务数量逐渐增大时，本文算法逐渐优于最小连接数算法，消耗的时间更少。

表3 完成队列所有任务消耗的时间

4 结 论

针对服务器集群系统中管理服务器调度任务的场景，本文提出了一种基于二部图最大匹配的动态负载均衡算法，以二部图的匹配结果作为管理服务器的调度方案。仿真实验结果表明，该算法与加权轮询调度算法、最小连接数算法和基于排队论综合指标评估的动态负载均衡算法相比，能使服务器拥有更好的负载均衡度；而且对于相同数量的任务队列，采用该算法的服务器集群能更快地完成所有任务。

由于通过二部图求出的最大匹配不一定是完美匹配，于是就存在取出的任务未匹配到服务器的情况，本文算法将该任务放回任务队列，容易导致该任务的响应时间过长，今后可以在这类任务的处理上对算法进行改进和优化；本文算法求解二部图最大匹配的计算复杂度与服务器数量相关，当服务器规模较大时，算法效率将下降，因此对求二部图最大匹配的匈牙利算法的改进也是本文算法的重要优化方向之一。